 |
Графики функций двух переменных
|
|
|
|
Для отображения функций двух переменных следует:
1. Сгенерировать матрицы с координатами узлов сетки на прямоугольной области определения функции.
2. Вычислить функцию в узлах сетки и записать полученные значения в матрицу.
3. Использовать одну из графических функций MatLab.
4. Нанесение на график дополнительной информации.
Сетка генерируется при помощи команды meshgrid, вызываемой с двумя переменными. Аргументами являются векторы, элементы которых соответствуют сетке на прямоугольной области построения функции (если область квадрат, то используется один аргумент).
Например: Построим график функции  на прямоугольной области определения хÎ[-1; 1], yÎ[0; 1].
на прямоугольной области определения хÎ[-1; 1], yÎ[0; 1].
Сначала подготовим с координатами узлов сетки и значениями функции:
>> [x, y]= meshgrid(-1:0.05:1, 0:0.05:1);
>>z=4*sin(2*pi*x).*cos(1.5*pi*y);
Для построения каркасной поверхности, используется функция mesh, вызываемая с тремя аргументами:
>> mesh (x, y, z)
Кроме этого, существуют несколько команд, которые меняют внешний вид графика:
hidden off – делает каркасную поверхность «прозрачной», добавив скрытую часть;
hidden on – возвращает графику прежний вид;
shading flat – убирает каркасные линии;
shading interp – получает поверхность, плавно залитой цветом, зависящим от значений функций.
Вычисление всех корней полинома
Полином в MatLab задается вектором его коэффициентов. Например, для определения полинома  следует использовать команду
следует использовать команду
>> p=[1 0 3.2 -5.2 0 0.5 1 -3];
Число элементов вектора, т.е. число коэффициентов полинома, всегда на единицу больше его степени, нулевые коэффициенты должны содержаться в векторе.
Функция polyval предназначена для вычисления значения полинома от некоторого аргумента:
>> polyval(p,1)
|
|
|
ans=
-2.5000
Нахождение всех корней полиномов осуществляется при помощи функции roots, в качестве аргумента которой указывается вектор с коэффициентами полинома. Функция roots возвращает вектор корней полинома.
Задание символьных переменных
Поскольку переменные системы Matlab по умолчанию не определены и традиционно задаются как векторные, матричные, числовые и т. д., то есть не имеющие отношения к символьной математике, для реализации символьных вычислений нужно создать специальные символьные переменные. В простейшем случае их можно определить как строковые переменные, заключив имена в апострофы.
Пример: Сумма квадратов синуса и косинуса переменной ‘x’ равна 1.
>> sin(‘x’)^2+cos(‘x’)^2
ans =
Для создания символьных переменных или объектов используется функция sym:
• S = sym (А) - возвращает символьный объект S класса 'sym' для входного параметра А. Если А — строка, то будет получена символьная строка или символьная переменная, а если А — это число (скаляр) или матрица, то будут получены их символьные представления;
• х = sym('x') — возвращает символьную переменную с именем 'х'.
Для создания группы символьных объектов служит функция syms:
• syms argl arg2... — создает группу символьных объектов, подобную выражениям
argl = sym('argl'); arg2 = sym('arg2');
• syms argl arg2... real и syms argl arg2... unreal — создают группы символьных объектов с вещественными (real) и невещественными (unreal) значениями. Последнюю функцию можно использовать для отмены задания вещественности объектов.
Вычисление производных
Для вычисления в символьном виде производных от выражения S служит функция dif f, записываемая в формате dif f (S, 'v') или dif f (S, sym(' v')). Она возвращает символьное значение первой (n=1) производной от символьного выражения или массива символьных выражений S по переменной v. Эта функция возвращает  .
.
• diff (S, n) — возвращает n-ю (n — целое число) производную от символьного выражения или массива символьных выражений S по переменной V.
|
|
|
• diff (S, ' v', n) и diff(S,n,'v') —возвращает n-ю производную S no переменной v, то есть значение 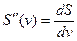 .
.
Пример:
>> x=sym(‘x’); y=sym(‘y’);
>> diff(x^y)
ans=
x^y*y/x
Вычисление интегралов
В практической работе часто возникает необходимость вычисления неопределенных и определенных интегралов вида  и
и  .
.
Здесь f(x) — подынтегральная функция независимой переменной х, а - нижний и b - верхний пределы интегрирования для определенного интеграла.
• int(S) - возвращает символьное значение неопределенного интеграла от символьного выражения или массива символьных выражений S по переменной, которая автоматически определяется функцией findsym. Если S - скаляр или матрица, то вычисляется интеграл по переменной 'х'.
• int (S, v) — возвращает неопределенный интеграл от S по переменной v.
• int (S, a, b) — возвращает определенный интеграл от S с пределами интегрирования от а до b, причем пределы интегрирования могут быть как символьными, так и числовыми.
• int(S,v,a,b) — возвращает определенный интеграл от S по переменной v с пределами от а до b.
Пример:
>> x=sym(‘x’); y=sym(‘y’);
>> int(x^2, x)
ans=
1/3*x^3
Вычисление пределов
Вычисление пределов функций представляет собой важный раздел математического анализа.
Для вычисления пределов аналитически (символьно) заданной функции F(x) служит функция limit, которая записывается в следующих вариантах:
• limit (F, х, а) — возвращает предел символьного выражения F в точке х®а;
• limit (F, a) — возвращает предел для независимой переменной, определяемой функцией findsym;
• limit (F) — возвращает предел при а=0;
• limit (F, х, а, 'right') или limit (F,x, a, 'left') —возвращает предел в точке а справа или слева.
Пример:
>> syms a x
>> limit(sin(a*x)/(a*x))
ans=
|
|
|


