 |
Метод Зейделя. Условие сходимости
|
|
|
|
Погрешность степени
Предельная относительная погрешность m-ой степени в m раз больше предельной относительной погрешности подкоренного числа.
δu=m·δx
Погрешность корня
Предельная относительная погрешность корня m-ой степени в m раз меньше предельной относительной погрешности подкоренного числа.
δu=(1/m)·δx
9) Системы линейных уравнений(СЛУ)
Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
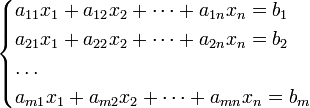
| (1) |
Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы; b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
Система линейных уравнений может быть представлена в матричной форме как:

или:
A x = B.
Если к матрице А приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
|
|
|
10) Решение произ. линейного уравнения
Система m уравнений с n неизвестными в общем виде записывается следующим образом:
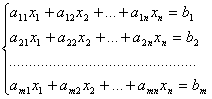
где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.
Правило решения:
1. Найти ранги основной и расширенной матриц системы. Если r(A)≠r(A), то система несовместна.
2. Если r(A)=r(A)=r, система совместна. Найти какой-либо базисный минор порядка r (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные n-r неизвестных называют свободными и переносят в правые части уравнений.
3. Найти выражения главных неизвестных через свободные. Получено общее решение системы.
4. Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образом можно найти частные решения исходной системы уравнений.
11) Однородная СЛУ
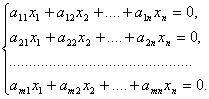 (7.1).
(7.1).
Однородная система всегда совместна, так как всегда имеется тривиальное решение.
Согласно общей теории, если r(A)=n, то единственным является тривиальное решение.
Если же r(a)<n, то решений бесконечно много, и все они, кроме одного, нетривиальные.
Теорема 1 (о нетривиальных решениях однородной системы)
Однородная линейная система с квадратной матрицей имеет нетривиальное решение тогда и только тогда, когда определитель системы равен нулю.
Определение 1
Всякая линейно независимая система
(n-r) решений системы линейных однородных уравнений называется фундаментальной системой решений.
Замечание 1. Отличный от нуля минор матрицы порядка r, такой, что всякие миноры порядка r+1 и выше, (если такие имеются) равны нулю, называется базисом.
|
|
|
12) Метод Гаусса
Рассмотрим систему линейных уравнений S. Метод Гаусса решения систем линейных уравнений состоит из двух этапов, называемых прямым и обратным ходом. Прямой ход метода Гаусса заключается в том, что с помощью элементарных преобразований над расширенной матрицей система S приводится к «ступенчатому» виду.
Обратный ход метода Гаусса состоит в том, что, начиная с последнего уравнения ступенчатой системы, вычисляются неизвестные.
При реализации прямого хода метода Гаусса возможны следующие три случая.
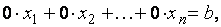 В результате преобразований в системе уравнений будет получено уравнение вида
В результате преобразований в системе уравнений будет получено уравнение вида
где b≠0. Ясно, что никакой набор действительных чисел этому уравнению удовлетворять не может, поэтому в таком случае система уравнений несовместна.
2. В результате преобразований получится ступенчатая система уравнений

в которой количество уравнений совпадает с количеством неизвестных.
В этом случае система уравнений является определённой.
3.В результате преобразований получится система уравнений ступенчатого вида, в которой количество неизвестных больше числа уравнений системы (m>n)

В этом случае те неизвестные, которые стоят на «ступеньках», называются главными неизвестными (x1,x2,…..,xm), а другие неизвестные называются свободными (xm+1,xm+2,….,xn); система уравнений будет неопределённой. Тогда обратный ход метода Гаусса состоит в том, что начиная с последнего уравнения системы, главные неизвестные выражаются через свободные и составляется общее решение системы уравнений. Для того чтобы получить какое-либо частное решение системы, свободным неизвестным придают конкретные числовые значения, вычисляя тем самым главные неизвестные.
13) Метод итераций
Метод простой итерации (метод последовательных повторений).Для применения метода простой итерации следует исходное уравнение 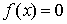
преобразовать к виду, удобному для итерации 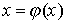 . Это преобразование можно выполнить различными способами. Функция
. Это преобразование можно выполнить различными способами. Функция 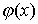 называется итерационной функцией. Расчетная формула метода простой итерации имеет вид:
называется итерационной функцией. Расчетная формула метода простой итерации имеет вид: 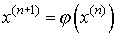 .
.
|
|
|
14) Условия сходимости итерационного процесса
15) Оценка погрешности в методе итерации
Теорема о сходимости метода простой итерации. Пусть в некоторой 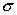 - окрестности корня
- окрестности корня  функция
функция 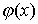 дифференцируема и удовлетворяет неравенству
дифференцируема и удовлетворяет неравенству 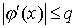 , где
, где 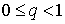 - постоянная. Тогда независимо от выбора начального приближения из указанной
- постоянная. Тогда независимо от выбора начального приближения из указанной 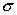 - окрестности итерационная последовательность не выходит из этой окрестности, метод сходится
- окрестности итерационная последовательность не выходит из этой окрестности, метод сходится
со скоростью геометрической последовательности и справедлива оценка погрешности: 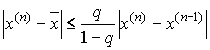 ,
, 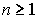 .
.
Метод Зейделя. Условие сходимости
Решение системы Ax=U по методу Зейделя производится по формулам
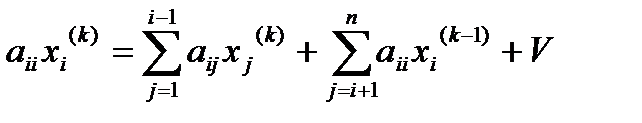
Если при вычислении i-той координаты вектора

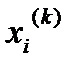 учитывается найденные заранее уже координаты
учитывается найденные заранее уже координаты 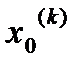
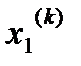 …
… 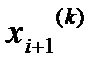
То вычисления будут проходить по формулам Зейделя.
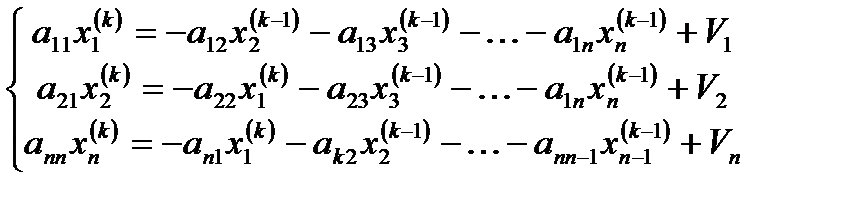
|
|
|


