 |
Метод Горнера уточнения действительных корней
|
|
|
|
Схема Горнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов, при заданном значении переменной. Метод Горнера позволяет найти корни многочлена, а также вычислить производные полинома в заданной точке. Схема Горнера также является простым алгоритмом для деления многочлена на бином вида x − c.
При делении многочлена
на x − c получается многочлен
с остатком bn.
При этом коэффициенты результирующего многочлена удовлетворяют рекуррентным соотношениям:
b0 = a0, bk = ak + cbk − 1.
Таким же образом можно определить кратность корня (использовать схему Горнера для нового полинома). Так же схему можно использовать для нахождения коэффициентов при разложении полинома по степеням x - c: 
Нахождение границ корней
Для многочлена 
1) верхняя граница модулей корней - число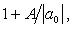 
где 
2) верхняя граница положительных корней – число
где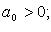 
B - наибольшее число из модулей отрицательных коэффициентов; k - номер первого из отрицательных коэффициентов;
3) нижняя граница положительных корней - число 
где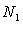 
- верхняя граница положительных корней многочлена 
4) верхняя граница отрицательных корней - число - 
где 
- верхняя граница положительных корней многочлена 
5) нижняя граница отрицательных корней - число - 
где - верхняя граница положительных корней многочлена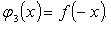 
Метод Штурма
Изменить 2 переменные так, чтобы из одной части неравенства получилась другая и вдобавок к этому всегда изменяемая часть изменялась в одну, нужную нам, сторону (или увеличивалась либо уменьшалась). Обычно этого можно достичь, изменяя 2 числа с постоянно суммой или произведением
Функции и её способы задания
|
|
|
Функция — математическое понятие, отражающее связь между элементами различных множеств. Более точно, это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.
Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность.
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.
Основные понятия теории приближения функции
Постановка задачи приближения функции по методу наименьших квадратов. Пусть функция y=f(x) задана таблицей своих значений: 
, i =0,1,- n. Требуется найти многочлен фиксированной степени m, для которого среднеквадратичное отклонение
минимально. Так как многочлен
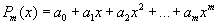определяется своими коэффициентами, то фактически нужно подобрать набор коэффициентов 
, минимизирующий функцию
.
Используя необходимое условие экстремума, 
, k =0,1,- m получаем так называемую нормальную систему метода наименьших квадратов: 
, k =0,1,- m.
Полученная система есть система алгебраических уравнений относительно неизвестных . Можно показать, что определитель этой системы отличен от нуля, то есть решение существует и единственно. Однако при высоких степенях m система является плохо обусловленной. Поэтому метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5.
|
|
|
|
|
|
