Построение системы нормальных уравнений. Оценка коэффициентов уравнения множественной регрессии

Оцененное уравнение в первую очередь должно описывать общий тренд (направление) изменения зависимой переменной Y. При этом необходимо иметь возможность рассчитать отклонения от этого тренда.

По данным выборки объема n: (x_1i, x_2i,..., х_pi, у_i), i = 1,2,..., n, требуется оценить значения параметров b_i вектора b, т.е. оценить (приблизить) значения коэффициентов выбранной обычно вначале линейной модели (здесь х_ij, (j = 1, 2,..., n) - это значение переменной X_i в j-ом наблюдении).

y_i = b₀ + b₁×x_1i + b₂×x_2i +…+ b_p×x_pi+ e_i.. (5.2)

При выполнении предпосылок МНК (о них мы поговорим позже) относительно ошибок е_i оценки b₀, b₁, …, b_p коэффициентов b₀, b₁,..., b_p множественной линейной регрессии по МНК являются несмещенными, эффективными и состоятельными.

На основании (5.2) отклонение e_i значения у_i зависимой переменной Y от теоретического (модельного) значения

у_teor(x_1i, x_2i,..., х_pi) = b₀ + b₁×x_1i + b₂×x_2i +…+ b_p×x_pi (5.3)

соответствующего уравнению регрессии в i-м наблюдении (i = 1, 2,..., n), рассчитывается по формуле

e_i = y_i - b₀ - b₁×x_1i - b₂×x_2i -…- b_p×x_pi.

Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК), т.е. минимизируется функция S(b₀, b₁,…, b_p) по переменным b₀, b₁,…, b_p

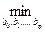S(b₀, b₁,…, b_p) = . (5.3')

На основании необходимого условия экстремума функции многих переменных S(b₀, b₁,..., b_p), представляющей (5.3'), необходимо приравнять к нулю частные производные по этим переменным или в матричной форме — вектор частных производных

.

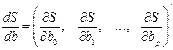В результате получится система p+1 линейных уравнений для неизвестных b₀, b₁,..., b_p. После приведения подобных членов получится система нормальных уравнений, решение которой и позволяет получить оценку коэффициентов множественной регрессии.

Так для уравнения y_teor(x_1i, x_2i,..., х_pi) = b₀+b₁×x_1i + b₂×x_2i +…+ b_p×x_pi система нормальных уравнений имеет вид:

Ее решение может быть найдено в частности, методом Гаусса, методом Крамера, методом вычисления обратной матрицы и многими другими методами решения систем линейных уравнений.

В пункте 5.3 будет показано, как обратиться к процедурам в Microsoft Excel, позволяющим решать это уравнение и вычислять не только значения коэффициентов множественной регрессии, но и числовые значения других ее характеристик.

При нелинейной зависимости признаков, приводимой к линейному виду, значения коэффициентов множественной регрессии также определяются также с помощью метода наименьших квадратов лишь с той разницей, что он применяется не к исходной информации, а к преобразованным данным. Так, рассматривая степенную функцию

мы преобразовываем её в линейный вид:

ln(y) = ln(a) + b1×ln(x₁) + b2×ln(x₂) + … + bp×ln(x_p) + ln(e),

где переменные выражены в логарифмах.

Далее метод наименьших квадратов применяется так же, как и раньше: строится система нормальных уравнений и определяются значения ln(a), b1, b2, …, bp. Потенцируя ln(a), найдём значение параметра а и общий вид уравнения степенной функции.

Поскольку параметры степенной функции представляют собой коэффициенты эластичности, то они сравнимы по разным факторам.

Пример 2. При исследовании спроса на некоторый продукт получено следующее уравнение

ln(y) = -1,28 – 0,888×ln(x₁) + 1,126×ln(x₂) + e,

где у – количество продукта на душу населения (кг); х₁ – цена (руб.); х₂ – доход на душу населения (тыс. руб.)

Из этого уравнения видно, что с ростом цены на 1% при том же доходе спрос снижается в среднем на 0,888%, а увеличение дохода на 1% при неизменных ценах вызывает увеличение спроса на 1,126%.

При других нелинейных функциях методика оценки параметров метода наименьших квадратов выполняется также. В отличие от предыдущих функций параметры более сложных моделей не имеют чёткой экономической интерпретации – они не являются показателями силы связи и её эластичности. Это не исключает возможности их применения, но делает их менее привлекательными в практических расчётах.