Задание к лабораторной работе №3 «Множественная линейная регрессия»

 

Задание. Построить множественную линейную модель связи между указанными факторами, осуществить точечный прогноз. Исходные данные находятся в таблице 1.

Методические указания к решению задачи.

1. Вначале расположите исходные данные по факторам X₁, X₂, …, X_k и Y в столбцы.

Полагая, что связь между факторами X₁, X₂, …, X_k и Y может быть описана линейной функцией, запишите соответствующее уравнение этой зависимости. Используя процедуру метода наименьших квадратов, получите систему нормальных уравнений относительно коэффициентов линейного уравнения регрессии. С помощью вычисления обратной матрицы решите ее. Проверьте полученные оценки описанным выше способом в MS EXCEL.

3. Выполните точечный прогноз на прогнозное значение х_п переменных x₁, x₂,…x_k по полученной модели. Выберите прогнозную точку х_п в стороне от основного массива данных. Используя уравнение регрессии, выполните точечный прогноз величины Y в точке х_п.

4. Для полученной модели связи между факторами X₁, X₂, …, X_k и Y найдите рассчитанные значения коэффициента детерминации R², коэффициента Фишера F. Сделайте предварительное заключение о приемлемости полученной модели.

 

Вариант 1. Требуется построить статистическую зависимость стоимости квартиры от трёх факторов в виде множественной регрессии. Оцените полученную модель с помощью коэффициента детерминации R² и с помощью t-критерия Стьюдента, оценивающего значимость каждого коэффициента множественной регрессии.

Таблица 1

№ изм.	Общая площадь, м2, X1	Жилая площадь квартиры,м2, Х2	Расстояние до метро, минут пешком, Х3	Стоимость квартиры, тыс. дол., Y
	69,7
		80,3		19,8
	96,4
				24,8
				27,3
		86,8
	114,8
	114,3	74,7		38,6
		78,8		42,7
		69,4
		72,8		23,8
		73,7		48,8
		61,7
		48,8
	74,7	80,8		26,8
		79,8

 

По данным таблицы 1 выполните следующие шаги.

Шаг 1. Вычислите коэффициенты множественной регрессии методом наименьших квадратов с помощью Сервис, Анализ данных, Регрессия.

Шаг 2. Вычислите матрицу А и столбец d правых частей системы нормальных уравнений

 

(5.11)

на основе составления на листе MS EXCEL массивов. Вначале дополните таблицу 1 единицами и образуйте массив (матрицу плана)

.

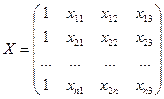Пусть он расположен, например, в блоке F1:I4. Поставьте курсор на чистую ячейку и с помощью команд: f_x, ссылки и массивы, ТРАНСП(F1:I4), транспонируйте массив X. Получим одно число (равное 1) в этой чистой ячейке. Поскольку матрица, транспонированная к матрице размерности 4х4, тоже будет иметь размерность 4х4, это число является тем числом, которое стоит в левом верхнем углу этой матрицы. Для того чтобы отобразить оставшиеся числа матрицы, нужно выделить левой кнопкой мыши оставшиеся 15 клеток, чтобы выделилась матрица 4х4, а затем нужно нажать на клавиши F2, CTRL+SHIFT+ENTER.

Теперь в вашем распоряжении имеется матрица X и транспонированная к ней матрица X', расположенная например, в блоке K1:N4. Ставим курсор на чистую ячейку. Например, К11.

.

Вычисляем матрицу А = X'X с помощью команд

f_x, математические, МУМНОЖ(F1:I4; K1:N4).

Получим одно число в этой чистой ячейке. Поскольку если матрицу размерности 4х4 умножить на такую же матрицу 4х4, то получим тоже матрицу размерности 4х4, значит, это число является тем числом, которое стоит в левом верхнем углу этой матрицы. Для того чтобы отобразить оставшиеся числа матрицы, нужно выделить левой кнопкой мыши оставшиеся 15 клеток, чтобы выделилась матрица 4х4, а затем нужно нажать на клавиши F2, CTRL+SHIFT+ENTER.

Шаг 2. Как было отмечено ранее, решить систему нормальных уравнений можно разными методами, в частности, методом Гаусса, методом Крамера или вычислением обратной матрицы.

Рассмотрим, как это решается в MS EXCEL с помощью вычисления обратной матрицы. Далее вычислим обратную матрицу к матрице А. Для этого поставим курсор на чистую ячейку листа MS EXCEL (например, F21) и обращаемся к стандартной процедуре

f_x, математические, МОБР(K11:N14).

Получим одно число в этой чистой ячейке. Поскольку матрица, обратная к матрице размерности 4х4, тоже будет иметь размерность 4х4, это число является тем числом, которое стоит в левом верхнем углу этой матрицы. Для того чтобы отобразить оставшиеся числа матрицы нужно выделить левой кнопкой мыши оставшиеся 15 клеток, чтобы выделилась матрица 4х4, а затем нужно нажать на клавиши F2, CTRL+SHIFT+ENTER.

Теперь в вашем распоряжении имеется вся обратная матрица А^-1 размерности 4х4, расположенная, например, в блоке F21:I24.

Шаг 3. Вектор правых частей d

,

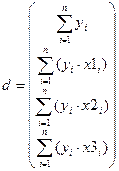вычислите как произведение матриц с помощью МУМНОЖ(;)

.

Для того чтобы получить неизвестные коэффициенты регрессии, необходимо умножить левую и правую части уравнения (2) на обратную матрицу. Получим

 

.

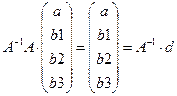Как видно из последнего уравнения, осталось умножить обратную матрицу на столбец d. В MS EXCEL это вычисляется следующим образом: ставим опять курсор на чистую ячейку листа MS EXCEL и обращаемся к стандартной процедуре

f_x, математические, МУМНОЖ(F21:I24; C11:I14).

Получим одно число в этой чистой ячейке. Поскольку если матрицу размерности 4х4 умножим на вектор, имеющий 4 координаты, получим тоже вектор, имеющий 4 координаты, то это число является тем числом, которое стоит в левом верхнем углу этого вектора. Для того, чтобы отобразить оставшиеся числа вектора, нужно выделить левой кнопкой мыши оставшиеся 3 клетки, чтобы выделился вектор размерности 4, а затем нужно нажать на клавиши

F2, CTRL+SHIFT+ENTER.

Теперь мы имеем вектор, координатами являются коэффициенты уравнения множественной регрессии.

Шаг 4. Сравните полученные значения коэффициентов с тем, что получены с помощью Сервис, Анализ данных, Регрессия. Вычислите сумму квадратов отклонений, объясненных регрессией SS_регр. и остаточную сумму квадратов отклонений SS_ост, а также дисперсию, объясненную регрессией MS_регр.= SS_регр./m и остаточную дисперсию MS_ост.= SS_ост./(n-m-1). Наконец, осталось вычислить выборочное (факторное) значение F-критерия F_факт. = MS_регр./MS_ост. Чтобы проверить правильность полученных вами значений, взгляните на полученный лист MS EXCEL на шаге 1. Все эти данные приведены на этом листе во втором блоке результатов под названием «Дисперсионный анализ».

 

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: