 |
Понятия о случайных событиях и о вероятности возникновения события
|
|
|
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ВОДНЫХ КОММУНИКАЦИЙ»
А. В. Одерышев
ОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ
Рекомендовано Редакционно-издательским советом
Санкт-Петербургского государственного университета водных
коммуникаций
Санкт-Петербург
УДК 642.014
ББК 38.54
Рецензент
Кандидат технических наук, доцент
Е. В. Матвеева
Одерышев А. В.
Основы научных исследований: учебно-методическое пособие по выполнению расчетной работы №2 «Мысленный эксперимент. Построение дерева исходов».— СПб.: СПГУВК, 2011 — 17 с.
Учебно-методическое пособие предназначено для студентов специальности 190600.62 «Эксплуатация транспортно-технологических машин и комплексов» по профилю «Эксплуатация перегрузочного оборудования портов и транспортных терминалов», изучающих дисциплину «Основы научных исследований».
В пособии дается понятийный аппарат научного эксперимента, приводятся основные сведения теории надежности, дается понятие о случайных событиях и их вероятностях, рассмотрена методика построения дерева исходов.
УДК 624.014
ББК 38.54
ã Одерышев А. В., 2011
ã Санкт-Петербургский государственный
университет водных коммуникаций, 2011
ОГЛАВЛЕНИЕ
1. ОБЩИЕ СВЕДЕНИЯ.. 4
1.1 Устройство козлового крана. 4
1.2 Понятия о случайных событиях и о вероятности возникновения события 5
1.3 Краткие сведения из теории надежности. 6
1.4 Мысленный эксперимент и построение дерева исходов. 8
|
|
|
2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ... 10
2.1 Исходные положения. 10
2.2 Порядок выполнения работы.. 10
2.3 Оформление отчета. 12
КОНТРОЛЬНЫЕ ВОПРОСЫ... 14
СПИСОК ЛИТЕРАТУРЫ... 15
ПРИЛОЖЕНИЕ 1. 16
Расчетно-практическая работа № 2: «Мысленный эксперимент. Построение дерева исходов»
ОБЩИЕ СВЕДЕНИЯ
Устройство козлового крана
Козловые краны (рис. 1) представляют собой сооружения, у которых горизонтальное пролетное строение (мост, 1) опирается на две опоры* (ноги, 2), перемещающиеся по наземным рельсовым путям (3), которые ограничены тупиковыми упорами кранового пути (4). Обе опоры имеют жесткие сочленения с мостом или одна из опор скрепляется с мостом при помощи шарниров.
Рис. 1 Контейнерный козловой кран.
Двухбалочных мосты козловых кранов состоят из одной или двух главных (и иногда двух торцевых) балок (5). По мосту, по рельсовому подтележечному пути, также ограниченному тупиковыми упорами подтележечного пути, перемещается грузовая тележка (6). На грузовой тележке могут быть установлены механизмы подъема и передвижения тележки. К тележке (к механизму подъема) посредством канатов (7) подвешивается грузозахватное устройство (8). Также к тележке крепится кабина крановщика (9). Опорные стойки устанавливаются на ходовые тележки (10) посредством балансиров. На них же устанавливаются механизмы передвижения крана (11).
Для доступа крановщика и обслуживающего персонала или другие места предусматриваются галереи, лестницы, площадки.
Также введем еще один элемент – устойчивость крана – нахождение крана в нормальном вертикальном рабочем положении.
*Примечание: Курсивом выделены элементы крана, состояние которых учитывается при составлении дерева исходов.
Понятия о случайных событиях и о вероятности возникновения события
При научном исследовании различных физических и технических задач часто приходится встречаться с особого типа явлениями, которые принято называть случайными. Случайное явление — это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному. Совершенно очевидно, что в природе нет ни одного физического явления, в котором не присутствовали бы в той или иной мере элементы случайности. В некоторых случаях отличиями, если они незначительны, можно пренебречь, рассматривая вместо реального явления его упрощенную схему, «модель», и предполагая, что в данных условиях опыта явление протекает вполне определенным (детерминированным) образом. При этом из бесчисленного множества факторов (условий), влияющих на данное явление, выделяются самые главные, основные, решающие; влиянием остальных, второстепенных факторов просто пренебрегают. Т.е., реализуется строгая причинно-следственная связь. Когда ее нет, и необходимо учесть влияние большого числа различных факторов, учитывая их взаимное влияние, что практически не реально, используют методы теории вероятностей.
|
|
|
Теория вероятностей оперирует следующими понятиями.
Под «событием» в теории вероятностей понимается всякий факт, который в результате опыта может произойти или не произойти. Обозначаются события прописными буквами латинского алфавита «А», «B», «C» и т.д.
Рассматривая различные события, мы видим, что каждое из них обладает какой-то степенью возможности: одни — большей, другие — меньшей. Вероятность события есть численная мера объективной возможности события. Обозначается обычно 
, 
, 
и т.д.
Событие А, которое в результате опыта непременно должно произойти, называется достоверным. Событие (
), которое в данном опыте не может произойти, называется невозможным. Вероятность достоверного события равна 
, невозможного – 
.
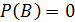Несколько событий в данном опыте (А, B, C) образуют полную группу событий, если в результате опыта непременно должно появиться хотя бы одно из них. Это можно записать следующим образом 
.
Несколько событий называются несовместными в данном опыте, если никакие два из них не могут появиться вместе.
Два события называются противоположными (А и 
), если в данном опыте они несовместны и одно из них обязательно происходит.
|
|
|
Несколько событий в данном опыте называются равновозможными, если по условиям симметрии есть основание считать, что ни одно из этих событий не является объективно более возможным, чем другое.
События, образующие полную группу, несовместные и равновозможные, называются случаями или элементарными событиями.
Случай называется благоприятным некоторому событию, если появление этого случая влечет за собой появление данного события.
Вероятность события А вычисляется как отношение числа благоприятных случаев 
к общему числу случаев 
:
Два события называются зависимыми, если вероятность появления каждого из них зависит от того, появилось другое событие или нет.
Два события называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет.
Событие А называется благоприятствующим событию B, если наступление события А влечет за собой наступление события B.
Суммой событий А и В называется событие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В.
Произведением событий А и В называется событие С = AB, состоящее в том, что в результате испытания произошли и событие А, и событие В.
Условной вероятностью Р (А/В) события В называется вероятность события В, найденная в предположении, что событие А уже наступило.
|
|
|
