 |
Частотные расширения и сжатия
|
|
|
|
Итак, возвращаясь к основному положению, у нас имеется восемь основных положений или фаз, в которых могут располагаться тетраэдр и октаэдр.
Однако любой проницательный читатель уже заметил, что восьми основных геометрических положений явно недостаточно для формирования всей Периодической Таблицы; чтобы создать полный набор природных элементов, должны работать еще какие-то дополнительный свойства.

Рис. 4.5 Частотное расширение тетраэдра в октаэдр
Вот ключ:
Обе геометрические формы способны расширяться и сжиматься из центров.
Это называется изменением частоты.
Меняя частоту, они формируют разные виды геометрических твердых тел.
Эти твердые тела не обязательно Платоновы, могут быть и другие формы, такие как твердые тела Архимеда, но все они связаны посредством “родительских” тетраэдра и октаэдра.
Как видно на рис. 4.5, сжатие геометрической формы – это деление всех ребер на две или более равных частей, а затем соединение полученных точек.
Если мы делим каждое ребро на половины, это называется “второчастотное” деление, если мы делим каждое ребро на три равные части, такое деление называется “третьечастотное” деление. Начиная с тетраэдра, Бакминстер Фуллер продемонстрировал, что посредством процесса расширения или сжатия можно получить всего десять разных частот (геометрических форм), и это центральный аспект открытий Джонсона.
Например, известно, что “мощная” сила в атомном ядре в десять раз сильнее “слабой” силы в электронных облаках! (Обычно это записывается как √100 = 10.)
Никакого иного правдоподобного объяснения этой аномалии не найдено. То есть, ядро представляет собой точку самой “свернутой” геометрии на самом высоком частотном уровне сжатия.
|
|
|
Итак, все, что нужно сделать, - это объединить восемь основных фаз вращающейся в противоположных направлениях геометрии с разными частотами геометрии, возникающей в результате расширения или сжатия.
Таким способом можно получить всю Периодическую Таблицу. Кроме того, вы можете предсказать, будет ли элемент твердым телом, жидкостью или газом и каковы будут его точки замерзания, плавления или испарения. Джонсон направляет заинтересованных мыслителей к работе Джеймса Картера, которому удалось получить всю Периодическую Таблицу посредством схем спиралевидного движения, которые он назвал “круглонами”. И самое интересное: “круглоны” Картера являются сферическими торами!
Представляется, что Картер не знал, что спиралевидные, волнообразные, циклические “вращения во вращениях” и были тем, что он изображал между круглонами для демонстрации различных элементов, то есть, они существуют посредством “абсолютного движения”.
В поисках более полного описания мы приглашаем читателя, ознакомиться с нашей детальной статьей и/или вебсайтом Картера. В целях упрощения мы приведем некоторые наиболее очевидные признаки из квантовой физики, указывающие на работу Платоновых геометрий.
ПОСТОЯННАЯ ПЛАНКА И “КВАНТОВАННАЯ” ПРИРОДА СВЕТА
Большинство людей уже знает, что тепловое излучение и свет создаются очень простой вещью – движением вспышек электромагнитной энергии, известных как “фотоны”.
Однако до 1900 года считалось, что свет и тепло движутся не в форме дискретных (прерывистых) единиц “фотонов”, а гладко, плавно и неразрывно. Физик Макс Планк первым открыл, что на самом крошечном уровне свет и тепло движутся “пульсациями” или “пакетами” энергии, величиной 10-32 см. (По сравнению с таким размером атомное ядро было бы величиной с планету!)
|
|
|
Интересно, что чем быстрее колебание, тем больше пакеты, и, соответственно, чем медленнее колебание, тем меньше пакеты.
Планк открыл, что отношение между скоростью колебания и размером пакета всегда остается постоянным, независимо от того, как вы их измеряете. Постоянное отношение между скоростью колебания и размером пакета известно как Закон Распределения Вейна.
Планк обнаружил единственное число, выражающее это отношение. Сейчас оно известно как “Постоянная Планка”.
Недавно опубликованная статья Каролин Хартман (декабрьский 2001 года выпуск журнала Наука и техника 21-го века) посвящена исключительно открытиям Макса Планка. Она раскрывает, что головоломка, созданная его открытиями, остается нерешенной:
“Сегодня, в целях более глубокого проникновения в структуру атома, наш долг – продолжать исследования таких ученых как Кюри, Лиза Мейтнер и Отто Ган.
Но фундаментальные вопросы: Что вызывает движение электронов, подчиняется ли оно определенным геометрическим законам, и почему одни элементы устойчивее, чем другие, еще не имеют ответов и ожидают новых передовых гипотез и идей”.
В этой книге мы уже можем видеть ответ на вопрос Хартман. Как мы уже сказали, открытия Планка совершались в результате изучения теплового излучения. Вводный параграф в статье Каролин Хартман – это совершенное описание его достижений:
“Сто лет назад 14 декабря 1900 года физик Макс Планк (1858-1947) объявил (в речи перед Обществом Кайзера Вильгельма в Берлине) об открытии новой формулы излучения, которая могла бы описывать все закономерности, наблюдаемые при нагревании материи, когда она начинает испускать тепло разных цветов.
Причем новая формула основывалась на одном важном допущении - энергия излучения непостоянна, излучение происходит лишь пакетами определенного размера.
Трудность в том, как сделать стоящее за “формулой” допущение физически понятным. Что имеется в виду под “энергетическими пакетами”, которые даже непостоянны, а меняются пропорционально частоте колебания (Закон Распределения Вейна)?”
Немного позже Хартман продолжает:
“(Планк) знал, когда бы вы ни наталкивались на, по-видимому, неразрешимую проблему в Природе, в ее основе должны лежать более сложные закономерности; другими словами, должна быть иная “геометрия Вселенной”, чем считалось раньше.
|
|
|
Например, Планк всегда настаивал на том, что надежность уравнений Максвелла следует пересмотреть, потому что физика достигла такой стадии развития, на которой так называемые “физические законы” больше не универсальны”.
Зерно работы Планка можно выразить простым уравнением, описывающим, как излучающая материя высвобождает энергию в “пакетах” или вспышках.
Это уравнение Е = hv, где Е – это конечная измеряемая энергия, v – частота вибрации излучения, высвобождающего энергию, и h – известна как “Константа Планка”, регулирующая “поток” между v и E.
Константа Планка равна 6,626. Это отвлеченное выражение, поскольку выражает чистое отношение между двумя величинами и не нуждается в присвоении любой определенной категории измерения, иной, чем эта.
Планк открыл эту константу не чудом, скорее он скрупулезно вывел ее посредством изучения многих разных видов теплового излучения.
Это первая главная тайна, которую проясняет Джонсон в своем исследовании. Он напоминает, что для измерения константы Планка используется (прямоугольная) система координат Декарта.
Эта система названа по имени ее создателя Рене Декарта и означает, что для измерения трехмерного пространства используются кубы.
Она стала настолько привычной, что большинство ученых даже не считают ее чем-то необычным - просто длина, ширина и высота.
В экспериментах, таких как эксперименты Планка, для измерения энергии, движущейся через определенную область пространства, используется маленький куб. В системе измерений Планка в целях простоты этому кубу был естественно присвоен объем “единицы” (1).
Однако когда Планк писал свою константу, он не хотел иметь дело с десятичным числом, поэтому он сдвинул объем куба до 10. Это сделало константу равной 6,626 вместо 0,6626.
По-настоящему важным было отношение между чем-то, находящимся внутри куба (6,626), и самим кубом (10).
Не имеет значения, присваиваете ли вы кубу объем единицы, десяти или любого другого числа, поскольку отношение всегда остается постоянным. Как мы говорили, Планк разгадал постоянную природу этого отношения лишь посредством скрупулезных многолетних экспериментов.
|
|
|
Помните, что в зависимости от размера высвобождаемого пакета вам понадобиться измерять его кубом разного размера.
И все же, что бы ни находилось внутри куба, оно всегда будет иметь 6,626 единиц объема куба, если объем самого куба 10 единиц, независимо от вовлеченных в процесс размеров.
Прямо сейчас следует отметить - величина 6,626 очень близка к 6,666, что составляет ровно 2/3 от 10. Поэтому следовало бы спросить: “Почему так важны 2/3?”
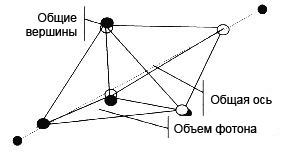
Рис. 4.6 Два тетраэдра, соединенные общей гранью
для формирования “фотона”, измеренного с помощью Постоянной Планка
Основываясь на простых измеряемых геометрических принципах, объясненных Фуллером и другими, мы знаем, что если тетраэдр совершенно разместить внутри сферы, он будет заполнять ровно 1/3 общего объема сферы. То есть 3,333 от 10.
На самом деле фотон состоит из двух соединенных вместе тетраэдров, что мы видим на рис. 4.6. Затем они вместе проходят через куб, который достаточно велик лишь для того, чтобы вмещать один из октаэдров за раз.
Общий объем (энергии), движущейся через куб, будет ровно 2/3 (6,666) общего объема куба, которому Планк присвоил число 10.
Бакминстер Фуллер первым открыл, что фотон составлен двумя тетраэдрами. Он объявил об этом миру в 1969 году на Planet Planning, после чего это было полностью забыто.
Небольшая разница 0,040 между “чистым” 6,666 или отношением 2/3 и константой Планка 6,626 создается удельной емкостью вакуума, который поглощает некоторое количество энергии.
“Удельную емкость вакуума” можно точно вычислить с помощью того, что известно как уравнение Кулона.
Выражаясь более простыми терминами, энергия эфира “физического вакуума” будет поглощать небольшое количество любой проходящей через него энергии.
Это значит, что физический вакуум будет “позволять” проходить через себя чуть меньше энергии, чем высвобождено изначально.
Поэтому, как только мы учитываем уравнение Кулона, числа работают совершенно. Более того, если мы измеряем пространство, пользуясь тетраэдральными координатами вместо кубических, необходимость в уравнении Планка Е = hv отпадает. В этом случае энергия будет измеряться одинаково на обеих сторонах уравнения, то есть Е (энергия) будет равна v (частоте), и “константа” между ними не нужна.
“Пульсации” энергии, продемонстрированные константой Планка, известны квантовым физикам как “фотоны”. Обычно мы думаем о “фотонах” как о носителях света, но это лишь одна из их функций.
|
|
|
Важнее, что когда атомы поглощают или высвобождают энергию, она передается в форме “фотонов”.
Исследователи, такие как д-р Мило Вольф, напоминают: единственное, что мы точно знаем о термине “фотон”, - он является импульсом, проходящим через эфир/энергетическое поле нулевой точки.
Сейчас можно видеть, что эта информация содержит геометрический компонент, что дает основание полагать, что и атомы должны обладать той же геометрией.
ТЕОРЕМА БЕЛЛА
Еще одной недавно открытой аномалией, демонстрирующей присутствие геометрии на квантовом уровне, является Теорема Неравномерности Белла.
В данном случае два фотона высвобождаются в противоположных направлениях. Каждый фотон испускается из отдельной возбужденной атомной структуры. Обе атомные структуры состоят из идентичных атомов, и обе распадаются с одинаковой скоростью.
Это позволяет двум “спаренным” фотонам с одинаковыми энергетическими качествами одновременно высвобождаться в противоположных направлениях. Затем оба фотона проходят через поляризационные фильтры, такие как зеркала, что теоретически должно изменить направление движения.
Если одно зеркало расположено под углом 45º, а другое под углом 30º, было бы естественно ожидать, что угловые повороты фотонов будут разными.
Однако когда выполнялся этот эксперимент, несмотря на разницу в углах зеркал, фотоны одновременно совершили одинаковый угловой поворот!
Степень точности эксперимента ошеломляет, что описывается на страницах 142-143 книги д-ра Мило Вольфа:
“В самом последнем эксперименте Аспекта для полного устранения любой возможности местных влияний одного детектора на другой Дэлибард и Роджер пользовались акустико-оптическими переключателями на частоте 50 Мг, сдвигающими наборы поляризаторов во время полета фотонов…
Теорема Белла и результаты эксперимента свидетельствуют о том, что части Вселенной связаны между собой на каком-то внутреннем уровне (то есть, не очевидном для нас), и эти связи фундаментальны (квантовая теория фундаментальна).
Как мы можем их понять? И хотя проблема анализировалась очень глубоко (Вилер и Зурек, 1983; д’Эспанья, 1983; Герберт, 1985; Стап, 1982; Бом и Хили, 1984; Пэйджелс, 1982; и другие), решение не найдено.
Авторы склонны согласиться со следующим описанием нелокальных связей:
1. Они связывают события в отдельных местах без известных полей или материи.
2. Они не ослабляются с расстоянием; будь то миллион километров или сантиметр.
3. Представляется, что они распространяются быстрее, чем скорость света”.
Бесспорно, в рамках науки это весьма озадачивающий феномен.
Теорема Белла гласит: энергетически спаренные “фотоны” реально удерживаются вместе единственной геометрической силой, а именно тетраэдром, продолжающим расширяться (становиться больше) при разделении фотонов.
Так как геометрия между ними расширяется, фотоны будут продолжать сохранять одинаковое угловое фазовое положение относительно друг друга.
ЭЛЕКТРОМАГНИТНАЯ ВОЛНА
Поскольку Эйнштейн определил, что материя состоит из электромагнитной энергии, следующий пункт нашего исследования – сама электромагнитная волна.
Как знает большинство людей, электромагнитная волна имеет два компонента – электростатическую волну и магнитную волну, которые движутся вместе. Интересно, что две волны всегда перпендикулярны друг другу.
Для визуализации происходящего Джонсон просит взять два карандаша одинаковой длины и установить их перпендикулярно друг другу; причем расстояние между ними должно равняться длине карандаша:

Рис. 4.7 Два карандаша, расположенные
на одинаковом расстоянии под углом 90º
Теперь мы можем соединить каждый конец верхнего карандаша с каждым концом нижнего карандаша. Сделав это, мы получим четырехсторонний объект, составленный равносторонними треугольниками между двумя карандашами, то есть тетраэдр.
Тот же процесс можно проделать с электромагнитной волной, приняв общую высоту электростатической или магнитной волны (которые обладают одинаковой высотой или амплитудой) за основную длину, как у карандашей на рис. 4.7.
На рис. 4.8 можно видеть, что если мы соединим линии, пользуясь тем же процессом, электромагнитная волна на самом деле копирует “скрытый” (потенциальный) тетраэдр:

Рис. 4.8 Скрытые отношения тетраэдра в электромагнитной волне
Здесь важно упомянуть, что этот секрет неоднократно открывался разными мыслителями лишь для того, чтобы снова оказаться забытым наукой.
Работа Тома Бирдена убедительно показала, что Джеймс Клерк Максвелл знал об этом, когда писал свои сложные “кватернионные” уравнения. Позднее Оливер Хэвисайд разбил модель на четыре простых кватерниона и разрушил скрытый внутренний “потенциал” тетраэдра.
Скрытый тетраэдр наблюдается и у Уолтера Расселла, а позже у Бакминстера Фуллера. Совершая свои открытия, Джонсон не знал о предыдущих прорывах.
|
|
|


