Область применения МАИ, его суть.

Понятие модели, моделирования, изоморфизм, гомоморфизм, цель, подобие и его виды.

Модель –это материальный или мысленно-представляемый объект, который с заданной степенью точности воспроизводит оригинал.

Моделирование- это воспроизведение исследуемого объекта на другом объекте – модели, изучение которого дает новую информацию об объекте оригинале.

В теории моделирования используются понятия гомоморфизм (предполагает неполное соответствие между объектом и моделью) и изоморфизм (объекты имеют тождественную структуру).

В основе моделирования лежит теория подобия, которая утверждает, что абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же, в соответствии с этим принципом различают следующие виды подобия между объектом оригиналом моделью:

1)При физическом подобии объект и модель имеют одинаковую или сходную физическую форму

2)При структурном подобии отмечают сходства между структурой объекта и модели

3)При функциональном подобии имеется сходство выполняемых объектом и моделью функциями

4)При динамическом подобии имеется сходство между вероятностными процессами в объекте и модели.

 

 

Область применения метода экспертных оценок, его суть.

В сложных производственно-экономических системах для количественной или порядковой оценки явлений и процессов, которые непосредственно измерить нельзя используется метод экспертных оценок.

Этапы процедуры экспертных исследований:

1)Формирование списка факторов исследователем

2)Подготовка анкеты

3)Формирование группы экспертов

4)Постановка задачи экспертам

5)Проведение опросов экспертов

6)Составление сводной таблицы результатов опросов

7)Обработка и оценка результатов опроса

Понятие имитационного моделирования. Система массового обслуживания.

Метод имитационного моделирования- это численный метод экспериментирования на ЭВМ с моделями, описывающими поведение сложной производственно-экономической системы в течение заданного периода времени.

Цель имитационного моделирования- воспроизведение поведения системы на основе анализа наиболее существенных взаимосвязей между ее элементами и описанием их с помощью логико-математических соотношений.

Системами массового обслуживания называются математические модели систем, которые предназначены для обслуживания требований (заявок), поступающих через случайные промежутки времени, причем длительность обслуживания в общем случае также случайна.

Классификационные признаки и виды моделирования производственных систем.

1.В зависимости от целей и предмета моделирования различают теоретические и прикладные модели. Теоретические модели отображают общие свойства экономики и ее компонентов с помощью метода дедукции, позволяющего делать выводы из формальных предпосылок. Прикладные модели обеспечивают возможность оценки параметров функционирования конкретных технико-экономи-ческих объектов и обоснования выводов для принятия управленческих решений.

2.По форме представления объектов и в зависимости от используемых средств моделирования все модели делятся на материальные и идеальные (абстрактные). Материальные модели воспроизводят основные геометрические, физические, динамические и функциональные характеристики изучаемого объекта. К материальным моделям относятся физические и аналоговые модели.От предметного моделирования принципиально отличается абстрактное (идеальное) моделирование, которое основано не на материальной аналогии объекта и модели, а на аналогии идеальной, мыслимой.Различают следующие типы идеального моделирования: интуитивное (мысленное) и знаковое (семиотическое).

3.По масштабу моделируемой системы различают модели производственно-экономических систем, модели региональных комплексов, отраслевые модели, модели народного хозяйства.

4.В соответствии с общей классификацией предмета моделирования модели подразделяются на функциональные и структурные, а также включают структурно-функциональные формы.

5.Так же модели делятся на макро и микроэкономические модели. Макроэкономические модели обычно описывают экономику страны как единое целое, связывая между собой укрупненные материальные и финансовые показатели. Модели, отображающие отдельные звенья или процессы экономики, называются микроэкономическими.

6. По периодам планирования различают модели перспективного (или стратегического) планирования, текущего и оперативно-календарного планирования.

7. По характеру используемых математических соотношений модели подразделяются на линейные и нелинейные. В линейных моделях все ограничения и функция цели описываются линейными соотношениями. В нелинейных – все или часть ограничений или функция цели – это нелинейные соотношения.

8.По степени достоверности и характеру отражения причинно-следственных связей модели делятся на детерминированные и стохастические. Детерминированные – это модели, в которых все ограничения и функция цели описываются с помощью детерминированных. Стохастические (вероятностные) – это модели, в которых учитывается случайный характер протекающих экономических процессов.

9. В зависимости от постоянства или изменчивости процессов и способам отражения фактора времени различают статические и динамические модели.

Область применения МАИ, его суть.

При внутрифирменном планировании часто воздействие той или иной стратегии не может быть выражена количественно или же количественная оценка такого влияния представляется в виде широкого диапазона значений показателей.

Кроме того имеется ряд факторов, оцениваемых не абсолютными, а ранговыми показателями.

В данных условиях актуальным становится метод анализа иерархий (МАИ). В МАИ используется шкала попарного сравнения альтернатив:

1-один сценарий одинаково вероятен, важен, значим по сравнению с другими

3 (1/3)-несколько вероятнее (невероятнее), важнее (не важнее), лучше (хуже)

5(1/5)-ощутимо вероятнее (невероятнее), важнее (не важнее), лучше (хуже)

7(1/7)-намного вероятнее (невероятнее), важнее (не важнее), лучше (хуже)

9(1/9)-крайне вероятнее (невероятнее), важнее (не важнее), лучше (хуже)

Планирование имитационных экспериментов. Функция отклика и оптимизации по градиенту, полный и неполный ф-ый экспиремент.

Основная задача планирования имитационного эксперимента (ИЭ) заключается в контроле достоверности (точности) результатов моделирования. В практике имитационного моделирования систем сложились два основных способа осуществления имитационного эксперимента (ИЭ), называемые соответственно параллельным экспериментом и последовательным экспериментом.Параллельный ИЭ - это «классический» эксперимент, в котором процесс воспроизводится многократно, и каждая реализация процесса (реплика) является статистически независимой от других реплик. Последовательный ИЭ применяется в случае моделирования эргодических процессов и основан на том, что среднее значение эргодического процесса, найденное «по времени», равно среднему, найденному «по множеству.

В планировании экспериментов для описания результирующей характеристики (в нашем случае - критерия оптимальности) используют полиномиальные модели, аппроксимирующие реальный вид целевой функции:

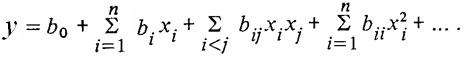
Эта функция в планировании экспериментов называется функцией отклика или уравнением регрессии, пространство, в котором строится функция отклика, - факторным пространством (рис. 34). Коэффициенты функции отклика b ₀, b_i, b_ij, b_ii и т.п. можно интерпретировать как значения частных производных в точке, вокруг которой производится разложение в ряд неизвестной целевой функции. Для поиска оптимума в области определения факторов выбирают произвольную точку А₁. В окрестности точки А₁ выделяют малую подобласть, в которой возможно описать функцию отклика полиномом первой степени (рис. 35). В этой подобласти осуществляют небольшую серию экспериментов (точки I), необходимую для построения линейной модели:

Коэффициенты регрессии b_i используются для определения направления градиента, следуя которому осуществляют дальнейшие опыты (точки II в окрестности точки А₂). Для каждой новой подобласти вновь определяют направление градиента, по которому следуют в дальнейших опытах до тех пор, пока не достигнут оптимума - области М.

Основной принцип одного из видов активного эксперимента, который называетсяполным факторным экспериментом (ПФЭ), заключается в том, что каждый уровень какого-либо фактора в эксперименте исследователь варьирует вместе со всеми уровнями остальных факторов. Этот метод статистического планирования основан на регрессионном анализе. Для того чтобы исследовать k факторов на m уровнях, требуется выполнить т опытов. Обычно простейшие методы планирования предполагают изменение каждого из факторов на двух уровнях. Для определения коэффициентов линейного уравнения при числе переменных больше 2 применяют не полный факторный эксперимент, а его части — дробные реплики.

7.Этапы моделирования производственных систем:

1 этап: разработка концепции модели – на этом этапе при постановке задачи необходимо определить главное в анализируемой системе, выделить ее характерные черты. Качественный анализ экономической проблемы позволит правильно сформировать цель исследования, т.к. от этого зависит качество полученных результатов. При определении параметров и переменных составляется перечень входных, выходных и управляемых переменных, а так же внешних и внутренних параметров системы. Разработка концептуальной модели завершается составлением содержательного описания, которое используется как основной документ характеризующий результаты работы на этом этапе.

2 этап: построение (выбор) модели –на этом этапе выбирается или строится модель наиболее подходящая для описания исследовательской проблемы – это этап формализации экономической ситуации, выражающий ее в виде конкретной математической зависимости и отношениях. Обычно сначала определяется основная конструкция математической модели, и изучаются возможности ее применения, а затем уточняются детали этой конструкции. Переменными в модели являются экономические величины, которые могут принимать любое значение из некоторого множества допустимых величин. Различают экзогенные переменные (принимаются независимыми) и эндогенные (получают свое значение в результате решения задачи на модели при заданных значениях экзогенных переменных).

3 этап: эксперимент на модели – этот этап включает численное решение поставленной задачи с помощью модели и получение новых знаний об объекте оригинале. Численное решение предполагает разработку алгоритмов для решения задачи, составление программ для ЭВМ и непосредственное проведение расчетов. Прежде всего выбирается язык программирования, затем составляется план проведения эксперимента, результаты моделирования могут быть представлены в виде таблиц, графиков и т.д.

4 этап: применение полученных знаний – на этом этапе решается вопрос о правильности и полноте результатов моделирования и о степени их практической применимости.

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: