Информац. подход. Понятие и расчёт энтропии, её св-ва.

Непременным условием функционирования любой сложной производственно-экономической системы является получение, обработка, передача и хранение технической, технологической, социальной, экономической и других видов информации. В этом процессе всегда происходит обмен информацией между различными звеньями системы и с окружающей средой с помощью линий прямой и обратной связи.

Любое сообщение, с которым мы имеем дело в сложных производственно-экономических системах, представляет собой совокупность сведений о параметрах данной системы. Сообщение приобретает смысл в том случае, если состояние системы заранее неизвестно, случайно, неопределенно в какой-то степени. Неопределенность в производственно-экономической системе – это ситуация, когда полностью или частично отсутствует информация о возможных состояниях системы и внешней среды, т.е. когда в системе возможны те или иные непредсказуемые события (вероятностные характеристики которых неизвестны).

Различают: 1) истинную неопределенность вследствие многовариантности развития или невозможности однозначного выбора эффективных вариантов решений и 2) информационную неопределенности, возникающую из-за неполноты и неточности информации об исследуемых процессах. Также различают: а) неопределенность “природы”, т.е. внешней среды по отношению к рассматриваемой системе; б) неопределенность целей; в) неопределенность действий противника в случае конфликтных ситуаций, конкуренции и т.п.

В качестве меры априорной неопределенности системы применяется специальная характеристика – “энтропия”. Энтропия системы определяется как сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком (формула Шеннона):

Свойства энтропии: 1) она обращается в нуль, когда одно из состояний системы достоверно, а другие – невозможны;

2) при заданном числе состояний она обращается в максимум, когда эти состояния равновероятны, а при увеличении числа состояний – увеличивается

при р1 = р2 =…= рi =…= pn =1/n;

т.е. Нmax(S) = log2 n – (формула Хартли);

3) она обладает свойством аддитивности, т.е. когда несколько независимых систем объединяются в одну, их энтропии складываются

Н(S, K) = H(S) + H(K).

17.Модель оптимально планирования производства. Графический метод отыскания экстремума в линейных моделях математического програмирования.

Критерий оптимальности – некоторый показатель, имеющий экономическое содержание, который является формализацией цели управления и выражается в виде целевой функции через факторы модели

Критерий оптимальности – это смысловое содержание целевой функции.

Система ограничений определяет пределы, которые ограничивают область допустимых решений и фиксируют основные внешние и внутренние свойства объекта. Ограничения определяют область протекания процесса, пределы изменения параметров и характеристик объекта.

Математическая формализация системы ограничений – уравнение связи представляется в виде системы уравнений и неравенств:

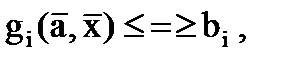
где - целевая функция; x_j – управляемые переменные, ; g_i – формализованное представление системы ограничений, ; b_i – некоторые действительные числа (ограничения по плану, ресурсам и др.).

Решение экономико-математической модели – это совокупность значений переменных, которая удовлетворяет системе ограничений (уравнениям связи). Оптимальным решением является такое, при котором функция цели достигает своего экстремального значения (min или max)

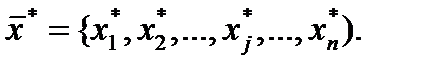
Геометрический подход к решению задач линейного программирования

Геометрический метод решения задач ЛП имеет весьма ограниченное применение и главным образом используется для наглядной иллюстрации существа подобных задач.

В этой связи отметим, что если система ограничений задачи ЛИ задана в виде системы линейных неравенств с двумя переменными или в виде системы линейных уравнений, В которой число переменных на две больше, чем число уравнений, то такая задача может быть решена геометрически.

Если размерность задачи линейного программирования позволяет представить область определения переменных в виде многоугольника, расположенного в первом квадранте системы координат, то экстремум целевой функции находится в одной из его вершин, а ее координаты соответствуют оптимальному решению.