 |
Выбор необходимых параметров rc -цепочки, согласно критериям технического задания
|
|
|
|
При анализе формул (1) и (2) можно заметить, что сопротивление резистора r и ёмкость конденсатора С входят в формулы АЧХ и ФЧХ только в виде произведения τ=r∙C. Это произведение является постоянной времени для rc-цепочки. Известно, что приемлемая точность дифференцирования обеспечивается в том случае, когда постоянная времени цепи хотя бы на два порядка меньше наименьшего интервала времени, в пределах которого функция u1(t) изменяется с наибольшей скоростью. В данном случае достаточно, чтобы τ была в сто раз меньше половины периода высшей(второй) гармоники полезного сигнала, т.е. τ = r∙C =  . Период высшей гармоники полезного сигнала определяется, как
. Период высшей гармоники полезного сигнала определяется, как 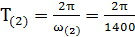 . Тогда
. Тогда
τ = r∙C =  ≈ 22,4∙
≈ 22,4∙ 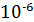 (с).
(с).
Выберем ёмкость С = 1мкФ, тогда сопротивление r = 22,4 (Ом).
С учётом выбранных r и С окончательно получаем τ = 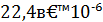 (с). Для этой постоянной времени построим амплитудно-частотную и фазо-частотную характеристики.
(с). Для этой постоянной времени построим амплитудно-частотную и фазо-частотную характеристики.
По формуле (1):  .
.
По формуле (2):  .
.

| 
|
ФЧХ rc-цепочки с выбранными параметрами r и c ФЧХ идеального дифференцирующего устройств
Входной сигнал имеет вид:
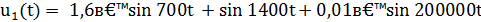
Найдем значения АЧХ и ФЧХ для частот сигнала:
 =700 рад/с
=700 рад/с 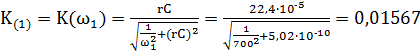
 =700 рад/с
=700 рад/с 
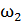 =1400 рад/с
=1400 рад/с 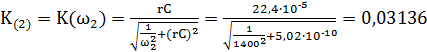
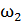 =1400 рад/с
=1400 рад/с 
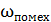 =200000 рад/с
=200000 рад/с 
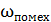 =200000 рад/с
=200000 рад/с 
Выходной сигнал:
Общая формула для вычисления: 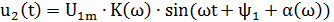
Выходной сигнал без помехи:
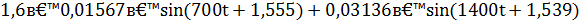
Выходной сигнал с помехой:
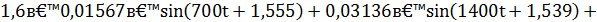
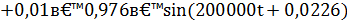
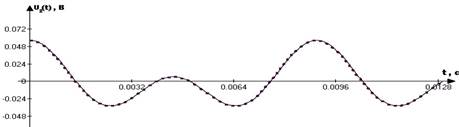
Рис.8 – Выходной сигнал
Выхондой сигнал без помехи найденный с помощью АЧХ и ФЧХ rc-цепочки на полезных частотах сигнала. Формула для нахождения каждой из составляющих выходного сигнала: u_2 (t)=U_1m∙K(ω)∙sin(ωt+ψ_1+α(ω))
Выходной сигнал, полученный путем умножения дифференцированого входного сигнала без помехи на коэффициент m(коэффициент подбирается визуально, так чтобы графики выходных сигналов совпадали) m=0,0000224
|
|
|
u_2 (t)=0,0000224∙(1,6∙cos(700∙x)∙700+cos(1400∙x)∙1400) а

Рис.9 - Выходной сигнал с помехой
Выходной сигнал с помехой найденный с помощью АЧХ и ФЧХ rc-цепочки на полезных частотах и на частоте помехи сигнала u_2 (t)=U_1m∙K(ω)∙sin(ωt+ψ_1+α(ω))
Выходной сигнал, полученный путем умножения дифференцированого входного сигнала без помехи на коэффициент m(коэффициент подбирается визуально, так чтобы графики выходных сигналов совпадали) m=0,0000224
u_2 (t)=0,0000224∙(1,6∙cos(700∙x)∙700+cos(1400∙x)∙1400) Вывод: rc-цепочка не способна обеспечить выходной сигнал с допустимо малым уровнем помехи, необходимо искать путь подавления помехи в сигнале. Так как, при отсутствии помехи, rc-цепочка может быть использована как идеальное дифференцирующее устройство.
Теперь проанализируем полученные результаты с точки зрения критериев технического задания, всего их 3(уровень полезного сигнала, точность дифференцирования, помехоучтойчивость rc-цепочки)
Начнем проверку с третьего критерия, так как он представляется(судя по графику) невыполняемым(рис 9).
Помехоучтойчивость rc -цепочки
Для количественного определения допустимого уровня помехи в составе выходного сигнала, вычислим отношение амплитуды помехи к амплитуде первой гармоники полезного сигнала для входного сигнала u1(t):
 .
.
Приблизительно таким же (или ещё меньше) должно быть отношение амплитуд помехи и первой гармоники полезного сигнала в выходном сигнале u2(t), т.е. должно выполняться соотношение:
 (3);
(3);
Вычислим отношение амплитуд помехи и первой гармоники полезного сигнала в выходном сигнале u2(t):
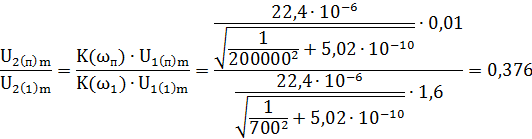
В результате соотношение (3) не выполняется, т.е. уровень помехи в составе выходного сигнала значительно превышает допустимый
|
|
|
Следовательно если один из критериев не выполняется, то нет смысла проверять и другие два.
Анализируя результат, можно сделать вывод о том, что дифференцирующая rc-цепочка с постоянной времени τ = 22,4∙ 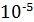 (с) обеспечивает достаточный уровень полезного сигнала на выходе и приемлемую точность дифференцирования(рис13,14). Однако, уровень помехи в составе выходного сигнала такой цепочки недопустимо высок, что не позволяет использовать её в устройстве формирования управляющих сигналов.
(с) обеспечивает достаточный уровень полезного сигнала на выходе и приемлемую точность дифференцирования(рис13,14). Однако, уровень помехи в составе выходного сигнала такой цепочки недопустимо высок, что не позволяет использовать её в устройстве формирования управляющих сигналов.
Помеху можно было бы подавить на выходе с помощью частотного фильтра. Но в этом случае необходимо учесть влияние (вполне возможно, неблагоприятное) фильтра на качество дифференцирования полезного сигнала, так как АЧХ и ФЧХ совместно работающих дифференцирующего устройства и фильтра, скорее всего, окажутся существенно хуже АЧХ и ФЧХ отдельно рассчитанной r-с цепочки.
Гораздо более удачным был бы вариант электрической цепи, которая обладала бы дифференцирующими свойствами в области частот полезных составляющих входного сигнала и одновременно свойством подавления высокочастотной помехи. Таким дополнительным свойством обладала бы цепь, в которую включена катушка индуктивности, т.е. выполненная по схеме (рис. 15):
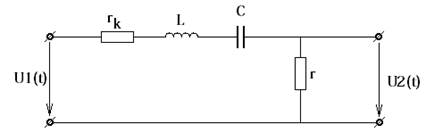
Рис. 15 Простейшая дифференцирующая r-L-c цепочка
Здесь L - индуктивность катушки, rk - ее активное сопротивление, r и c - активное сопротивление и емкость, величины которых могут остаться такими же, как и в r-с цепочке, рассмотренной ранее. Индуктивное сопротивление xL = ωL особенно велико на частоте помехи и способно существенно ограничить составляющую тока этой частоты, а следовательно, и выходное напряжение сигнала помехи, что и является ожидаемым полезным эффектом. Однако наличие дополнительных параметров L, rk изменяет вид АЧХ и ФЧХ и в области частот полезного сигнала, причем пока не ясно, в сторону их улучшения или ухудшения. Поэтому необходимо исследовать (аналитически, в общем виде) АЧХ и ФЧХ предложенной r-L-c цепи. Если имеется некоторый диапазон частот, в пределах которого АЧХ и ФЧХ одновременно отвечают условиям дифференцирования полезной составляющей входного сигнала, значит, дальнейшие операции имеют смысл. Если такого диапазона нет, цепь в принципе не обладает нужными свойствами.
|
|
|
1. Расчет в общем виде АЧХ и ФЧХ скорректированного дифференцирующего устройства (r - L - c цепи). Р асчет параметров r - L - c цепи согласно требованиям технического задания.
Составим уравнения Кирхгоффа для r-L-c-цепочки в комплексной форме (рис. 17):
 |

|

Комплексный коэффициент передачи напряжения может быть найден, как отношение комплексных амплитуд, либо как отношение действующих значений напряжений:
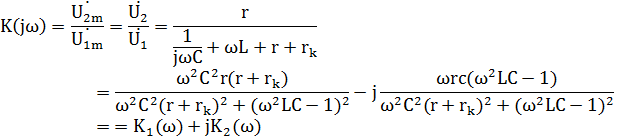
Отсюда, АЧХ:
 (4)
(4)
ФЧХ:
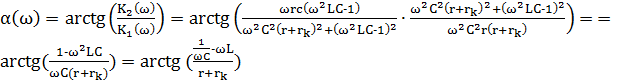 (5)
(5)
В общем виде, амплитудно-частотная и фазо-частотная характеристики дифференцирующей r-L-c-цепочки могут быть представлены в виде графиков (рис.18 и рис. 19):

| 
|
| Рис. 18 Общий вид АЧХ дифференцирующей r-L-c-цепочки, ω0 – резонансная частота | Рис. 19 Общий вид ФЧХ дифференцирующей r-L-c-цепочки, ω0 – резонансная частота |
Известно, что r-L-с цепочка является резонансной, с резонансной частотой ω0, определяемой по формуле:  .
.
Поэтому, необходимо выбрать значение резонансной частоты ω0 таким образом, чтобы обеспечить выполнение всех трёх критериев технического задания. Разумеется, значение резонансной частоты ω0 не может находиться внутри или на границе диапазона частот составляющих полезного сигнала (хотя бы потому, что значение ФЧХ при ω = ω0 равно нулю, а должно быть, в идеале, равным π/2). С другой стороны, резонансная частота не должна совпадать или быть близкой к частоте помехи (хотя бы потому, что условие ω = ω0 соответствует максимуму тока в цепи и, следовательно, максимуму напряжения на выходе, а задача состоит как раз в обратном - в необходимости максимально уменьшить это напряжение). Следовательно, положение резонансной частоты на оси частот определяется неравенством ω2< ω0< ωп, где ω2 - частота высшей гармоники полезного входного сигнала, ωп -частота помехи. Поскольку ωп намного больше ω2, диапазон возможного положения ω0 на оси частот достаточно широк, и это позволяет надеяться, что при каком-то значении индуктивности L цепь сможет соответствовать всем указанным выше критериям качества, хотя это и не гарантировано.
|
|
|
Теперь рассчитаем параметры r-L-c цепочки согласно требованиям технического задания. Как уже было отмечено ранее, параметры r и C можно оставить теми же, что были использованы при расчете rc-цепочки. Активное сопротивление катушки rk зависит от числа её витков, которое в свою очередь определяет индуктивность катушки L. Сама же индуктивность может быть вычислена, если будет известна резонансная частота ω0 r-L-c цепочки.
Проведём анализ формул для расчёта АЧХ и ФЧХ r-L-c цепочки с точки зрения критериев, описанных в техническом задании. Целью анализа будет установление интервала частот Δω, в котором может находиться резонансная частота ω0, и при этом будут выполняться все три критерия качества. При анализе можно пренебречь активным сопротивлением катушки rk, т.к. rk<<r. Поэтому можно считать, что оно не оказывает существенного влияния на характер АЧХ и ФЧХ.
C учётом сказанного, перепишем формулы (4) и (5), подставив в них зависимости:
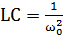 и
и 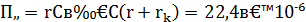 (c).
(c).
Получим:
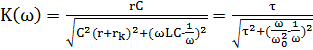 (6)
(6)
 (7)
(7)
При расчете интервала частот Δω, можно принять следующие обозначения:
ω01 - минимально-необходимое значение резонансной частоты ω0, обеспечивающее соответствие первому критерию качества,
ω02 - максимально возможное значение ω0, обеспечивающее выполнение требований второго критерия;
ω03 - максимально возможное значение ω0, обеспечивающее выполнение требований третьего критерия.
1) Расчёт резонансной частоты ω0 с точки зрения критерия минимального уровня полезного сигнала на выходе.
Составим неравенство, исходя из условия, что минимально-необходимым можно принять сигнал u2(t), у которого амплитуда первой гармоники не меньше 1мВ: 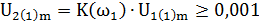 (8).
(8).
Подставив выражение для K(ω) из формулы (6), составим и решим неравенство:
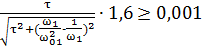 , где
, где 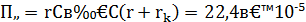 ,
,  .
.
Решая это неравенство относительно ω01, получим:
ω01– любое значение (9). Расчёт резонансной частоты ω0 с точки зрения критерия точности дифференцирования выходного сигнала.
В качестве опорных неравенств, воспользуемся неравенствами (10) и (11), которые приведены в техническом задании:
 (10) и
(10) и  (11)
(11)
Подставим из выражения (6) в неравенство (10) значения K(1)=K(ω1) и K(2)=K(ω2), получим:
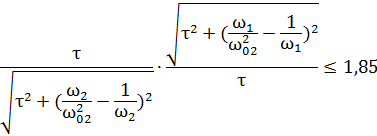
Здесь 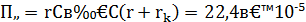 ,
,  ,
,  . Решая это неравенство относительно ω02, получим:
. Решая это неравенство относительно ω02, получим:
ω02 – любое значение (12). Подставим из формулы (7) в неравенство (11) значение  , получим:
, получим:
 .
.
Решая это неравенство относительно ω02, получим: ω02 ≥2797,5 рад/с (13)
|
|
|
2) Расчёт резонансной частоты ω0 с точки зрения критерия помехозащищённости r - L - c цепочки.
Для расчёта помехозащищённости, воспользуемся условием неравенства (6):
 (3)
(3)
Здесь 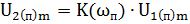 и
и 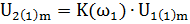 . Подставим эти значения в неравенство (3), используя формулу (6). Получим:
. Подставим эти значения в неравенство (3), используя формулу (6). Получим:
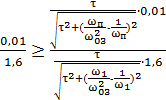 ;
;
Здесь 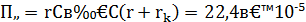 , ωп = 200000 рад/с.
, ωп = 200000 рад/с.
Решая это неравенство относительно ω03, получим:
ω03 ≤ 16741,6 рад/с (14)
Итак, наложив ограничения на резонансную частоту ω0 с точки зрения всех трёх критериев, можно составить систему из неравенств (9,12,13,14): 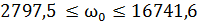 . Отсюда, искомый интервал частот Δω = (2797,5 …
. Отсюда, искомый интервал частот Δω = (2797,5 … 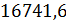 ) (рад/с). Так как в техническом задании не оговорено никаких дополнительных требований к резонансной частоте, то можно выбрать любое значение ω0 из интервала Δω. Выберем ω0 = 10000 рад/с. С учетом выбранной резонансной частоты и ранее выбранной ёмкости С = 1мкФ, вычислим индуктивность катушки L:
) (рад/с). Так как в техническом задании не оговорено никаких дополнительных требований к резонансной частоте, то можно выбрать любое значение ω0 из интервала Δω. Выберем ω0 = 10000 рад/с. С учетом выбранной резонансной частоты и ранее выбранной ёмкости С = 1мкФ, вычислим индуктивность катушки L:
 (Гн).
(Гн).
Рассчитаем число витков катушки с сердечником в виде кольцевого магнитопровода, выполненного из феррита (рис. 5) с магнитной проницаемостью μr. Пренебрегаем всеми видами потерь. Напряженность поля на одинаковом расстоянии r от оси симметрии такого магнитопровода одинакова и равна
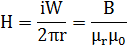
Здесь i – сила тока в катушке, W – число витков, B – магнитная индукция, μ0 = 1,25663706*10-6 Гн/м – магнитная постоянная. Магнитный поток в сердечнике равен:
 ;
;
Следовательно, индуктивность катушки без учёта индуктивности рассеяния
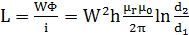 (15).
(15).
Отсюда, число витков 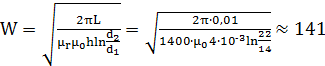
С учётом W=141, найдём индуктивность такой катушки по формуле (15):  (Гн)
(Гн)
Теперь рассчитаем активное сопротивление катушки rk::
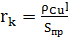 (16)
(16)
Здесь  Ом∙м – удельное сопротивление меди, l=W∙2(
Ом∙м – удельное сопротивление меди, l=W∙2( + h) – полная длинна провода в катушке,
+ h) – полная длинна провода в катушке, 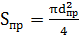 – площадь поперечного сечения проводника. Таким образом,
– площадь поперечного сечения проводника. Таким образом,
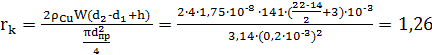 (Ом).
(Ом).
Добротность контура 
|
|
|
12 |


