 |
Задание 3. Обработка результатов нескольких серий измерений
|
|
|
|
Условие задания
При многократных измерениях одной и той же величины получены две серии по 12 (
) результатов измерений в каждой. Эти результаты после внесения поправок представлены в таблице. Вычислить результат многократных измерений.
Серия измерений 1.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 485 | 484 | 486 | 482 | 483 | 484 |
|
| 7 | 8 | 9 | 10 | 11 | 12 |
| 484 | 481 | 485 | 485 | 485 | 492 |
Серия измерений 2.
|
| 1 | 2 | 3 | 4 | 5 | 6 |
|
| 484 | 481 | 480 | 481 | 484 | 485 |
|
| 7 | 8 | 9 | 10 | 11 | 12 |
|
| 485 | 484 | 483 | 483 | 485 | 492 |
Обработка результатов производится для каждой серии отдельно.
Для обработки результатов серий измерений необходимо исключить ошибки. Число измерений лежит в диапазоне 10…15<n<40…50. Поэтому исключение ошибок проводится на основе 
критерия.
Серия измерений 1.
Определяем среднее арифметическое и среднеквадратическое отклонение результатов серии измерений 1.
Далее определяем значения 
критерия для каждого значения результата серии измерений 
по формуле:
В соответствии с доверительной вероятностью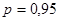 
с учетом 
находим из соответствующей таблицы значение 
, которое зависит от числа измерений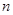 
и 
.
При 
, следовательно, значение 492 исключаем как ошибку.
Исключение ошибок продолжается до тех пор, пока не будет выполнятся условие 
.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 485 | 484 | 486 | 482 | 483 | 484 |
|
| 7 | 8 | 9 | 10 | 11 | |
|
| 484 | 481 | 485 | 485 | 485 |
Заново определяем значения критерия для каждого значения результата серии измерений по формуле:
В соответствии с доверительной вероятностью 
с учетом находим из соответствующей таблицы значение 
, которое зависит от числа измерени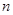й и .
Условие 
выполняется для всех результатов серии измерений.
|
|
|
Следующим шагом анализа является проверка гипотезы о нормальности распределения оставшихся результатов серии измерений. Проверка выполняется по составному критерию, так как количество результатов серии измерений лежит в диапазоне 10…15<n<40…50.
Применяя первый критерий, следует вычислить отношение:
и сравнить с 
и 
.
Задаемся рекомендуемой доверительной вероятностью 
и для уровня значимости 
определяем из соответствующей таблицы квантили распределения и .
Значение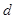 
соответствует условию 
. Первый критерий выполняется.
Применяя второй критерий, задаемся рекомендуемой доверительной вероятностью 
и для уровня значимости 
с учетом 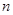по соответствующим таблицам определяем значения 
и 
.
Для из таблицы для интегральной функции нормированного нормального распределения 
определяем значение 
и рассчитываем E:
, 
.
Используя правила округления, получим:
Далее сравниваем значения 
и 
.
|
| 1 | 2 | 3 | 4 | 5 | 6 |
|
| 1 | 0 | 2 | 2 | 1 | 0 |
|
| 7 | 8 | 9 | 10 | 11 | |
|
| 0 | 3 | 1 | 1 | 1 |
Мы видим, что не более разностей 
превосходят значение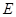 
. Следовательно, второй критерий, а вместе с тем и составной критерий выполняются полностью. Закон распределения можно признать нормальным с вероятностью
.
Серия измерений 2.
Определяем среднее арифметическое и среднеквадратическое отклонение результатов серии измерений 2.
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| 484 | 481 | 480 | 481 | 484 | 485 |
|
| 7 | 8 | 9 | 10 | 11 | 12 |
|
| 485 | 484 | 483 | 483 | 485 | 492 |
Далее определяем значения 
критерия для каждого значения результата серии измерений 
по формуле:
В соответствии с доверительной вероятностью с учетом находим из соответствующей таблицы значение 
, которое зависит от числа измерений 
и 
.
При 
, следовательно значение 492 исключаем как ошибку.
Исключение ошибок продолжается до тех пор, когда не будет выполнятся условие .
|
|
|
|
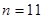
| 1 | 2 | 3 | 4 | 5 | 6 |
|
| 484 | 481 | 480 | 481 | 484 | 485 |
|
| 7 | 8 | 9 | 10 | 11 | |
|
| 485 | 484 | 483 | 483 | 485 |
Заново определяем значения 
критерия для каждого значения результата серии измерений по формуле:
В соответствии с доверительной вероятностью с учетом находим из соответствующей таблицы значение , которое зависит от числа измерений 
и .
Условие выполняется для всех результатов серии измерений.
Следующим шагом анализа является проверка гипотезы о нормальности распределения оставшихся результатов серии измерений. Проверка выполняется по составному критерию, так как количество результатов серии измерений лежит в диапазоне 10…15<n<40…50.
Применяя первый критерий, следует вычислить отношение:
и сравнить с и 
.
Задаемся рекомендуемой доверительной вероятностью 
и для уровня значимости 
определяем из соответствующей таблицы квантили распределения и .
Значение 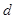соответствует условию 
. Первый критерий выполняется.
Применяя второй критерий, задаемся рекомендуемой доверительной вероятностью 
и для уровня значимости 
с учетом по соответствующим таблицам определяем значения и .
Для из таблицы для интегральной функции нормированного нормального распределения 
определяем значение и рассчитываем E:
, 
.
Используя правила округления, получим:
Далее сравниваем значения и .
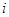
| 1 | 2 | 3 | 4 | 5 | 6 |
|
| 0,82 | 2,18 | 3,18 | 2,18 | 0,82 | 1,82 |
|
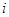
| 7 | 8 | 9 | 10 | 11 | |
|
| 1,82 | 0,82 | 0,18 | 0,18 | 1,82 |
Мы видим, что не более разностей 
превосходят значение 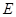. Следовательно второй критерий, а вместе с тем и составной критерий выполняется полностью. Закон распределения можно признать нормальным с вероятностью 
.
Далее необходимо проверить значимость различия средних арифметических серий.
Для этого необходимо вычислить моменты закона распределения разности:
Задавшись доверительной вероятностью 
, определяем из соответствующих таблиц интегральной функции нормированного нормального распределения 
значение 
и сравниваем 
с 
.
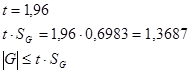
Условие 
выполняется. Различие между средними арифметическими в сериях с доверительной вероятностью можно признать незначимым.
|
|
|
Далее необходимо проверить равнорассеянность результатов измерений в сериях.
Для этого определяем значение:
И, задавшись доверительной вероятностью , определяем из соответствующих таблиц значение аргумента интегральной функции распределения вероятности Фишера 
.
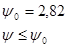
Условие 
выполняется. Серии с доверительной вероятностью 
считаем рассеянными.
Выше было показано, что серии равнорассеяны и с незначимым различием средних арифметических. Исходя из этого все результаты измерений объединяются в единый массив и затем для него выполняется обработка по алгоритму, согласно которому необходимо определить оценку результата измерения 
и среднеквадратического отклонения 
.
Задавшись доверительной вероятностью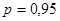 
, определяем из таблиц распределения Стьюдента значение 
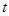для числа степеней свободы
Затем определяем доверительный интервал 
:
Используя правила округления, получим:
Результат измерений запишется в виде:
.
|
|
|
12 |
