Метод Рунге-Кутты второго порядка

 

В методах Рунге-Кутты интеграл заменяется линейной комбинацией значений подынтегральной функции, вычисленных при разных значениях аргумента:

 (7)

Метод Рунге-Кутты представим в виде:

 

                                                        (8)

 

 

Из вышеуказанных общих формул (8) получают формулы метода Рунге-Кутты 2-ого порядка m=2;

      (9)

Для определения метода необходимо найти значения вещественных коэффициентов: . Для этого интеграл, заменяемый линейной комбинацией значений подынтегральной функции, вычисленных при разных значениях аргумента, можно представить как:

       (10)

А его, в свою очередь, можно представить рядом Тейлора:

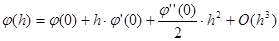 (11)

где - сумма элементов ряда Тейлора, степень которых не ниже 3.

Осталось найти неизвестные значения

  (12)

В результате таких бесхитростных манипуляций получаем искомый ряд Тейлора:

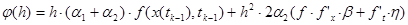       (13)

Приравняем коэффициенты при одинаковых степенях  в выражениях

(11) и (13). В итоге получим систему уравнений вида:

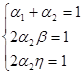    (14)

Из свойств системы (14) следует отметить, что она не обладает единственным решением. При  значение , значение , а (15)

Подставив полученные коэффициенты в соотношение (8), получаем следующие формулы метода Рунге-Кутты 2-ого порядка:

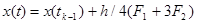
    (16)

ОПИСАНИЕ ПРОГРАММНЫХ МОДУЛЕЙ

 

Составленная в ходе курсовой работы программа вычисляет решения дифференциального уравнения, с предварительно заданными начальными условиями. Интегрирование происходит согласно двум методам: Рунге-Кутты второго и четвертого порядков.

Программа состоит из следующих модулей:

1) Основная программа;

2) Процедура вычисления точного решения ДУ;

3) Процедура вычисления правых частей;

4) Процедура выполняющая шаг интегрирования методом Рунге-Кутты 2-ого порядка;

5) Процедура выполняющая шаг интегрирования методом Рунге-Кутты 4-ого порядка.

Основная программа

 

Блок программы осуществляет следующие операции:

· запрашивает у нерадивого пользователя величину шага интегрирования и шаг вывода на экран;

· вычисляет количество шагов;

· с заданным шагом вызывает процедуры интегрирования методом Рунге-Кутты 2-ого и 4-ого порядков на отрезке интегрирования;

· вычисляет погрешность и оценку погрешности интегрирования;

· выводит замечательные результаты работы программы с заданным шагом вывода на экран.

Для простоты понимания укажем следующие переменные, содержащиеся в программе:

· h - шаг интегрирования. Вводится нерадивым пользователем с клавиатуры;

· n – число шагов интегрирования;

· h_screen - шаг вывода результатов на экран. Вводится нерадивым пользователем с клавиатуры;

· i_screen – счётчик вывода результатов на экран. Когда i_screen > h_screen, то происходит вывод результатов и обнуление i_screen;

· i, j – переменные, используемые циклом;

· e2, e4– ошибки интегрирования для методов Рунге-Кутты 2-ого и 4-ого порядков соответственно. Подсчитываются из соотношения(1):

     (1)

· e2max, e4max – оценки погрешностей интегрирования для методов Рунге-Кутты 2-ого и 4-ого порядков соответственно. Подсчитываются из соотношения(2):

                                                        (2)

 

· t – значения независимой переменной;

· t0, tf – пределы интегрирования

· y2, y4 – вектора решения для методов Рунге-Кутты 2-ого и 4-ого порядка соответственно в узле t_k;

· outfile– переменная файлового типа. Определена для вывода результатов в текстовой файл;

· name – переменная строкового типа. Используется для передачи имени файла.

Текст основной программы приведён в приложении А, схема в приложении Б.

Функция вычисления точного решения

Function clearsolve (t: real): real

Функция предназначена для вычисления точного решения для дифференциального уравнения по формуле (3):

 (3)

Текст функции приведен в приложении 2, схема в приложение 7.

123	Поделиться:

Воспользуйтесь поиском по сайту: