 |
Согласно гипотезе, суммарная погрешность алгоритма при интегрировании ДУ с постоянным шагом пропорциональна величине шага в степени, равной порядку метода.
|
|
|
|
(1)
Результаты вычислений на ПЭВМ приводятся в приложении В. Результат работы программы наглядно представлены в графическом виде (рисунок 2).
Рисунок 3 – Зависимость отношения оценки погрешности к величине шага интегрирования в степени, равной порядку метода от шага интегрирования
Гипотеза Рунге экспериментально подтверждается только при таких значениях шага (1-0.01), где погрешность вычисления ПЭВМ влияет на результат в благоразумных пределах. При дальнейшем уменьшении шага пропорциональность скрывается из виду. Это можно истолковать тем, что предположение Рунге не учитывает влияния ошибки вычисления ПЭВМ на полученный результат.
Исследование поведение ошибки интегрирования как функции независимой переменной для обоих методов Рунге-Кутты при различных значениях шага
Для проведения своих изысканий нам необходимо выбрать 3 значения шага в начале, середине и конце диапазона изменения шага и построить графические зависимости решений от независимой переменной и погрешностей интегрирования от независимой переменной.
Результаты вычислений на ЭВМ приводятся в приложении В. Результат работы программы наглядно представлены в графическом виде (рисунок 3 и 4).
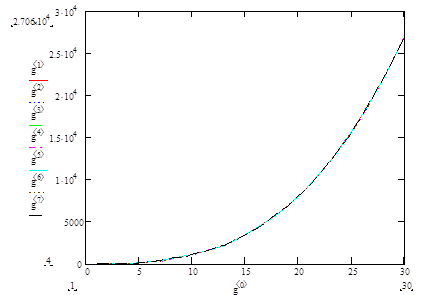
Рисунок 4 – График точного и приближенных решений (h=0.001, 0.1, 0.5) дифференциального уравнения
На рисунке 3 слегка, но все-таки заметны отклонения приближённых решений при разной величине шага от точного, что подтверждает высокую точность получаемого приближенного решения относительно точного.
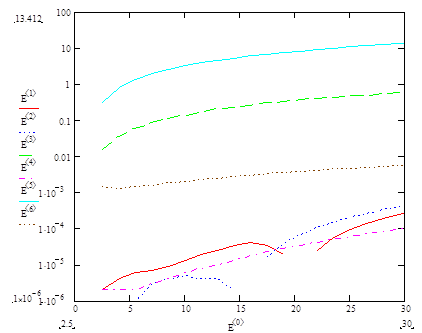
Рисунок 5 – График зависимости величины ошибки интегрирования от независимой переменной при h=0.001, 0.1, 0.5
|
|
|
При шаге, численно равном 0.5 из рисунка 5 очевидно, что различия между погрешностями методов 2-ого (E5) и 4-ого (E6) порядков довольно значительны, что объясняется более высокой точностью метода 4-ого порядка.
Разница ошибок интегрирования для обоих методов при шаге интегрирования 0.1 остается достаточно высокой, но следует подметить, что точность метода Рунге-Кутты 4-ого порядка при данном значении шага выше, чем при меньшем h=0.001 (это обусловлено тем, что алгоритмическая ошибка стремится к нулю, а вычислительная ещё не показывает свой отвратительный характер).
При величине шага интегрирования h=0.001 ошибки интегрирования (E1 и E2), равно как и при больших h возрастают с ростом независимой переменной, что слава Богу не противоречит теории, однако прослеживается скачкообразный характер графиков, что связано с внушительной лептой вычислительной ошибки в общую погрешность.
Сравнительный анализ эффективности методов Рунге-Кутты при различных требованиях к точности вычисления
Для анализа надлежит оценить затраты машинного времени на интегрирование ДУ в зависимости от величины погрешности интегрирования.
Так как для довольно непростых уравнений львиная доля времени уходит на вычисление правых частей уравнений, то в качестве оценки затрат машинного времени можно принять количество вычислений правых частей при нахождении решения на всём отрезке интегрирования, что есть произведение количества шагов интегрирования на порядок метода. Зависимость оценки ошибки интегрирования от количества шагов интегрирования определена.
Замечательные результаты вычислений на ПЭВМ приведены все в том же приложении В. Результат работы программы представлены графически (рисунок 5).
Рисунок 6 – График зависимости величины ошибки интегрирования от количества вычислений правой части
Из близлежащего графика практически определяется метод для различных требованиях к точности и времени работы нашей замечательной программы.
|
|
|
График наглядно демонстрирует, что наличествует такой предел шага, ниже которого программа гоняет свои байты зря, так как оценка погрешности растёт из-за ошибки вычисления ПЭВМ. Стало быть, на практике следует выбирать определенный промежуток шага, желательно в котором алгоритм устойчив.
ЗАКЛЮЧЕНИЕ
При реализации на практике задания для курсовой работы, заключающегося в интегрирования ОДУ, была составлена и отлажена программа, приведенная в приложении А. С помощью данной программы проведена серия опытных исследований свойств методов Рунге-Кутты второго и четвёртого порядков.
При задании определенного интервала значений шага интегрирования ошибка интегрирования уменьшается с уменьшением шага. Подтверждение сего факта можно без труда найти в теории. Однако нельзя обойти вниманием тот труднооспоримый аргумент, что для довольно незначительных значений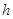 
с уменьшением шага интегрирования ошибке свойственно увеличивается. Это связано с лавинообразным ростом числа требуемых для получения решения вычислений и c увеличением ошибки вычислений.
На заданном интервале значений 
(при условии, что на интервале ошибка вычислений велика не до безобразия), при одинаковых значениях шага интегрирования метод Рунге-Кутты четвёртого порядка имеет достаточно малую ошибку вычисления относительно ошибки метода Рунге-Кутты второго порядка.
Следует отметить, что коэффициент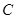 
(формула (1) раздела 3) для таких значений шага интегрирования, при которых можно скрипя сердцем считать его неизменным, имеет меньшее значение для метода Рунге-Кутты четвёртого, нежели второго порядка. Отсюда мораль: ошибка интегрирования с помощью метода Рунге-Кутты четвёртого порядка меньше ошибки интегрирования при использовании метода Рунге-Кутты второго порядка и обусловлено это не только тем, что она обратно пропорциональна величине шага в четвёртой, а не во второй степени, но и оттого, что коэффициент пропорциональности при этом существенно меньше.
Метод Рунге-Кутты четвёртого порядка имеет значительно меньшую ошибку вычисления, нежели метод Рунге-Кутты второго порядка (при условии идентичных машинных затрат). При неизменной требуемой точности для метода Рунге-Кутты четвёртого порядка необходимы меньшие затраты машинного времени относительно метода Рунге-Кутты второго порядка, отчего при корректном выборе шага интегрирования метод Рунге-Кутты четвёртого порядка значительно результативнее, чем метод Рунге-Кутты второго порядка.
|
|
|
БИБЛИОГРАФИЯ
1 Самарский А.А., Гулин А.В. Численные методы.М.: Наука, ГРФМЛ, 1989.- 432с.
2 Бахвалов Н.С. Численные методы. М.: Наука, ГРФМЛ,1987.-600 с.
3 Ляшко И.И., Макаров В.Л. Интегральные методы вычислений. Киев, 1977, 408с.
4 Мантуров О.В. Курс высшей математики М.:В.Ш.-1991.-448с.
5 Маликов В.Т. Вычислительные методы и применение Киев: В.Ш.-1989.-213 с.
ПРИЛОЖЕНИЕ А
(Справочное)
Основная программа
program DU(input,output);
uses crt;
type vector_n = array [1..2] of real;
var t0, tf, k, j, n: integer;
t, yt, h, h_screen, e2, e4, e2max, e4max, i_screen: real;
y2, y4: vector_n;
name: string;
outfile: text;
begin
clrscr;
writeln('Please enter file name');
readln(name);
writeln('Please enter h,h_screen');
readln(h,h_screen);
clrscr;
writeln;
assign(outfile,name);
rewrite(outfile);
t0:=0;
tf:=10;
n:=round((tf-t0)/h);
y2[1]:=1;
y2[2]:=0;
y4:=y2;
e2:=0;
e4:=0;
e2max:=0;
e4max:=0;
t:=t0;
i_screen:=h_screen;
for k:=0 to n do
begin
yt:=clearsolve(t);
e2:=abs(yt-y2[1]);
e4:=abs(yt-y4[1]);
if e2>e2max then e2max:=e2;
if e4>e4max then e4max:=e4;
if i_screen>h_screen-0.00001 then
begin
yt:=clearsolve (t);
e2:=abs(yt-y2[1]);
e4:=abs(yt-y4[1]);
if e2>e2max then e2max:=e2;
if e4>e4max then e4max:=e4;
if i_screen>h_screen-0.00001 then
begin
writeln(' t=',t:6:3,'; yt=',yt:9:3,'; y2=',y2[1]:9:3,'; y4=',y4[1]:9:3,'; e2=',e2:6:3,'; e4=',e4:8:6);
writeln(outfile,' t=',t:10:6,'; yt=',yt:10:6,'; y2=',y2[1]:10:6,'; y4=',y4[1]:10:6,'; e2=',e2:12:9,'; e4=',e4:12:9,'.');
i_screen:=0;
end;
if t+h>tf-0.000001 then
begin
h:=tf-t;
t:=tf-h;
i_screen:=h_screen;
end;
RK2(t,h,y2);
RK4(t,h,y4);
t:=t+h;
i_screen:=i_screen+h;
end;
writeln;
writeln(' h=',(h):8:5,'; e2max=',e2max:16:8,'; e4max=',e4max:16:8,' ',n:8);
writeln(outfile);
writeln(outfile,' h=',h:6:5,'; e2max=',e2max:10:8,'; e4max=',e4max:10:8,'.');
close(outfile);
readkey;
end.
Функция вычисления точного решения
function clearsolve(t:real):real;
begin
clearsolve:=exp(-t)*(cos(t)+sin(t)+t*sin(t));
end;
|
|
|
