 |
Оптимизация стропильной конструкции
|
|
|
|
Методические указания. Программная система АОС-ЖБК [11] позволяет выполнить оптимизацию проектируемой стропильной конструкции по критерию относительной стоимости стали и бетона, при этом за единицу автоматически принимается относительная стоимость рассчитанного студентом варианта по индивидуальному заданию.
Варьируемыми параметрами могут быть: тип стропильной конструкции и соответствующие типы опалубочных форм, классы бетона, классы ненапрягаемой и напрягаемой арматуры.
1.4 Проектирование колонны:
Таблица 3. Определение основных сочетаний расчетных усилий в сечении 3-3 колонны по оси Б.
| № | Загружения и усилия | Расчетное сочетание усилий (силы – в кН; моменты – в кН/м) | ||||
| N Mmax | N Mmin | Nmax Mmax (Mmin) | Nmin Mmax (Mmin) | |||
| загруженния | 1+(10+18)*0,85 | 1+(6+12)*0,7+14*0,85 | 1+2+(6+12)*0,7+ +14*0,85 | 1+(6+12)*0,7+14*0,85 | ||
| 1 | У С И Л И Я | N | 248,89 | 248,89 | 324,49 | 248,89 |
| M | 47,0835 | -97,289 | -90,059 | -90,059 | ||
| N1 | 248,89 | 248,89 | 324,49 | 324,49 | ||
| M1 | 11,29 | 11,29 | 18,52 | 18,52 | ||
| Nsh | 0 | 0 | 0 | 0 | ||
| Msh | 35,7935 | -108,58 | -108,58 | -108,58 | ||
| загруженния | 1+(2+(10+18)*0,85+22)*1 | 1+((6+14)*0,85+23)*0,9 | 1+(2+(6+14)*0,85+23)*0,9 | 1+((6+14)*0,85+23)*0,9 | ||
| 2 | У С И Л И Я
| N | 316,93 | 248,89 | 316,93 | 248,89 |
| M | 52,4951 | -94,09 | -87,58 | -94,09 | ||
| N1 | 248,89 | 248,89 | 248,89 | 248,89 | ||
| M1 | 11,29 | 11,29 | 11,29 | 11,29 | ||
| Nsh | 68,04 | 0 | 68,04 | 0 | ||
| Msh | 41,2051 | -105,38 | -98,87 | -105,38 | ||
Размеры сечения надкрановой части колонны b=400 мм, h=600 мм. Назначаем для продольной арматуры а=а'=40 мм, тогда h0=h–а=600–40=560 мм.
Определим сначала площадь сечения продольной арматуры со стороны менее растянутой грани (справа) при условии симметричного армирования от действия расчетных усилий в сочетании N и Мmin:
N = 248,89 кН, М = | Mmin | = 97,289 кН·м;
N l = 248,89 кН, М l = 11,29; Nsh = 0; Мsh = 108,58 кН·м.
Поскольку имеются нагрузки непродолжительного действия, то вычисляем коэффициент условий работы бетона γ bl согласно п. 3.1 [3]. Для этого находим: момент от действия постоянных, длительных и кратковременных нагрузок (кроме нагрузок непродолжительного действия) относительно оси, проходящей через наиболее растянутый (или менее сжатый) стержень арматуры:
|
|
|
MI=(N – Nsh)(h0 - а')/2 + (М – Msh) = (248,89-0) (0,56-0,04) / 2+ (97,289-108,581)= 53,42 кНм;
то же, от всех нагрузок
MII=N(h0 –а')/2+М= 248,89(0,56–0,04) / 2 + 97,289 = 162,0004 кНм.
Тогда при γb2 =0,9 получим γ bl = 0,9МП/МI = 0,9·162 /53,42= 2,73>1,1.
Принимаем уы = 1,1 и Rb = 1,1·19,5 = 21,45 МПа.
Расчетная длина подкрановой части колонны при учете нагрузок от кранов равна l 0= 12,375 м (см. табл.1). Так как l 0/h=12,375/0,6=6,5>4, то расчет производим с учетом прогиба элемента, вычисляя Ncr по формуле (93) [3]. Для этого находим е0 = M/N=97,28·106/(248,89·103) =390,89 мм > еа = h/30=600/30=20 мм; так как е0/h= 390,9/700=0,55 > δe,min=0,5–0,01· l 0/h–0,01Rb=0,2205, принимаем δe = e 0/h=0,55.
Поскольку изгибающие моменты от полной нагрузки и от постоянных и длительных нагрузок имеют разные знаки и е0=390,89 мм>0,1h=70 мм, то принимаем φl=1.
С учетом напряженного состояния сечения (малые эксцентриситеты при больших размерах сечения) возьмем для первого приближения коэффициент армирования μ=0,004, тогда при а=Еs/Еb=190 000/32 500=5,85 получим:
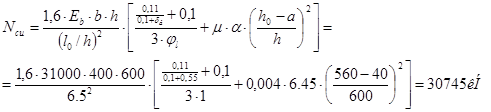
Коэффициент η будет равен: η= 1/(1–N/ Ncr)=l / (1–248,89/30745)=1,008.
Вычислим значение эксцентриситета с учетом прогиба элемента по формуле:
е=е0η+(hо—а'}/2= 390,8· 1,008+ (560—40)/2=653,12 мм.
Необходимое продольное армирование определим согласно п. 3.62 [3]. По табл. 18 [3] находим ξR=0,519 и αR=0,384.
Вычислим значения коэффициентов:
αn=N/(Rbbh0)=248,89·103/(21,45 • 400 ×560)=0,0518;
αm1= Ne /(R bh02)=248,89·103 • 653/(21,45 • 400 • 5602)= 0,0604;
б=а'/h0= 40/560=0,0714.
Так как αn < ξR, значения A=A'S определяем по формуле
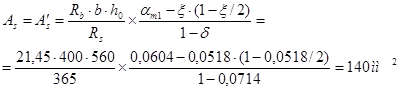
Поскольку по расчету арматура не требуется, то сечение ее назначаем в соответствии с конструктивными требованиями табл. 47 [3]: A=A'S= 0,002bh0=0,002·400·560=448 мм2.
|
|
|
Тогда получим (A=(As+A's)/(M)=(448+448)/(400·600)=0,0044, что незначительно отличается от предварительно принятого μ=0,004, следовательно,расчет можно не уточнять, а окончательно принять Ssn=As=448 мм2.
Определим площадь сечения продольной арматуры со стороны наиболее растянутой грани (слева) для несимметричного армирования с учетом, что со стороны сжатой грани (справа) должно удовлетворяться условие A's≥AS,fact =Asn=448 мм2 (по предыдущему расчету). В этом случае расчетные усилия возьмем из сочетания N и Мmin.
Вычислим коэффициент γ bl:, MI=(356,75–75,6)(0,56–0,04)/2+(17,22-6,18)= 62,1кНм; MII=356,75(0,56–0,04)/2+17,22= 110 кНм; γb2 =1 получим γ bl = 0,9МП/МI=0,9·110/62,1= 1,6>1,1. Принимаем уы = 1,1 и Rb = 1,1·19,8 = 21,78 МПа. кН • м.
η=l/(l–356,75/4958,4)=1,08.
Вычисляем е0 = М / N=17,22·106/(356,75·103)=48,26 мм, тогда e=e0η+(h0-a')/2=48,26· ·1,08+(566—40)/2==312,1 мм.
Площади сечения сжатой и растянутой арматуры определяем согласно п. 3.66 [3].
Тогда получим:

Поскольку по расчету арматура не требуется, то сечение ее назначаем в соответствии с конструктивными требованиями табл. 47 [3]: A=A'S= 0,002bh0=0,002·400·560=448 мм2.
Конструирование продольной и поперечной арматуры колонны с расчётом подкрановой консоли: анализируя результаты расчета всех опасных сечений колонны, целесообразно в надкрановой части принять симметричную продольную арматуру по 2 ø 18 А-III (ASл=Asn=509 мм2>448 мм2).
В подкрановой части колонны наиболее опасным будет сечение 4-4, 5-5, 6-6, для которого у левой грани принимаем продольную арматуру из 2ø20 А-III(ASл=Asn=628мм2>608 мм2).
Поперечную арматуру в надкрановой и подкрановой частях колонны по условию свариваемости принимаем диаметром 5 мм класса Вр-I, которая должна устанавливаться в сварных каркасах с шагом 300 мм (не более 20d=20·18=360 мм).
Выполняем проверку принятого продольного армирования на прочность в плоскости, перпендикулярной раме, при действии максимальных продольных сил.
Для над крановой части колонны имеем: N=324,49 кН; N,=248,89 кН; Nsh=0. Поскольку нет нагрузок непродолжительного действия, то расчетные сопротивления бетона принимаем с γb2=1 (при заданной влажности 80 %). Размеры сечения: b=600мм, h=400 мм. Назначая а=а'=40 мм, получим h0=h-а=400-40=360 мм. Расчетная длина над крановой части колонны l 0=5,85 м (см. табл. 2.1). Так как /0/h=5850/400=14,625>4, то необходимо учесть влияние прогиба элемента на его прочность.
|
|
|
Находим значение случайного эксцентриситета:
еа>h/30=400/30=13,33мм; еа>H2/600=3900/600=6,5мм; еа>10мм. принимаем еа=13,33мм. Тогда соответствующие значения изгибающих моментов будут равны:
М= N·еа =324,49·103·13,33=4,325·106Нмм= 4,325 кНм;
М l = N l·e а=248,89·103·13,33=3,12·106 Нмм=3,12 кНм.
Для определения Ncr вычисляем:
M1 l = Nl ·(h 0 —а')/2+М l =248,89(0,36-0,04)/2+3,12=43,07 кН·м;
Ml=N(h0—a')/2+M=324,49(0,36-0,04)/2+4,325=56,2434 кНм;
φl=1+(1·43,07)/56,2434= 1.7658<2;
μ=(As+А's)/(bh)=(509+509)/(600·400)=0,00424;
так как ea/h=13,33/400=0,0333<δemin=0,5-0,01·14,625–0,01·19,5=0,158, принимаем δe=δemin=0,156.
Тогда:
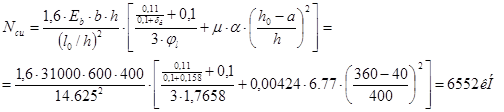
е=еаη+(h0—а')/2= 13,33 · l,0521+(360—40)/2= 174,0245 мм.
Проверку прочности сечения выполняем по формулам пп. 3.61 и 3.62 [3]. Определяем x=N/(Rbb)=324,49·103/(19,5-600)=27,73 мм. Так как x<ξR·h0=0,519·360=186,84 мм, то прочность сечения проверяем по условию (108) [3]:
Rbbx(h0–0,5х)+Rsc·A´s(h0-а')=19,5·600·27,73(360–0,5·27,73) +280·509 (360-40) = =157,9·106 Н·мм =157,9 кНм > Ne = 324,42·0,174 = 56,47 кН·м, т. е. прочность надкрановой части колонны в плоскости, перпендикулярной поперечной раме, обеспечена
При проверке прочности подкрановой части колонны в плоскости, перпендикулярной плоскости изгиба, учитываем только угловые стержни по 2 ø20 А-III (As=A's=628мм2). В этом случае имеем размеры сечения: h=700мм, a=400мм и расчетную длину l 0=6,6 м (см. табл. 2.1). Так как l 0/h=6600/400=16,5>4, то необходимо учесть влияние прогиба элемента на его прочность, а расчетными усилиями в сечении 6 — 6 будут: N=851,25 кН; N l =397,6 кН; Nsh=385,62 кН.
Находим значение случайного эксцентриситета: еа>h/30=400/30=13,33 мм; еа>H2/700=7560/700=10.08 мм; еа>10 мм. Принимаем еа=13,33 мм. Тогда соответствующие значения изгибающих моментов будут равны:
М= N·еа =922,6·103 ·13,33=12,29·106 Нмм= 12,29 кНм;
М l =N l·e а=468,94 ·103·13,33=6,25·106 Нмм=6,25кНм.
Для определения Ncr вычисляем:
M1 l = Nl ·(h 0 -а')/2+М l =468,94(0,36-0,04)/2+6,25=81,3кНм;
Ml=N(h0-a’)/2+M=922,6(0,36-0,04)/2+12,29=160 кНм;
φl=1+(1·81,3)/160= 1,51<2;
μ=(As+А's)/(bh)=(509+509)/(800·400)=0,00477; так как
ea/h=13,33/400=0,0333<δemin=0,5-0,01·18.9–0,01·19,8=0,113, принимаем δe=δemin=0,113.
Тогда:
 '.
'.
е=еаη+(h0—а')/2= 13,33·1,148+(360—40)/2= 175,3 мм.
Проверку прочности сечения выполняем по формулам пп. 3.61 и 3.62 [3]. Определяем
|
|
|
x=N/(Rbb)=922,6·103/(19,8·800)=58,2мм.
Так как x<ξR·h0=0,582·360=209,5мм, то прочность сечения проверяем по условию (108) [3]:
Rbbx(h0–0,5х)+Rsc·A´s(h0-а')=19,8·800·58,2(360-0,5·58,2) +365·763(360-40)=394,17·106Нмм =394,17 кНм > Ne = 922,6·0,1753 = 161,7 кНм, т. е. прочность надкрановой части колонны в плоскости, перпендикулярной поперечной раме, обеспечена.
Расчет прочности подкрановой консоли производим на действие нагрузки от собственного веса подкрановых балок и максимального вертикального давления от двух сближенных мостовых кранов с учетом коэффициента сочетаний ψ=0,85, или Q = G6+Dmaxψ = 48,4+504,1·0,85 = 476,89 кН (см. раздел 2.1).
Проверяем прочность консоли на действие поперечной силы при возможном разрушении по наклонной полосе в соответствии с п. 3.99 [3]. Поскольку 2,5Rbt·b·h0 = 2,5·1,3·400·1060 = =1378·103 Н=1378 кН > Q = 476,89 кН, то по расчету не требуется поперечная арматура. По конструктивным требованиям принимаем хомуты диаметром 6 мм класса A-I, устанавливаемые с максимально допустимым шагом 150 мм.
Для обеспечения прочности консоли в вертикальном сечении на действие изгибающего момента определяем площадь сечения продольной арматуры по формуле (208) [3]:
As=Q l 1 /(h0Rs)=476,89·103·450/(1060·280)=723,3мм2. Принимаем 3 ø 16 А-III (A5=763мм2).
1.5 Проектирование монолитного внецентренно-нагруженного фундамента:
Для предварительного определения размеров подошвы фундамента находим усилия Nnf и Mnf на уровне подошвы фундамента для комбинации усилий с максимальным эксцентриситетом с учетом нагрузки от ограждающих конструкций.
Расчетная нагрузка от стеновых панелей и остекления равна G3=35,7192 кН (см. раздел 2.1), а для расчета основания Gn3 = G3/γf = 35,7192/1,1 = 32,472 кН. Эксцентриситет приложения этой нагрузки относительно оси фундамента будет равен е3 = 240/2+400 = 520мм = 0,52м.
Анализируя значения усилий в таблице находим, что наиболее неблагоприятной комбинацией для предварительного определения размеров подошвы фундамента по условию максимального эксцентриситета (отрыва фундамента) является вторая комбинация усилий. В этом случае получим следующие значения усилий на уровне подошвы фундамента:
Nfn= Nn + Gn3 = 474,56+32,472 = 507,032 кН;
Мfn=Мп + Q·hf +G3n· е 3 = -225,61-29,36·2,4-32,47·0,52= -312,949 кН·м;
e 0 = | Мfn / Nfn| = 312,1/575,21 = 0,54 м.
С учетом эксцентриситета продольной силы воспользуемся формулами табл. XII.I. [1] для предварительного определения размеров подошвы фундамента по схеме 2:
 м
м
 м
м
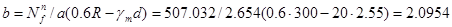 м
м
где γm= 20 кН/м — средний удельный вес фундамента с засыпкой грунта на его обрезах; R= R0 = 0,3 МПа = 300 кПа - условное расчетное сопротивление грунта по индивидуальному заданию.
Принимаем предварительно размеры подошвы фундамента, а =2,7 м и b=2,1 м. Уточняем расчетное сопротивление песчаного грунта основания согласно прил. 3 [9]:
|
|
|
R=R0[1+k1(b– b0)/b0]+ k2·γm(d -d0)=250·(1+0,125·(2,1-1)/1)+0,25·20(2,55-2)=287,125кПа,
где k1 = 0,125 и ki = 0,25 принято для песчаных грунтов по [9].
Определим усилия на уровне подошвы фундамента принятых размеров от нормативных нагрузок и соответствующие им краевые давления на грунт по формулам:
Nninf= Nn + Gn3 +a·b·d·γm·γn; Мninf=Мп + Q·hf +G3n· е 3; Pnл(п)= Nninf/Af±Мninf/Af: где γm =1 - для класса ответственности здания I; Af= ab = 2,7·1,8 =5,67 м2;Wf = ba2/6 = 1,8·2,72/6=2,552 м3.
Таблица 2. Постоянные нагрузки на 1 м² покрытия:
| Комбинация усилий от колонны | Усилия | Давление к.Па. | |||
| Мninf | Nninf | Pnл | Pnп | Pnm | |
| Первая | 943,522 | 46,95 | 148,005 | 184,807 | 166,406 |
| Вторая | 796,202 | -312,949 | 263,077 | 17,771 | 140,424 |
| Третья | 1061,862 | -212,378 | 270,514 | 104,041 | 187,277 |
Так как вычисленные значения давлений на грунт основания:
Рnmах =270,514кПа < l,2R = 1,2·287,125 = 344,55 кПа;
Pnmin = 17,771 кПа > 0;
Pnm= 187,277 кПа < R = 287,125 кПа;
то предварительно назначенные размеры подошвы фундамента удовлетворяют предъявляемым требованиям по деформациям основания и отсутствию отрыва части фундамента от грунта при крановых нагрузках. Таким образом, оставляем окончательно размеры подошвы фундамента а = 2,7 м и b = 2,1 м.
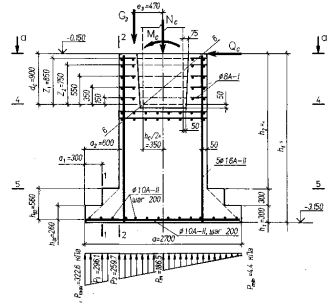
Расчет тела фундамента выполняем для принятых размеров ступеней и стакана согласно рисунку. Глубина стакана назначена в соответствии с типом опалубки колонны по приложению V, а поперечное сечение подколенника имеет размеры типовых конструкций фундаментов под колонны промышленных зданий.
Расчет на продавливание ступеней фундамента не выполняем, так как размеры их входят в объем пирамиды продавливания.
Для расчета арматуры в подошве фундамента определяем реактивное давление грунта основания при действии наиболее неблагоприятной комбинации расчетных усилий (третьей) без учета собственного веса фундамента и грунта на его обрезах. Находим соответствующие усилия на уровне подошвы фундамента:
Ninf= Nc + G3 = 851,25+35,7192 = 886,9692 кН;
Minf= Мc + G3е3 + Qcht = -142,63-35,7192·0,52-39,23·2,4 = -255,356 кНм.
Тогда реактивные давления грунта будут равны:
ршах = 886,9692/5,67 + 255,356/2,5515 = 256,5127 кПа
ршin = 886,9692/5,67 - 255,356/2,5515 = 56,3512 кПа
Р 1 = р m ах – (р m ах – pmin/a)·a1 = 256,5127 – (256,5127 – 56,3512)/2,7 · 0,3 = 234,27258 кПа;
Р2 = 212,0324 кПа;
Расчетные изгибающие моменты в сечениях 1 – 1, 2 – 2 и т.д. вычисляем по формуле:
М1-1 = b ·а i 2 ·(2·р m ах + pi)/6 = 2,1 · 0,32(2 · 256,5127+234,2725)/6 = 23,539 кНм;
М 2-2 = 2,1 · 0,62(2 · 256,5127+212,0324)/6 = 91,3572 кНм.
Требуемое по расчету сечение арматуры составит:
As,1-1= Ml-1/(Rs·0,9·h01) =23,54·106/(280·0,9·260) = 359,2643 мм2
As,2-2= M2-2/(Rs·0,9·h02) = 91,3572·106/(280·0,9·560) = 647,3724 мм2;
Принимаем минимальный диаметр арматуры для фундамента при а =2,7 м равным 10 мм. Для основного шага стержней в сетке 200 мм на ширине b = 2,1 м будем иметь в сечении 2–2 9 ø 10, А-III, As = 707 мм2 > 647,37 мм2. Процент армирования будет равен μ =А s ·100/(b · h 04) = =647,37·100/(1800·560) = 0,06 % > μmin = 0,05 %.
Расчет рабочей арматуры сетки плиты фундамента в направлении короткой стороны выполняем на действие среднего реактивного давления грунта рт = 270,053 кПа, соответственно получим:
М3–3= pm · a · b12/2 =156,43·2,7·0,32/2 = 19,0062 кНм;
As ,3–3 = M 3–3 /(Rs ·0,9· h 0) = 19,0062·106/(280·0,9·250) = 301,6857 мм2.
По конструктивным требованиям принимаем минимальное армирование 14ø10, А - III, с шагом 200мм.
Расчет продольной арматуры подколенника выполняем в ослабленном коробчатом сечении 4–4 в плоскости заделки колонны и на уровне низа подколонника в сечении 5–5. Размеры коробчатого сечения стаканной части фундамента преобразуем к эквивалентному двутавровому с размерами, мм: b = 650; h = 1500; bf = b ' f = 1200; hf = h ' f = 300; а = а´ = 50; h 0 = 1450. Вычислим усилия в сечении 4 – 4 от второй комбинации усилий в колонне с максимальным изгибающим моментом по следующим формулам:
N =Nc+G3 +ac·bc·dc·γ·γm·γп=545,75 + 35,7192+1,5·1,2·0,9·25·1,1·1 = 626,0192 кН
M =Mc+Qc·dc+G3·е3= 259,45 + 33,76·0,9 + 35,7192·0,52 = 308,408 кН*м.
Эксцентриситет продольной силы будет равен:
e0=M/N=308,4082/626,0192 = 0,493м = 493 мм > еа = h /30 = 1500/30 = 50 мм.
Находим эксцентриситет силы N относительно центра тяжести растянутой арматуры:
e = eо +(hо – a´)/2 =493 + (1450 – 50)/2 = 1193мм.
Проверяем положение нулевой линии. Так как Rb·b´f·h´f = 11,5·1200·300 = 4140·103 Н = =4140 кН >N= 626,0192 кН, то указанная линия проходит в полке и сечение следует рассчитывать как прямоугольное с шириной b = b'f = 1200 мм. Расчет прочности сечения для случая симметричного армирования выполняем согласно п. 3.62 [3]. Вычисляем коэффициенты:
αn=N/(Rb·b·h0)=626,0192·103/(11,5·1200·1450)=0,0313;
αm1= N·е/(Rb·b·h02) = 626,0192·10³·1193/(11,5·1200·14502) = 0,0257;
δ = а'/h0 = 0,0345.
Требуемую площадь сечения продольной арматуры вычислим по следующей эмпирической формуле:
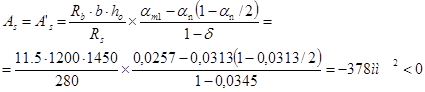
Армирование назначаем в соответствии с конструктивными требованиями в количестве не менее 0,05 % площади подколонника: As = A ' s = 0,0005·1200·1500 = 900 мм2. Принимаем As = A ' s = 1005 мм2 (5 ø 16 А-III).
В сечении 5–5 по аналогичному расчету принято конструктивное армирование.
Поперечное армирование стакана фундамента определяем по расчету на действие максимального изгибающего момента. Вычисляем эксцентриситет продольной силы в колонне от второй комбинации усилий е0 = Mc / Nc = 259,45/545,75 = 0,4754 м. Поскольку е o = 0,4754 м > h с /6 = 0,8/6 = 0,1333 м, то поперечная арматура стакана требуется по расчету. Так как е o = 0,4754 м > hc /2 = 0,4 м, то момент внешних сил в наклонном сечении 6–6 вычисляем по формуле:
M 6–6 = Mc + Qc · dc – 0,7 · Nc ·е o = 259,45 + 33,67·0,9 – 545,75·0,4 = 71,534 кНм.
Тогда площадь сечения одного стержня поперечной арматуры стакана фундамента будет равна:
А s = М6–6/(4 · Rs · Σ zi) = 71,534 · 106/[4 · 225(850+750+550+350+150)] = 29,9932мм2.
Принимаем As = 50,3 мм2 5ø8 A-III).
 |
Список используемой литературы.
1. Байков В.Н., Сигалов Э.Е. Железобетонные конструкции. Общий курс. М.; Стройиздат, 1985.
2. СНиП 2.03.01-84. Бетонные и железобетонные конструкции. М.; ЦИТП, 1985.
3. Пособие по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры (к СНиП 2.03.01-84). М.; ЦИТП, 1986.
4. Пособие по проектированию предварительно напряженных железобетонных конструкций из тяжелых и легких бетонов (к СНиП 2.03.01-84). Ч.1. М.; ЦИТП, 1986.
5. Пособие по проектированию предварительно напряженных железобетонных конструкций из тяжелых и легких бетонов (к СНиП 2.03.01-84). Ч.2. М.; ЦИТП, 1986.
6. СНиП 2.03.01-84.Нагрузки и воздействия. М.; ЦИТП, 1987
7. СНиП 2.03.01-84.Основания зданий и сооружений/Госстрой СССР. М.;Стройиздат, 1985.
8. Бородачев Н.А. Автоматизированное проектирование ЖБК одноэтажных промышленных зданий. Методические указания.
|
|
|


