 |
Алгебры с одной бинарной алгебраической операцией
|
|
|
|
Это – полугруппы, моноиды, группы. Пусть А ≠ Æ.
def. Множество с заданной на нем одной ассоциативной бинарной операцией называется полугруппой.
def. Полугруппа с нейтральным элементом называется моноидом.
def. Если заданная бинарная операция еще и коммутативна, то полугруппа, или моноид, называется коммутативной (абелевой).
Итак, в полугруппе может не существовать обратный элемент и даже нейтральный элемент. В моноиде обязательно есть нейтральный элемент, но может не быть обратного.
def. Алгебра А = < А, 
> называется группой, если она есть моноид, в котором каждый элемент обратим.
Алгебр структуры. Алгебры с двумя бинарной алгебраической операцией
def. Алгебра А = < А, +,∙ > называется ассоциативным кольцом с единицей (или кратко кольцом), если выполняются следующие условия:
1.Алгебра < A,+ > - коммутативная (абелева) аддитивная группа;
2.Алгебра < A, ∙ > - мультипликативный моноид;
3.Операция умножение дистрибутивна относительно сложения, то есть
a.
def. Кольцо А = < А, +,∙ > называется коммутативным, если операция умножения коммутативна: 
.
Алгебра < Z,+,∙ > - коммутативное кольцо.
def. Коммутативное кольцо с единицей, в котором каждый ненулевой элемент обладает обратным относительно операции умножения, называется полем.
Алгебры с 1 и двумя бинарной алгебраической операцией
I. Это – полугруппы, моноиды, группы. Пусть А ≠ Æ.
def. Множество с заданной на нем одной ассоциативной бинарной операцией называется полугруппой.
def. Полугруппа с нейтральным элементом называется моноидом.
def. Если заданная бинарная операция еще и коммутативна, то полугруппа, или моноид, называется коммутативной (абелевой).
|
|
|
Итак, в полугруппе может не существовать обратный элемент и даже нейтральный элемент. В моноиде обязательно есть нейтральный элемент, но может не быть обратного.
def. Алгебра А = < А, > называется группой, если она есть моноид, в котором каждый элемент обратим.
II. def. Алгебра А = < А, +,∙ > называется ассоциативным кольцом с единицей (или кратко кольцом), если выполняются следующие условия:
1.Алгебра < A,+ > - коммутативная (абелева) аддитивная группа;
2.Алгебра < A, ∙ > - мультипликативный моноид;
3.Операция умножение дистрибутивна относительно сложения, то есть
a.
def. Кольцо А = < А, +,∙ > называется коммутативным, если операция умножения коммутативна: .
Алгебра < Z,+,∙ > - коммутативное кольцо.
def. Коммутативное кольцо с единицей, в котором каждый ненулевой элемент обладает обратным относительно операции умножения, называется полем.
Конечные поля
Наряду с бесконечными полями имеются конечные поля, Конечные поля играют центральную роль в криптографии в математических моделях микромира. Определим сравнимость целых чисел по модулю m.
def. Пусть Z – множество целых чисел. Назовем два числа x и y из Z сравнимыми по модулю m (m 
) и запишем xºy(mod m), если равны остатки этих чисел от деления на m, то есть разность (x-y) делится на m.
Отношение “сравнимых по модулю m целых чисел” есть отношение эквивалентности на множестве целых чисел Z, т.к отношение 1.рефлексивно, 2.транзитивно,
3. симметрично Отношение эквивалентности º определяет разбиение множества Z на m подмножеств – классов эквивалентности, 
. Обозначим фактор – множество 
через 
def. Введем на 
= 
операции следующим образом:
+ 
= 
– сложение; ∙ = 
- умножение.
если х1º х (mod m), y1ºy (mod y), то
х1+у1 º (х+у) (mod m) и x1∙y1 º x 
y (mod m).
Далее < 
,+,∙ > есть коммутативное кольцо. Тогда имеем ∙ 
= 
∙ 
= 
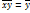для 
Кольцо Zm называется кольцом вычетов по модулю m. Теорема. Кольцо Zm является полем тогда и только тогда, когда m - простое число.
|
|
|
Гомоморфизмы алгебры
def. Пусть Аи В – однотипные алгебры, fa- главная операция алгебры A, а fb – соответствующая ей главная операция алгебры B, (т.е.f a и f b имеют одинаковые ранги).
, где n – ранг операции 
(n1,n2,…,ns) – тип алгебры A
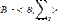
(n1,n2,…,ns) – тип алгебры B
def. Отображение h основного множества А в основное множество В, сохраняет главную операцию f a алгебры A, если для (
)
, где n – ранг операции 
. (
)
def. Гомоморфизмом алгебры A в (на) однотипную алгебру B называют такое отображение h множества Aв (на) множество B, которое сохраняет все главные операции алгебры A, т.е. для любой операции fa алгебры A выполняется условие ().
def. Гомоморфизм алгебры A на алгебру B называется эпиморфизмом.
def. Гомоморфизм h алгебры A на алгебру B называют изоморфизмом, если h есть инъективное отображение множества A на множествo B. При этом пишут 
.
def. Гомоморфизм h алгебры A в алгебру B, называется мономорфизмом, если h является инъективным отображением множества A в множество B.
def. Гомоморфизм алгебры Aв себя, называется эндоморфизмом.
def. Изоморфизм алгебры A на себя, называется автоморфизмом.
Алгебраические системы
def. Упорядоченная тройка 
называется алгебраической системой, где
– множество алгебр. операций на А,
- мн-во отношений на множестве А.
Таким образом, алгебры можно считать частным случаем алгебраических систем. Другим частным случаем алгебраических систем являются модели – множества, на которых заданы только отношения.
Решетки
def. Решёткой называется частичное упорядоченное множество 
, в котором каждая пара элементов имеет sup и inf. Для заданных элементов 
элемент inf{x,y}называется пересечением элементов х и у (обозначается 
), а sup{x,y} называется объединением элементов х и у (обозначается 
), Решетка – это алгебраическая система
где 
- бинарные операции на множестве A, 
- бинарное отношение частичного порядка на A.
Заметим, что если в системе A введены операции , то отношение 
можно по этим операциям восстановить следующим образом:
, а также
Наименьший (наибольший) элемент решетки, если он существует, называют
нулем (единицей). Обозначаются эти элементы соответственно через 0 и 1.
|
|
|
Пример 1. Любое конечное линейно упорядоченное множество является решеткой. Пример 2. Рассмотрим 
, в котором 
, а элементы 
. Система A образует решётку, В этой решётке a=0, e=1
 |
58. Матроиды. Жадн. Алгоритмы Матроид является классиф-ей подмножеств конечного мн-ва, предст. собой обобщение идеи независимости элементов. Матроид – упорядоченная пара <X,I> где X-конечное мн-во (носьтель матроида) Y-некоторое мн-во подмн-в X семейства независимых множеств (I включено в P(I)) При этом 1. 
2. Есл. 
и 
, то 
3.Если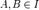 
и мощность A больше мощности B, то существует 
такой, что 
Базами матроида называются максимальные по включению независимые множества Минимальные по включению зависимые множества называются циклами матроида Свободный матроид: <X,P(x)> Жадный алгоритм Опр: Жадный алгоритм — алгоритм, заключающийся в принятии локально оптимальных решений на каждом этапе, допуская, что конечное решение также окажется оптимальным. Общего критерия оценки применимости жадного алгоритма для решения конкретной задачи не существует, однако, для задач, решаемых жадными алгоритмами, характерны две особенности: во-первых, к ним применим Принцип жадного выбора, а во-вторых, они обладают свойством Оптимальности для подзадач
|
|
|
