 |
Найти количество полос на экране, определяемое геометрией, системы
|
|
|
|
Для расчета ширины интерференционных полос сведем схему с билинзой к схеме Юнга. Для этого вычислим расстояние между изображениями источника света, давемыми половинками билинзы. Воспользуемся формулой линзы:
Мы полагаем расстояния a и b положительными. Поскольку в формуле линзы фигурируют координаты предмета и изображения, которые слева от линзы отрицательны, в формулу расстояния подставлены со знаком минус. Если источник находится в фокальной плоскости билинзы, то мнимые изображения его оказываются в бесконечности (b=∞).
Расстояние между изображениями источника – d найдем из подобия треугольников S1S2S и O1O2S:
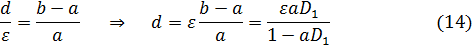
Зададим произвольно расстояние l между экраном и линзой. Ширина полос определится формулой для схемы Юнга:
Формула для ширины полосы становится очень простой, если источник расположить в фокальной плоскости билинзы, т.е. взять, а=f1. В этом случае
Т.е. ширина полосы не зависит от расстояния между линзой и экраном. Это естественно, поскольку когерентные источники света находятся в бесконечности, а лучи от них параллельны оси симметрии и перпендикулярны экрану.
Ширина области перекрытия интерферирующих потоков на экране - |MK| определится из подобия треугольников SMK и SO2O1:
Отношение |MK|/Δх дает число интерференционных полос:
Вместо оптической силы D1 использовано фокусное расстояние f`1=1/D1. Эта формула записана таким образом, что первый сомножитель (перед квадратной скобкой) состоит только из заданных в условии величин, а второй множитель зависит от величин l и a, которые можно задать самостоятельно. В частном случае, когда a=f1, т.е. aD1=1, будем иметь:
Зададим, наконец, расстояния от билинзы до источника a=f1=0.273 м и расстояние от билинзы до экрана l=9a=2.457 м. Такой выбор расстояний позволить вычислить ширину полосы и число полос по простым формулам (16) и (19). После подстановки числовых данных получим:
|
|
|
Т. Е. на экране буде т видна центральная полоса и еще по две полосы с двух сторон (всего 5 штук).
Задание 5 выполнено.
6.
| Рисунок 5 |
На систему из двух длинных прямоугольных щелей, показанных на рис. 5, падает нормально свет с длиной волны λ. Пусть I0' – интенсивность света, наблюдаемого в направлении первоначального распространения в отсутствие среднего непрозрачного промежутка шириной b1. Найти отношение интенсивности света, наблюдаемого в направлении, определяемом углом φ, к I0'. При φ<0 угол откладывается от вертикали по часовой стрелке.
Будем использовать метод суммирования колебаний с помощью суммирования векторов, изображающих колебания. Если световой поток падает перпендикулярно на узкую щель, то во всех точках щели фаза световых колебаний одинакова.
При суммировании векторов колебаний, переносимых волнами, идущими в первоначальном направлении, все векторы оказываются направлены одинаково и в сумме дают вектор того же направления, как показано на рисунке 9
Если рассматривать волны, распространяющиеся под углом φ по отношению к первоначальному направлению, то появляется разность хода между волнами от соседних элементов щели и векторная сумма закручивается в дугу окружности, показанную на рисунке 10. Угол, на который закручивается дуга, равен разности фаз волн от крайних элементов щели. Эта разность фаз выражается формулой
Где d – ширина щели. При этом угол β который составляет вектор суммы с горизонтальной осью, оказывается равным α/2. Длина дуги, представляющей векторную сумму остается неизменной и равной длине отрезка векторной суммы при φ=0. Нам задана интенсивность света, проходящего в направлении φ=0, при величине щели, равной a+b+c (см. рисунок 2). Так как интенсивность – это квадрат амплитуды можно определить амплитуду волны, идущей в направлении φ=0.
|
|
|
Величина А0 будет равна длине дуги на которой происходит суммирование векторов колебаний.
Если какая-то часть щели перекрыта, то из векторной суммы исключается соответствующая часть дуги.
Где d – ширина щели. При этом угол β который составляет вектор суммы с горизонтальной осью, оказывается равным α/2. Длина дуги, представляющей векторную сумму остается неизменной и равной длине отрезка векторной суммы при φ=0. Нам задана интенсивность света, проходящего в направлении φ=0, при величине щели, равной a+b+c (см. рисунок 2). Так как интенсивность – это квадрат амплитуды можно определить амплитуду волны, идущей в направлении φ=0.
Величина А0 будет равна длине дуги на которой происходит суммирование векторов колебаний.
Если какая-то часть щели перекрыта, то из векторной суммы исключается соответствующая часть дуги.
Суммарный вектор колебаний, переносимых волнами от первой щели, определится в виде хорды дуги с радиусом – r и углом α1. Процесс суммирования показан на рисунке 11. Сразу же вычислим горизонтальную и вертикальную суммарного вектора колебаний от первой щели
На первом открытом и перекрытом участке щели –b создается разность фаз
Вторая щель, с шириной – с, открывает путь волнам, которые несут колебания, соответствующие дуге в интервале углов от α2=6.02 рад. До α=9.86 рад. Суммирование колебаний этой дуги показано на рисунке 12. Вычислим координаты начально и конечной точки суммарного вектора.
Горизонтальная и вертикальная составляющие суммарного вектора будут равны:
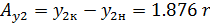
Векторы колебаний, переносимых волнами от каждой щели в направлении угла φ определены. Теперь очень просто вычислить координаты суммарного вектора:
Квадрат модуля этого вектора определяет амплитуду суммарной волны, идущей в направлении угла φ.
Но r2=I0’/α2, следовательно
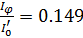Пункт 6 выполнен
7. Пусть I0'' – интенсивность света, наблюдаемого в направлении первоначального распространения при наличии среднего непрозрачного промежутка шириной b. Найти отношение интенсивности света, наблюдаемого в этом случае в направлении угла φ, к I0'
|
|
|
Для нахождения интенсивности I’’ необходимо из общей суммы векторов колебаний удалить векторы, приходящиеся на непрозрачную перегородку b. В результате длина суммарного вектора умножится на отношение ширины пропускающих щелей к общей ширине преграды (a+c)/(a+b+c). Поскольку интенсивность пропорциональна квадрату амплитуды колебаний, можем записать:
Искомое отношение будет равно
Пункт 7 выполнен.
8. На дифракционную решетку, содержащую n1 штрихов на 1мм длины, падает нормально свет с длиной волны λ. Расстояние от решетки до экрана L. Найти общее число наблюдаемых максимумов и расстояние от центрального максимума до последнего наблюдаемого. Пусть на решетку падает белый свет с длинами волн в интервале (450÷700) нм. Найти длину спектра второго порядка. Начиная со спектров каких порядков наблюдается их перекрытие?
Положение главных максимумов при дифракции на решетке определяется формулой d*sin(φ)=kλ, в которой d-период решетки, k – целое число – порядок главного максимума. Полагая φ=π/2, определим максимально возможный порядок
(Функция int(х) – взятие от дроби только целой части.)
Общее число видимых на экране главных максимумов, включая центральный будет равно 9. Четыре по обе стороны от центрального - нулевого.
Найдем угол направления на последний главный максимум
Следовательно, φmax=0.95 рад. (46.6о)
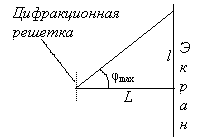
Расстояние от центрального до четвертого максимума определится из чертежа, показанного на рисунке 13
l=L*tg(φmax)=1.82 м
Предположим, что решетка освещается белым светом, λmin=450 нм,, λmax=700 нм. Тогда максимум второго порядка для фиолетовых лучей будет под углом φ1, который определится уравнением:
Максимум второго порядка для красных лучей удовлетворяет такому же уравнению:
Из этих уравнений найдем
sin(φф)=2* λmin/d=0.306 => φф=0.37 рад
sin(φкр)=2* λmax/d=0.47 => φкр=0.49 рад
Теперь определим расстояние на экране между максимумами для красных и фиолетовых лучей, это будет протяженностью спектра второго порядка
|
|
|
Δl=L(tg(φкр) – tg(φф))=0.189 м.
Дифракционная решетка отклоняет красные лучи сильнее, чем фиолетовые. Поэтому красная часть спектра k-того порядка может наложиться на фиолетовую часть k+1 порядка. В качестве условия такого наложения возьмем равенство синусов углов отклонения:
sin(φф)=(k+1)* λmin/d = sin(φкр)=k* λmax/d
Из этого равенства получим
(k+1)* λmin = k* λmax => 1+1/k=1.5555 => k=1.8
Это означает, что красная часть спектра второго порядка наложится на фиолетовую часть спектра третьего порядка.
Пункт 8 выполнен.
9. Проектируем электролампочку с вольфрамовой нитью накала. Возьмем следующие исходные данные=200 Вт, k=0.5, U=220 B, T=2400 K.
Излучаемая мощность равна поглощаемой электрической мощности. По закону Стефана – Больцмана запишем::
Где S – площадь боковой поверхности нити накала. Если l – длина нити, d – ее диаметр, то
И после подстановки площади получим:
Электрическое сопротивление нити накала выражается через длину нити и площадь ее поперечного сечения, которая равна πd2/4:
Где ρ – удельное сопротивление вольфрама, которое зависит от температуры. Данная зависимость является линейной и выражается следующей формулой:
Громоздкость этой формулы обусловлена тем, что в справочниках приводится удельное сопротивление металлов при температуре 20оС, в то время как нам необходима зависимость удельного сопротивления от абсолютной температуры (в Кельвинах). Можно немного преобразовать формулу, используя известное значение температурного коэффициента для вольфрама: α=4.8*10-3 1/К:
С учетом этой формулы сопротивление нити накала выразится следующей формулой:
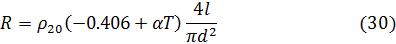
С другой стороны, сопротивление нити накала выражается через электрическую мощность:
Из двух последних равенств будем иметь следующее уравнение:
Из которого выразится длина нити:
После подстановки (33) в (27) получим уравнение для диаметра нити:
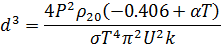
Поскольку формула получена путем множества преобразований и подстановок, необходима проверка размерности:
Размерность левой и правой части равенства совпадают, это позволяет надеется на правильность результата. Подставим числовые данные:
Подставим полученное значение диаметра в формулу для длины нити (33):
|
|
|
