|
Распределение случайной величины на основе опытных данных
|
|
|
|
Введение
Математическая статистика - наука которая занимается разработкой методов отбора, группировки и обработки опытных данных с целью изучения закономерностей массовых случайных явлений.
Математическая статистика опирается на методы и понятия теории вероятностей и, в свою очередь, служит основой для обработки анализа статистических результатов в конкретных областях человеческой деятельности.
Задачи математической статистики:
нахождение функции распределения по опытным данным.
из теоретических соображений функция распределения оказывается в общем виде известна, но неизвестны её параметры. Неизвестные параметры определяются по опытным данным.
Статистическая проверка гипотез:
в общем виде известна функция распределения, определяют её неизвестные параметры и выясняют, как согласуются экспериментальные данные с общим видом функции распределения.
Цель курсовой работы
Целью курсовой работы является закрепление теоретических знаний и приобретения навыков обработки статистической информации.
Постановка задачи
В данной курсовой работе были поставлены следующие задачи для обработки статистических данных:
построение полигона частот и относительных частот
построение гистограммы частот и относительных частот
построение эмпирической функции распределения.
нахождение выборочной средней, выборочной дисперсии и
нахождение среднего выборочного квадратичного отклонения.
5) проверка гипотезы о нормальном распределении изучаемой случайной величины.
Исходные данные
Вариант 14. Прочность на разрыв полосок ситца (в дан):
32313432312932343331313432313532
|
|
|
34333130303232343131353234333231
34323129323433313134323135323433
31303432312932343331303232313632
34333130323331283234333130323330
35323433323031333033323433313032
33303132343331303233303132333331
30323330313233303433313032333031
3233
Распределение случайной величины на основе опытных данных
Для обработки опытных данных воспользуемся составлением статистического ряда. В первой строке записываются номера наблюдений, а во второй строке результаты наблюдений.
Если результаты наблюдений расположить в возрастающем порядке, то получим вариационный ряд.
Результат измерения называется - варианта.
Число появления каждой варианты называется частотой.
Отношение частоты к объему выборки называется относительной частотой.
xi - варианта (значение, полученное в процессе измерения)
ni - частота (сколько раз появилась каждая варианта)
Р*i - отношение частоты объёму выборки
| xi | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 18 | 29 | 32 | 24 | 18 | 4 | 1 |
ni
 Pi* n Pi* n
| 1
 130 130
| 3
 130 130
| 18
 130 130
| 29
 130 130
| 32
 130 130
| 24
 130 130
| 18
 130 130
| 4
 130 130
| 1
 130 130
|
Существует вместо статистического ряда так называемая статистическая совокупность, для этого все наблюдаемые значения признака разбиваются на группы равной длины.
| xi<x≤xi+1 | (27; 29] | (29; 31] | (31; 33] | (33; 35] | (35; 37] |
| ni | 4 | 47 | 56 | 22 | 1 |
| Pi* | 4/130 | 47/130 | 56/130 | 22/130 | 1/130 |
Размах колебания: хmin=28
хmax=36
R= 36-28=8
Статистическое распределение можно изобразить графически:
Либо в виде полигона частот, полигона относительных частот и в виде гистограммы частот, гистограммы относительных частот.
Полигоном частот называется ломаная линия, соединяющая точки с абcциcсой (Ох) - варианта и ординатой (Оу) - частота.
Cтроим полигон частот.
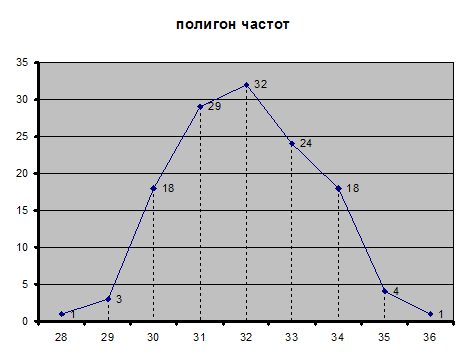
Полигоном относительных частот называется ломаная линия, соединяющая точки с абсциссой (Ох) - варианта и ординатой (Оу) - относительная частота.
Строим полигон относительных частот.
Полигон относительных частот

Гистограммой частот называется фигура, состоящая из прямоугольников с равными основаниями (длина интервала) и площадью численно равной частоте.
|
|
|
Для построения гистограммы воспользуемся таблицей:
| xi<x≤xi+1 | (27; 29] | (29; 31] | (31; 33] | (33; 35] | (35; 37] |
| ni | 4 | 47 | 56 | 22 | 1 |
 hi = ni
Δx hi = ni
Δx
| 4/2 | 47/2 | 56/2 | 22/2 | ½ |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| Δx=2 |
| |
| hi |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
| 56⁄ 2 |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
| 47⁄ 2 |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
| 22⁄ 2 |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
| 4/2 |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
| 1/2 |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
| 27 | 29 | 31 | 33 | 35 | 37 |
|
| |
|
|
|
|
|
|
|
|
| xi |
Гистограммой относительных частот называется фигура, состоящая из прямоугольников с равными основаниями (длина интервала) и площадью численно равной относительной частоте.
|
|
|
Для построения гистограммы воспользуемся таблицей:
| xi<x≤xi+1 | (27; 29] | (29; 31] | (31; 33] | (33; 35] | (35; 37] |
| Р*i | 4/130 | 47/130 | 56/130 | 22/130 | 1/130 |
 hi = P*i
Δx hi = P*i
Δx
| 4/260 | 47/260 | 56/260 | 22/260 | 1/260 |
Δx=2
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
| h*i |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
| 56∕ 260 |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
| 47⁄ 260 |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
| 22⁄ 260 |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
| 4∕ 260 |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
| 1 ∕ 260 |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
| 0 | 27 | 29 | 31 | 33 | 35 | 37 |
|
| ||
|
|
|
|
|
|
|
|
| xi | ||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|