 |
Построение эмпирической функции распределения
|
|
|
|
Статистическая функция распределения (эмпирическая) - это частота события, состоящего в том, что случайная величина Х в процессе изменения примет значение меньше некоторого фиксированного х
F*(х) = Р* = P* (X<x)
Статистическая функция распределения (эмпирическая) является разрывной функцией, точки разрыва совпадают с наблюдаемыми значениями случайной величины, а скачок в каждой точке разрыва равен частоте появления наблюдаемого значения в данной серии наблюдения. Сумма скачков всегда равна 1.
9
Σ Pi* = 1
i=1
1) ∞ < х ≤ 28
F* (x) =P* (X<28) =0
2) 28<x≤29
F* (x) =P* (X<29) =P* (X=28) =1/130
3) 29<x≤30
F* (x) =P* (X=28) + P* (X=29) =1/130+3/130=4/130
4) 30<x≤31
F* (x) =P* (X<31) = P* (X=28) + P* (X=29) P* (X=30) +1/130+3/130+18/130=22/130
5) 31<x≤32
F* (x) =P* (X<32) = P* (X=28) + +P* (X=29) +P* (X=30) +P* (X=31) =1/130+3/130+18/130+29/130=51/130
6) 32<x≤33
F* (x) =P* (X<33) = P* (X=28) +P* (X=29) +P* (X=30) +P* (X=31)
P* (X=32) =1/130+3/130+18/130+29/130+32/130=83/130
7) 33<x≤34
F* (x) =P* (X<34) = P* (X=28) +P* (X=29) +P* (X=30) +P* (X=31) +
+P* (X=32) +P* (X=33)
=1/130+3/130+18/130+29/130+32/130+24/130=107/130
8) 34<x≤35
F* (x) =P* (X<35) = P* (X=28) +P* (X=29) +P* (X=30) +P* (X=31) +
+P* (X=32) +P* (X=33) P* (X=34) =
=1/130+3/130+18/130+29/130+32/130+24/130+18/130=125/130
9) 35<x≤36
F* (x) =P* (X<36) = P* (X=28) +P* (X=29) +P* (X=30) +P* (X=31) +
+P* (X=32) +P* (X=33) P* (X=34) + P* (X=35)
=1/130+3/130+18/130+29/130+32/130+24/130+18/130+4/130=129/130
10) x>36
F* (x) =1
0, -∞<х≤28
1/130, -∞<х≤29
4/130, 29<х≤30
22/130, 30<х≤31
F*(x) 51/130, 31<х≤32
83/130, 32<х≤33
107/130, 33<х≤34
125/130, 34<х≤35
129/130, 35<х≤36
1, х>36
Статистическая функция распределения является разрывной функцией и её графиком является ступенчатая линия.
Построим систему координат:
на оси Ох=хi
на оси Оу=F* (x)
|
Статистические оценки параметров распределения
Одной из задач статистики является оценка параметров распределения случайной величины Х по данным выборки.
Оценка параметра зависит от наблюдаемых значений и от числа наблюдений. Для того чтобы полученную оценку можно было бы использовать на практике она должна удовлетворять следующим условиям:
1) оценка должна быть не смещённой оценкой параметра, т.е. математическое ожидание должно быть равно оцениваемому параметру. Если это условие не выполняется, то оценку называют смещённой оценкой оцениваемого параметра;
2) оценка должна быть состоятельной оценкой оцениваемого параметра;
3) Оценка должна быть эффективной оценкой оцениваемого параметра;
Из всех различных оценок выбираем ту которая имеет наименьшую дисперсию она и называется эффективной если её дисперсия является минимальной из всех получившихся дисперсий.
Таким образом, чтобы полученная опытным путем оценка оцениваемого параметра была пригодной она должна быть несмещённой состоятельной и эффективной.
Пусть изучается дискретная генеральная совокупность объема N количественного признака Х.
Генеральной средней совокупностью называют среднее
 |
арифметическое наблюдаемых значений.
 |
Если же значение признака х1, х2,……. хк имеют соответственно частоты N1,N2……. Nk, то средняя генеральная вычисляется по формуле:
 |
Пусть для изучения генеральной совокупности относительно некоторого количественного признака Х произведена выборка объема n.
|
|
|
 |
Выборочной средней называют среднее арифметическое наблюдаемых значений в данной выборке.
| | ||
 | ||
Если же значение признака х1, х2,…. хk имеет соответственно частоты
 |
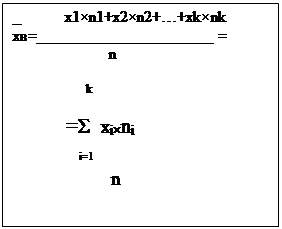n1,n2,…. nk, то выборочная средняя определяется по формуле:
 |
| xi | 28 | 29 | 30 | 32 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 18 | 29 | 32 | 24 | 18 | 4 | 1 |
28×1+29×3+30×18+31×29+32×32+33×24+34×18+35×4+36×1
хв =
130
= 4158 = 31,98
130
Выборочной дисперсией называется среднее арифметическое квадратов отклонений наблюдаемых значений от выборочной средней. Вычисляется выборочная дисперсия по формуле:
 |
Если же значение признака х1, х2…. x k имеет соответственно частоты n1,n2…. nk, то выборочная дисперсия вычисляется по формуле:
 |
(28-31,98) 2×1+ (29-31,98) 2×3+ (30-31,98) 2×18+ (31-31,98) 2×29+
Dв= + (32-31,98) 2×32+ (33-31,98) 2×24+ (34-31,98) 2×18+ (35-31,98) 2×
×4+ (36-31,98) 2×1 =
130
= 291,972 = 2,24
130
Среднее выборочное квадратичное отклонение - это величина численно равная квадратному корню из выборочной дисперсии.
 |
__
σв = √ 2,24 = 1,5
Нормальный закон распределения случайной величины
Говорят, что случайная величина распределена по нормальному закону если плотность распределения этой случайной величины выражается формулой:
 |
|
|
|
