 |
Методы обработки результатов прямых однократных измерений
|
|
|
|
В практической деятельности большинство проводимых измерений являются прямыми и однократными, в обычных условиях их точность вполне приемлема.
Прямые однократные измерения – процесс, при котором искомое значение величины находят непосредственно из опытных данных, причем сам процесс измерения выполняется только один раз.
За результат однократного измерения А принимается значение величины, полученное при измерении.
Выполнение однократных измерений обосновывают следующими факторами:
− производственной необходимостью (невозможность повторения измерения, экономическая целесообразность и т. д.);
− возможностью пренебрежения случайными погрешностями;
− случайные погрешности существенны, но доверительная граница погрешности результата измерения не превышает допускаемой погрешности измерения.
Метрологический анализ однократного измерения выявляет одно в нем следующие особенности:
1. Из множества возможных значений отсчета получается и используется только одно.
2. Представление о законе распределения вероятностей отсчета и его среднем квадратическом отклонении формируется на основе информации и опыта ранее проведенных аналогичных измерений.
При использовании этой информации уточняется:
− физическая сущность изучаемого явления;
− уточняется его модель;
− определяются факторы, влияющие на точность измерения, и меры, направленные на уменьшение влияния этих факторов (экранирование, компенсация электрических и магнитных полей и др.);
− значения поправок;
− выбор решения в пользу той или иной методики измерения;
− выбирается средство измерения, изучаются его метрологические характеристики и опыт проведения подобных измерений, проводимых ранее.
|
|
|
Итогом этой предварительной работы должна стать твердая уверенность в том, что точность однократного измерения достаточна для решения поставленной задачи.
Если это условие выполняется, то производится процесс измерения с целью получения одного значения отсчета.
Но поскольку отсчет (по основному постулату метрологи) является случайным числом, а одно единственное значение отсчета xi и получения одного единственного значения показаний Xi средства измерения, имеющего туже размерность, что и измеряемая величина, это приводит к выводу – необходимо определить погрешность, которая допущена при измерении, и провести оценивание этой погрешности.
Существует две методики оценивания погрешностей и неопределенности результата измерений, которые представлены в НТД Р 50. 038 – 2004 «Измерения прямые однократные» и подразделяются на два типа: тип А и тип В согласно требованиям РМГ 43 – 2001 (Государственная система обеспечения единства измерений. Применение «Руководства по выражению неопределенности измерений»).
Оценивание погрешности и неопределенности результата измерения по методике типа А соответствует методике выражения неопределенности измерений, принятых в основополагающих документах (НД) по метрологии, применяемых в странах – участниках Соглашения.
При оценивании погрешности и неопределенности результата измерения по методике типа В, принятой «Руководством», учитывается, что составляющими погрешности результата измерения являются погрешности СИ (средство измерения), метода измерения, оператора, а также погрешности, обусловленные изменением условий измерения. Погрешность результата однократного измерения чаще всего представлена НСП (неисключенная систематическая погрешность) и случайными погрешностями.
Характеристики НСП в этом случае могут быть представлены границами ±и и доверительными границами ±и(Р), а характеристикой случайных погрешностей могут быть – СКО S и доверительные границы ±е(Р).
|
|
|
Погрешности СИ определяют на основании их метрологических характеристик, которые указываются в нормативных и технических документах; погрешности метода измерения и оператора должны быть определены при разработке и аттестации конкретной МВИ.
Оценивание случайной погрешности и стандартной неопределенности, оцениваемой по типу А, результата измерения
Доверительные границы случайной погрешности и стандартную неопределенность результата измерения вычисляют в следующем порядке.
Если случайные погрешности представлены несколькими СКО Si 
, то СКО результата однократного измерения S(A) вычисляют по формуле:
1. Учитывая то, что погрешности представлены несколькими СКО, тогда стандартную неопределенность результата однократного измерения UA вычисляют по формуле:
Где m - число составляющих случайных погрешностей;
UiA = Si.
Доверительную границу случайной погрешности измерения е(P) вычисляют по формуле
где ZP/2 – P/2 точка нормированной функции Лапласа, отвечающая вероятности P.При доверительной вероятности P = 0,95 Z095/2 принимают равным 2, при P=0,99 Z0,99/2=2,6.
Если случайные погрешности представлены доверительными границами еi(P), соответствующими одной и той же вероятности, доверительную границу случайной погрешности результата однократного измерения вычисляют по формуле:
1.4. Если случайные погрешности представлены доверительными границами, соответствующими разным вероятностям, сначала определяют СКО измерения по формуле:
А затем вычисляют доверительные границы случайной погрешности результата измерения по формуле
Оценивание неисключенной систематической погрешности и стандартной неопределенности, оцениваемой по типу В, результата измерения.
При условии, когда неисключенная систематическая погрешность (НСП) выражена границами этой погрешности и если среди составляющих погрешности результата измерения в наличии одна НСП, то стандартную неопределенность UB, обусловленную неисключенной систематической погрешностью, заданной своими границами ± И оценивают по формуле:
|
|
|
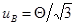
Доверительные границы НСП результата измерения вычисляют следующим образом:
1.5. Доверительную границу НСП результата измерения (без учета знака) при наличии нескольких НСП, заданных своими границами 
, доверительную границу НСП результата измерения (без учета знака) вычисляют по формуле
где k – поправочный коэффициент, определяемый принятой доверительной вероятностью и числом m составляющих
При доверительной вероятности Р =0,95 поправочный коэффициент k принимают равным 1,1.
При доверительной вероятности Р = 0,99 поправочный коэффициент k принимают равным 1,45, если число суммируемых составляющих m
Если число составляющих равно четырем (m = 4), то поправочный коэффициент k ≈ 1,4; при m = 3 k ≈ 1,3; при m = 2 k ≈ 1,2.
Суммарную стандартную неопределенность Uc,B (при условии, указанном выше в п. 1.1) вычисляют по формуле
1. 6. При наличии нескольких НСП, заданных доверительными границами рассчитанными по формуле п.1,1. доверительную границу НСП результата однократного измерения вычисляют по формуле
Суммарную стандартную неопределенность с учетом условий, указанных выше, вычисляют по формуле
где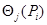 
− доверительная граница j − й НСП, соответствующая доверительной вероятности Рi;
k и ki − коэффициенты, соответствующие доверительной вероятности Р и Рi
Оценивание погрешности и расширенной неопределенности результата измерения.
1. 7. Если погрешности метода измерения и оператора пренебрежимо малы по сравнению с погрешностью используемых СИ (не превышает 15% погрешности СИ), то за погрешность результата измерения принимают погрешность используемых СИ.
1.8. Если 
то НСП или стандартной неопределенностью, оцениваемой по типу В, пренебрегают и принимают в качестве погрешности или неопределенности результата измерения доверительные границы случайной погрешности или расширенную неопределенность для уровня доверия Р, вычисляемую по формуле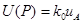 
|
|
|
Если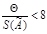 
то случайными погрешностями или стандартной неопределенностью, оцениваемой по типу А, пренебрегают и принимают в качестве погрешности или неопределенности результата измерения границы НСП или расширенную неопределенность для уровня доверия Р, вычисляемую по формуле 
1.9. Если 
то доверительную границу погрешности результата измерений ∆Р вычисляют по формуле
где К – коэффициент, значение которого для доверительной вероятности 0,95 равно 0,76; для доверительной вероятности 0,99 значение коэффициента К равно 0,83.
Расширенную неопределенность для уровня доверия Р вычисляют по формуле
где к0 коэффициент охвата (коэффициент, используемый как множитель суммарной неопределенности для получения расширенной неопределенности). Значения коэффициента охвата для доверительной вероятности Р = 0,95 считают равным 2, для доверительной вероятности Р = 0,99 − равным 3.
1.10. Форма представления результатов однократных измерений должна соответствовать МИ1317.
1.11. При симметричной доверительной погрешности результата однократного измерения представляют в форме A;± ∆(P); P или A± ∆(P), или A; U(P).
|
|
|
