 |
Метод обработки результатов прямых измерений с многократным наблюдением
|
|
|
|
Метод обработки результатов прямых измерений с многократным наблюдениями заключается в следующем. В основе любого измерения лежат прямые измерения, в ходе которых находят некоторое числовое значение физической величины. С математической точки зрения прямое измерение можно выразить уравнением, которое имеет вид:
y = cx
где y – значение исследуемой величины;
с – цена деления шкалы прибора в единицах измеряемой величины;
x – отсчет по индикаторному устройству в делениях шкалы.
Каждая измерительная операция (отсчет, замер) называется наблюдением.
Теоретически, для достижения более точных значений погрешностей измерений, необходимо провести бесконечное число наблюдений, что нереально. На практике ограничиваются конечным числом наблюдений (от единицы до нескольких десятков или сотен). Полученный при этом ряд значений физической величины x1, x2, x3…xi называют выборкой, а
R = xmax – xmin − размахом выборки.
Методы обработки результатов прямых измерений с многократными
После проведения измерений и получения результатов этих измерений необходимо:
Устранить из выборки очевидные промахи, т. е. вид грубой погрешности, зависящий от оператора и связанный с неправильным обращением со средством измерения: неверными отсчетами показаний приборов, описками при записи результатов, невнимательностью экспериментатора и т. п.
Промахи обнаруживают нестатистическими методами; и результаты наблюдений, содержащие промахи, как заведомо неправильные исключают из рассмотрения.
Исключить из результатов наблюдений систематические погрешности, являющиеся составляющими погрешности измерения и остающимися постоянной или закономерно меняющимися при повторных измерениях.
|
|
|
Упорядочить выборку в порядке возрастания ее элементов x↑I
Провести проверку выборки на наличие грубых погрешностей и ее связанность по размаху выборки
при i=1……………n-1
и проверить, содержит ли крайний элемент грубую погрешность.
Грубые погрешности крайних элементов из рассмотрения исключить.
Если выборка не является связной – эксперимент необходимо повторить.
Результат измерения и оценка его среднего квадратического отклонения.
После исключения грубых погрешностей из результатов измерений вычисляется среднеарифметическое исправленных результатов наблюдений. Эта величина принимается за результат измерения.
где n – число исправленных наблюдений.
Если во всех результатах наблюдений содержится постоянная систематическая погрешность, допускается ее исключать, но после вычисления среднего арифметического исправленных результатов измерений.
Вычисляется оценка среднего квадратического отклонения результатов измерения по формуле
Эта величина позволяет проверить, не являются ли некоторые сомнительные результаты наблюдений ошибочными.
Если окажется, что сомнительные значения отличаются от вычисленной величины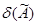 
больше, чем на три, то их следует исключить.
Вычисляется и оценивается среднее квадратическое отклонение 
результата измерения по формуле
где 
− оценка среднего квадратического отклонения результатов измерения.
Определение доверительных границ случайной погрешности результата измерения.
Доверительные границы случайной погрешности результата измерения в соответствии с требованиями ГОСТ 8. 207 – 76 устанавливают для результатов наблюдений, принадлежащих нормальному распределению.
Если это условие не выполняется, методы вычисления доверительных границ случайной погрешности должны быть указаны в методике выполнения конкретных измерений.
|
|
|
Проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению, следует проводить с уровнем значимости q от 10 о 2%. Конкретные значения уровней значимости должны быть указаны в конкретной методике выполнения измерений.
Для определения доверительных границ погрешности результата измерения доверительную вероятность Р принимают равной 0,95.
В тех случаях, когда измерение нельзя повторить, помимо границ, соответствующих доверительной вероятности Р = 0,95, допускается указывать границы для доверительной вероятности Р = 0,99.
При числе результатов наблюдений 
для проверки принадлежности их к нормальному распределению используется один из критериев 
К. Пирсона или щ2 Мизеса – Смирнова.
При числе результатов наблюдений 50 > n >16 для проверки принадлежности их к нормальному распределению предпочтительным является составной критерий.
При числе результатов наблюдений n < 50 нормальность их распределения проверяют при помощи составного критерия.
Критерий 1. Вычисляют отношение 
где 
− смещенная оценка среднего квадратического отклонения, вычисленного по формуле
Результаты наблюдений группы можно считать распределенными нормально, если
где квантели распределения, которые берутся из таблицы 1 (ГОСТ 8. 207 – 76, приложение 1) по n, 
и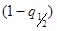 
q1 − заранее выбранный уровень значимости критерия.
Критерий 2. Можно считать, что результаты наблюдений принадлежат нормальному распределению, если не более m разностей 
превзошли значение
где S − оценка среднего квадратического отклонения, вычисляемая по формуле
где 
− верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности 
.
Значения Р определяются из таблицы 2 (ГОСТ 8. 207 – 76 приложение 1) и числу результатов наблюдений n.
При разных принимаемых уровнях значимости q для критериев 1 и 2, то уровень значимости составного критерия равен сумме частных уровней значимости.
В случае, если хотя бы один из критериев не соблюдается, то считают, что распределение результатов наблюдений группы не соответствует нормальному.
|
|
|
При числе результатов наблюдений n ≤ 15 принадлежность их к нормальному распределению не проверяют.
Доверительные границы е (без учета знака) случайной погрешности результата измерения находят по формуле
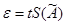
где t − коэффициент Стьюдента, который в зависимости от доверительной вероятности Р и числа наблюдений n находят по таблице справочного приложения 2 ГОСТ 8. 207 – 76.
Определение доверительных границ неисключенной систематической погрешности результата измерения.
Неисключенная систематическая погрешность результата образуется из составляющих, в качестве корторых могут быть неисключенные систематические погрешности: метода измерения; средства измерения; вызванные другими источниками.
В качестве границ составляющих неисключенной систематической погрешности принимают пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежительно малы.
При суммировании составляющих неисключенной систематической погрешности результата измерения неисключенные систематические погрешности средств измерения каждого типа и погрешности поправок рассматривают как случайные величины. При отсутствии данных о виде распределения случайных величин их распределение принимают за равномерное.
Границы неисключенной систематической погрешности И результата измерения вычисляют путем построения композиции неисключенных систематических погрешностей средств измерений, метода и погрешностей, вызванных другими источниками. При равномерном распределении неисключенных систематических погрешностей эти границы (без учета знака) можно вычислить по формуле
где Иi − граница i – й неисключенной систематической погрешности;
k − коэффициент, определяемый принятой доверительной вероятностью. Коэффициент k принимают равным 1,1 при доверительной вероятности Р = 0,95.
Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что при вычислении доверительных границ случайной погрешности результата измерения.
|
|
|
Определение границ погрешности результата измерения.
В случае 
, то неисключенными систематическими погрешностями по сравнению со случайными пренебрегают и принимают, что граница погрешности результата ∆=е. Если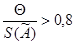 
, то случайной погрешностью по сравнению с систематическими пренебрегают и принимают, что граница погрешности результата ∆=И.
В случае, если неравенства, указанные в п. 2.7.1. не выполняются, границу погрешности результата измерения находят путем построения композиции распределения случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины в соответствии с
Если доверительные границы случайных погрешностей найдены в соответствии с п. 2.4. допускается границы погрешности результата измерения ∆ (без учета знака) вычислять по формуле
где К − коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;
SУ − оценка суммарного среднего квадратического отклонения результата измерения.
Оценку суммарного среднего квадратического отклонения результата измерения вычисляют по формуле
Коэффициент К вычисляют по эмпирической формуле
Форма записи результатов измерений.
Оформление результатов измерений производится в соответствии с МИ 1317 – 2001.
При симметричной доверительной погрешности результаты измерений представляют в форме
где 
− результат измерения.
Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности ∆.
При отсутствии данных о виде функций распределений составляющих погрешности результата и необходимости дальнейшей обработки результатов или анализа погрешностей, результаты измерений представляют в форме
|
|
|
