 |
Криволинейный интеграл первого рода
|
|
|
|
Кратные и криволинейные интегралы
До сих пор в настоящем курсе интегрирование проводилось по заданному отрезку (интеграл Римана) или интервалу (несобственные интегралы) оси  . С помощью замены переменной можно было осуществлять интегрирование по отрезку другой плоской прямой. Но только вдоль прямой.
. С помощью замены переменной можно было осуществлять интегрирование по отрезку другой плоской прямой. Но только вдоль прямой.
Однако с помощью этих интегралов невозможно получить решение многих задач. Это задача определения, объема, массы тел, если эти тела недоступны или трудно доступны (например, массы планет солнечной системы), вычисление работы некоторой силы на криволинейном участке пути. Невозможно интегрирование по части пространственной прямой или кривой.
Для этой цели вводятся интегралы более общего вида – криволинейные, двойные, тройные, поверхностные.
Криволинейный интеграл первого рода
Пусть требуется решить задачу определения массы тела, один размер которого значительно больше остальных (массивная цепь, например).
Очевидно, при составлении математической модели это тело можно считать массивной линией, то есть линией, обладающей массой. Введем понятие плотности линии - массу ее элемента единичной длины. Если плотность линии меняется от точки к точке, то это функция двух переменных, если линия плоская, или трех переменных для пространственной линии. Линия может быть прямой, тогда ее масса определяется интегралом Римана. Решение задачи для кривых приводит к криволинейному интегралу первого рода.
Рассмотрим массивную плоскую кривую, ограниченную точками  и
и 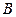 , ее плотность
, ее плотность  . Разобьем кривую на
. Разобьем кривую на  элементарных частей длина каждого элемента
элементарных частей длина каждого элемента  . Пусть
. Пусть  достаточно большое, чтобы можно было плотность приближенно считать постоянной на каждом ее элементарном ее отрезке. Выберем на каждом элементарном отрезке точку
достаточно большое, чтобы можно было плотность приближенно считать постоянной на каждом ее элементарном ее отрезке. Выберем на каждом элементарном отрезке точку 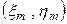 . Тогда
. Тогда
|
|
|
 приближенное значение массы этой кривой. Увеличиваем число разбиений, причем так, чтобы длина каждого элементарного отрезка
приближенное значение массы этой кривой. Увеличиваем число разбиений, причем так, чтобы длина каждого элементарного отрезка  уменьшалась, стремясь к нулю при
уменьшалась, стремясь к нулю при 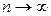 .
.
Очевидно,  является обобщением интегральной суммы Римана, тогда ее предел
является обобщением интегральной суммы Римана, тогда ее предел  , с одной стороны, равен точному значению массы кривой, с другой стороны, может считаться по аналогии с интегралом Римана интегралом по кривой, или криволинейным интегралом (первого рода). Итак, масса тела
, с одной стороны, равен точному значению массы кривой, с другой стороны, может считаться по аналогии с интегралом Римана интегралом по кривой, или криволинейным интегралом (первого рода). Итак, масса тела 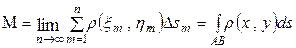 .
.
Отметим, что вопрос существования предела интегральной суммы Римана, а, следовательно, криволинейного интеграла в данном случае не стоит, поскольку задача реальная, масса тела существует.
Отвлечемся от реалий, поставим задачу абстрактно.
Определение. Криволинейным интегралом первого рода от функции 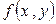 по кривой
по кривой 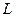 называется предел интегральной суммы
называется предел интегральной суммы  , если он существует и не зависит от способа разбиения кривой
, если он существует и не зависит от способа разбиения кривой 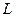 и выбора точек
и выбора точек 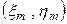 .
.
Примечание. Криволинейный интеграл  не зависит от направления интегрирования, то есть от того, интегрирование ведется от точки
не зависит от направления интегрирования, то есть от того, интегрирование ведется от точки  к
к 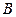 или от
или от 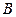 к
к  . Это следует из определения, поскольку
. Это следует из определения, поскольку  - длина элементарного отрезка, то есть положительная величина.
- длина элементарного отрезка, то есть положительная величина.
Как будет установлено ниже, это единственное свойство криволинейного интеграла первого рода, отличное от свойств определенного интеграла.
Вычисление криволинейного интеграла первого рода
I. Вычислить  , если уравнение кривой задано в явном виде
, если уравнение кривой задано в явном виде 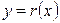 .
.
Чтобы вычислить новый интеграл, необходимо свести его какому то известному. Ясно, что ближе всего к нему определенный интеграл.
Пусть точка  кривой имеет координаты
кривой имеет координаты  , точка
, точка 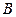 соответственно
соответственно  , причем
, причем  . Тогда
. Тогда
 ,
,
здесь  длина дуги элементарного отрезка кривой.
длина дуги элементарного отрезка кривой.
В силу малости длин этих дуг заменяем их хордами, фактически вычисляя интеграл по ломаной линии. Тогда  , где
, где 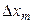 и
и  проекции элементарной хорды на оси координат. В этом случае
проекции элементарной хорды на оси координат. В этом случае
|
|
|
 .
.
Поскольку  , правая часть вышеприведенной формулы представляет собой предел интегральной суммы Римана для функции одной переменной, то есть определенный интеграл. Итак,
, правая часть вышеприведенной формулы представляет собой предел интегральной суммы Римана для функции одной переменной, то есть определенный интеграл. Итак,
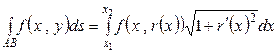 .
.
Криволинейный интеграл первого рода приведен к определенному интегралу. Но этот последний зависит от направления интегрирования. Противоречие снимается, если в полученной формуле нижний предел интегрирования определенного интеграла меньше верхнего, то есть интегрирование идет от меньших чисел к большим, и все 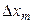 положительны. За этим нужно обязательно следить.
положительны. За этим нужно обязательно следить.
Примечания. 1. Поскольку криволинейный интеграл приведен к интегралу Римана, все его свойства, кроме упомянутого в предыдущем примечании, совпадают со свойствами определенного интеграла.
2. Криволинейный интеграл первого рода существует, если подынтегральная функция непрерывна в точках кривой, сама кривая гладкая, производная уравнения кривой также непрерывна. При этих условиях существует интеграл Римана в вышеприведенной формуле, следовательно, и криволинейный интеграл.
Пример. Вычислить  , где
, где 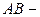 дуга параболы
дуга параболы  , заключенная между точками
, заключенная между точками  и
и 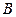 с абсциссами 1 и 3 соответственно.
с абсциссами 1 и 3 соответственно.
Поскольку  , получаем
, получаем

 .
.
Вычислим этот же интеграл с помощью МАКСИМЫ

Первой командой задается уравнение кривой, по которой происходит интегрирование, вторая команда формирует подынтегральную функцию, третья упрощает ее вид с помощью тождественных преобразований, четвертая вычисляет интеграл.
II. Вычислить  , если уравнение кривой задано в параметрическом виде
, если уравнение кривой задано в параметрическом виде  , причем точке
, причем точке  соответствует значение параметра
соответствует значение параметра  , точке
, точке  соответственно
соответственно  .
.
В этом случае  , следовательно,
, следовательно,

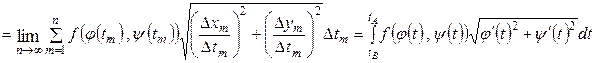 .
.
Итак,
 .
.
Пример. Вычислить 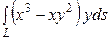 , где
, где 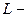 длина дуги окружности
длина дуги окружности 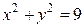 , заключенной между точками, полярные углы которых
, заключенной между точками, полярные углы которых  и
и  .
.
Запишем уравнение окружности в параметрическом виде 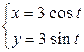 , тогда параметр
, тогда параметр  меняется от
меняется от  до
до  .
.
Поскольку  ,
,  , тогда
, тогда

С помощью МАКСИМЫ

III. Вычислить  , если уравнение кривой задано в параметрическом виде, причем точке
, если уравнение кривой задано в параметрическом виде, причем точке  соответствует значение параметра
соответствует значение параметра  , точке
, точке  соответственно
соответственно  .
.
Обобщая полученную в пункте II формулу, имеем
 .
.
Пример. Вычислить  по прямой
по прямой  , если
, если
 ,
,  . Запишем уравнение прямой в параметрическом виде
. Запишем уравнение прямой в параметрическом виде
|
|
|
 . Очевидно,
. Очевидно,  . Тогда
. Тогда  .
.
Точке  соответствует
соответствует  , для точки
, для точки 
 .
.



 .
.
С помощью МАКСИМЫ

|
|
|


