 |
Криволинейный интеграл второго рода
|
|
|
|
Выберем декартову систему координат, совместим с ней ортонормированный базис 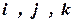 .
.
Вычислим работу некоторой силы 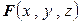 на криволинейном участке пути
на криволинейном участке пути  . Разобьем кривую
. Разобьем кривую  на
на  элементарных частей и соединим соседние точки кривой прямыми, получившиеся при этом хорды образуют ломаную линию, которая при
элементарных частей и соединим соседние точки кривой прямыми, получившиеся при этом хорды образуют ломаную линию, которая при  достаточно большом мало отличается от кривой
достаточно большом мало отличается от кривой  .
.
С учетом направления прохождения ломаной каждая элементарная хорда представляет собой вектор, обозначим его 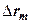 . Если
. Если  достаточно большое, можно приближенно считать, что сила не меняется в пределах элементарного участка. Выберем на каждом элементе точку
достаточно большое, можно приближенно считать, что сила не меняется в пределах элементарного участка. Выберем на каждом элементе точку  и подсчитаем в ней значение силы
и подсчитаем в ней значение силы  . Работа силы на участке
. Работа силы на участке 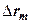 , как известно, определяется скалярным произведением этих векторов. В ортонормированном базисе
, как известно, определяется скалярным произведением этих векторов. В ортонормированном базисе 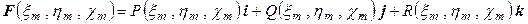 ,
,
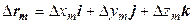 . Тогда работа на элементарном участке примет вид
. Тогда работа на элементарном участке примет вид
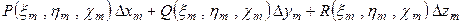 ,
,
Работа силы на всей ломаной равна
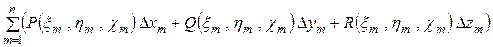 ,
,
то есть сумме, напоминающей интегральную сумму Римана.
Увеличиваем число разбиений, причем так, чтобы длина каждого элементарного отрезка уменьшалась, стремясь при 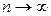 к нулю. При этом условии ломаная практически не отличается от кривой
к нулю. При этом условии ломаная практически не отличается от кривой  , истинное значение работы, совершаемое силой при прохождении кривой
, истинное значение работы, совершаемое силой при прохождении кривой 
 .
.
Поскольку работа, совершаемая силой при прохождении кривой конкретна, этот предел существует и имеет конечное значение. По аналогии считаем этот предел интегралом

 .
.
Этот криволинейный интеграл второго рода дает истинное значение работы.
Отвлечемся от реального смысла задачи. В этом случае предел интегральной суммы существует не всегда. Отсюда получаем
Определение. Криволинейным интегралом второго рода  называется предел интегральной суммы
называется предел интегральной суммы  , если он существует и не зависит от способа разбиения кривой
, если он существует и не зависит от способа разбиения кривой  и выбора точек
и выбора точек  .
.
|
|
|
Вычисление криволинейного интеграла второго рода
I. Пусть кривая 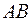 задана параметрически
задана параметрически  , точке
, точке 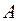 соответствует значение параметра
соответствует значение параметра  , для точки
, для точки 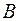 параметр
параметр 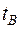 .
.
По определению 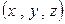 - координаты точки кривой
- координаты точки кривой 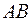 , то есть удовлетворяют уравнению, тогда
, то есть удовлетворяют уравнению, тогда  , и в соответствии с формулой, определяющей интеграл, имеем
, и в соответствии с формулой, определяющей интеграл, имеем

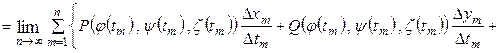
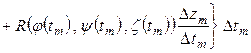 .
.
Интегральная сумма в правой части не отличается от интегральной суммы Римана для функции одной переменной  . Таким образом, вычисление криволинейного интеграла второго рода производится по формуле
. Таким образом, вычисление криволинейного интеграла второго рода производится по формуле

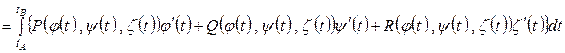 .
.
Примечание. 1. Из полученной формулы следует, что все свойства определенного интеграла совпадают со свойствами криволинейного интеграла второго рода, в том числе
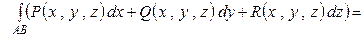
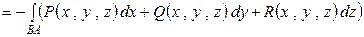 .
.
При вычислении криволинейного интеграла второго рода пределы интегрирования в определенном интеграле, следовательно, расставляются так – нижний предел соответствует начальной точке кривой, верхний – ее конечной точке.
II. Параметрическое уравнение плоской кривой  имеет вид
имеет вид  , следовательно,
, следовательно,
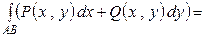
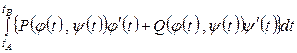 .
.
III. При явном задании кривой 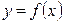 поступаем следующим образом. В качестве параметра принимаем переменную
поступаем следующим образом. В качестве параметра принимаем переменную 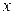 , что позволяет использовать уравнение кривой в виде
, что позволяет использовать уравнение кривой в виде 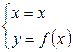 , тогда
, тогда 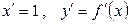 , и формула перехода от криволинейного интеграла второго рода к определенному интегралу запишется следующим образом
, и формула перехода от криволинейного интеграла второго рода к определенному интегралу запишется следующим образом
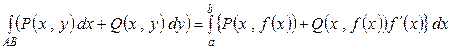 .
.
Примеры. Вычислить
1. 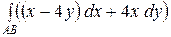 , где
, где  - четверть окружности
- четверть окружности 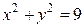 , расположенная в первой четверти. Запишем параметрическое уравнение этой окружности
, расположенная в первой четверти. Запишем параметрическое уравнение этой окружности 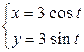 . Нетрудно заметить, что при прохождении этой части окружности от точки
. Нетрудно заметить, что при прохождении этой части окружности от точки  , лежащей на оси абсцисс, до точки
, лежащей на оси абсцисс, до точки 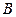 на оси ординат параметр
на оси ординат параметр  меняется от 0 до
меняется от 0 до  .
.
Поскольку  , получаем
, получаем
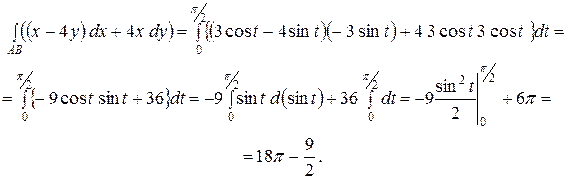
С помощью МАКСИМЫ

2.  по дуге параболы
по дуге параболы 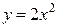 от точки
от точки 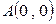 до
до 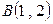
Поскольку  , имеем
, имеем
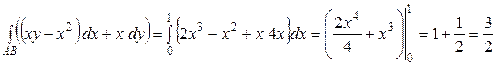 .
.

Теорема. Условием необходимым и достаточным независимости криволинейного интеграла второго рода  от пути интегрирования является равенство нулю интеграла по любому замкнутому контуру, содержащему точки
от пути интегрирования является равенство нулю интеграла по любому замкнутому контуру, содержащему точки  и
и 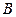 .
.
|
|
|
Необходимость. Изобразим замкнутую кривую 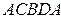 , не налагая на нее никаких ограничений, кроме того, что точки
, не налагая на нее никаких ограничений, кроме того, что точки  и
и 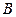 лежат на этой кривой. Пусть
лежат на этой кривой. Пусть  , то есть он не зависит от пути интегрирования. Переносим интеграл из правой части в левую
, то есть он не зависит от пути интегрирования. Переносим интеграл из правой части в левую
 .
.
Используя свойства криволинейного интеграла второго рода, полностью совпадающие со свойствами определенного интеграла, получаем
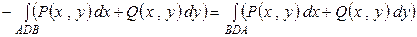 .
.
Но
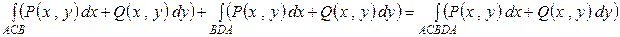
Таким образом, 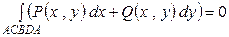 . Необходимость доказана.
. Необходимость доказана.
Достаточность. Имеем 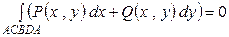 , очевидно,
, очевидно,
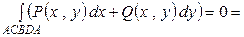
 ,
,
откуда следует
 Теорема доказана.
Теорема доказана.
Примеры для самостоятельного решения
Вычислить интегралы
18.1. 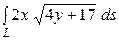 ,
, 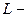 дуга параболы
дуга параболы  , заключенная между точками
, заключенная между точками  до
до 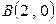 .
.
18.2.  по дуге эллипса
по дуге эллипса 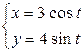 , расположенной в первой четверти.
, расположенной в первой четверти.
18.3. 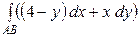 , где
, где 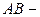 арка циклоиды
арка циклоиды  .
.
18.4. 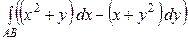 ,
, 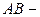 прямая, соединяющая точки
прямая, соединяющая точки 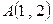 и
и  .
.
Двойной интеграл
Рассмотрим практически важную задачу определения объема тела, недоступного для исследователя, когда становится невозможным традиционное определение объема с помощью вытесняемой этим телом жидкости.
Объем тела
Задано тело, ограниченное снизу частью плоскости 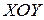 , сверху гладкой поверхностью
, сверху гладкой поверхностью 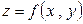 и некоторой цилиндрической боковой поверхностью. Простейшим примером этой задачи является определение объема снега, набитого в цилиндрическую бочку "с шапкой".
и некоторой цилиндрической боковой поверхностью. Простейшим примером этой задачи является определение объема снега, набитого в цилиндрическую бочку "с шапкой".
Пусть проекция этого тела на плоскость 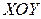 представляет собой область
представляет собой область  , причем имеет не равную нулю площадь, то есть не является линией или точкой.
, причем имеет не равную нулю площадь, то есть не является линией или точкой.
Разобьем область  на
на  произвольных элементарных подобластей, площадь каждой из них
произвольных элементарных подобластей, площадь каждой из них 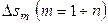 . Выберем внутри каждой подобласти точку
. Выберем внутри каждой подобласти точку 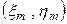 и восстановим из этих точек перпендикуляры до пересечения с поверхностью
и восстановим из этих точек перпендикуляры до пересечения с поверхностью 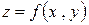 , очевидно,
, очевидно, 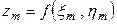 . Построим элементарные цилиндры, площадь основания каждого из них
. Построим элементарные цилиндры, площадь основания каждого из них  , высота
, высота  . Вычислим суммарный объем всех этих цилиндров
. Вычислим суммарный объем всех этих цилиндров
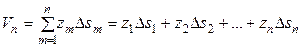
или
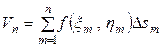 .
.
Очевидно, 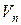 дает приближенное значение объема заданного тела. Если увеличивать число площадок разбиения
дает приближенное значение объема заданного тела. Если увеличивать число площадок разбиения  , следя за тем, чтобы площадь каждой элементарной площадки уменьшалась, то при очень больших значениях
, следя за тем, чтобы площадь каждой элементарной площадки уменьшалась, то при очень больших значениях  приближенное значение объема тела будет мало отличаться от объема тела.
приближенное значение объема тела будет мало отличаться от объема тела.
Истинное значение объема тела может быть подсчитано с помощью формулы
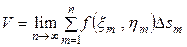 .
.
Так как функция под знаком предела представляет собой вариант интегральной суммы Римана, можно ввести интеграл, равный пределу этой интегральной суммы
|
|
|

или
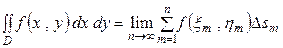 .
.
Такой интеграл называют двойным интегралом, поскольку интегрирование проводится по двумерной области 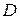 , называемой областью интегрирования, а, следовательно, по двум переменным
, называемой областью интегрирования, а, следовательно, по двум переменным 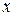 и
и 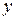 .
.
Поскольку объем реального тела конечен, предел интегральной суммы существует и имеет конечное значение, существует и двойной интеграл.
Если ставить задачу абстрактно, не связываясь с реальностью, предел интегральной суммы, а значит и двойной интеграл может не существовать.
При установлении необходимого и достаточного условий существования двойного интеграла приходится столкнуться с проблемой, решаемой ранее при изучении интеграла Римана. Не вдаваясь в тонкости этого исследования, примем без доказательства, что для существования двойного интеграла достаточно, чтобы подынтегральная функция 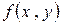 была непрерывной в замкнутой области интегрирования
была непрерывной в замкнутой области интегрирования 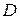 .
.
Основные свойства двойного интеграла
1.  для
для 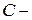 постоянной.
постоянной.
Доказательство.
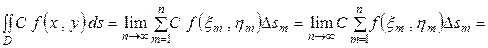
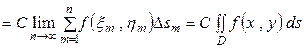 .
.
2. 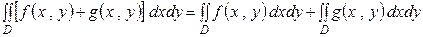
Доказательство.
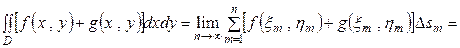
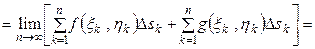

 .
.
3.  , если
, если 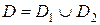 (без доказательства).
(без доказательства).
Вычисление двойного интеграла
Вычисление двойного интеграла осуществляется сведением его к повторному интегралу, то есть к вычислению определенного интеграла сначала по одной переменной, затем по другой. Такое сведение производится при помощью следующей леммы.
Лемма. Объем тела может быть вычислен по формуле 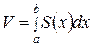 , где
, где  площадь сечения тела плоскостью
площадь сечения тела плоскостью  const.,
const., 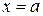 и
и  - плоскости, ограничивающие заданное тело.
- плоскости, ограничивающие заданное тело.
Доказательство.
Разобьем область, занимаемую телом, плоскостями 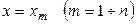 на
на  элементарных подобластей и заменим эти элементарные тела цилиндрами, причем площадь основания каждого цилиндра совпадает с площадью сечения
элементарных подобластей и заменим эти элементарные тела цилиндрами, причем площадь основания каждого цилиндра совпадает с площадью сечения  тела соответствующей плоскостью, высота
тела соответствующей плоскостью, высота  . Суммарный объем этих цилиндров
. Суммарный объем этих цилиндров 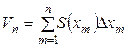 , с одной стороны, дает приближенное значение объема рассматриваемого тела, с другой стороны, представляет интегральную сумму Римана.
, с одной стороны, дает приближенное значение объема рассматриваемого тела, с другой стороны, представляет интегральную сумму Римана.
Увеличивая число разбиений области  , следя за тем, чтобы все
, следя за тем, чтобы все 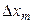 при этом уменьшались, определяем объем заданного тела все более точно. Наконец, переходя к пределу
при этом уменьшались, определяем объем заданного тела все более точно. Наконец, переходя к пределу 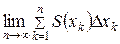 , получаем точное значение объема тела. Но, как известно, предел интегральной суммы Римана, если он существует и не зависит от способа разбиения области, является определенным интегралом. Следовательно,
, получаем точное значение объема тела. Но, как известно, предел интегральной суммы Римана, если он существует и не зависит от способа разбиения области, является определенным интегралом. Следовательно, 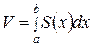 , что требовалось доказать.
, что требовалось доказать.
|
|
|
I. Вычислим объем тела, ограниченного плоскостями 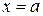 ,
,  ,
, 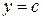 ,
, 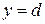 ,
, 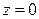 и поверхностью
и поверхностью  , то есть призмы с "крышкой". Для этого воспользуемся формулой
, то есть призмы с "крышкой". Для этого воспользуемся формулой 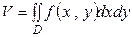 , причем область
, причем область 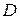 , представляет собой проекцию призмы на плоскость
, представляет собой проекцию призмы на плоскость 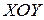 , то есть прямоугольник, изображенный на рисунке 54
, то есть прямоугольник, изображенный на рисунке 54
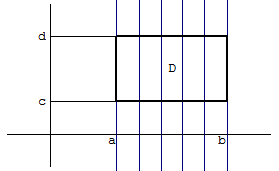
Рисунок 54.
Чтобы воспользоваться формулой 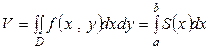 , рассекаем тело плоскостями
, рассекаем тело плоскостями 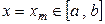 . Каждое сечение представляет собой трапецию, основанием которой является отрезок вертикальной прямой в области
. Каждое сечение представляет собой трапецию, основанием которой является отрезок вертикальной прямой в области 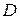 , изображенной на рисунке 54. Из рисунка следует, что длины оснований всех трапеций одинаковы, так как расположены между параллельными прямыми
, изображенной на рисунке 54. Из рисунка следует, что длины оснований всех трапеций одинаковы, так как расположены между параллельными прямыми  и
и 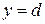 . Трапеция в сечении
. Трапеция в сечении 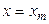 ограничена сверху линией
ограничена сверху линией  . Площадь каждой трапеции равна
. Площадь каждой трапеции равна  , что следует из геометрического смысла определенного интеграла. Тогда в соответствии с леммой
, что следует из геометрического смысла определенного интеграла. Тогда в соответствии с леммой
 .
.
Таким образом, двойной интеграл сводится к повторному, то есть к двум определенным интегралам
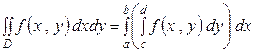 ,
,
при этом сначала вычисляется внутренний интеграл (по 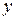 ) затем внешний интеграл (по
) затем внешний интеграл (по 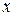 ).
).
II. Вычисление интеграла  по более сложной, чем прямоугольник, области
по более сложной, чем прямоугольник, области 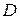 . Пусть области
. Пусть области 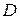 - часть плоскости
- часть плоскости 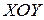 , ограниченная линиями
, ограниченная линиями 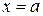 ,
,  ,
, 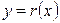 ,
, 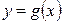 и изображенная на рисунке 55
и изображенная на рисунке 55
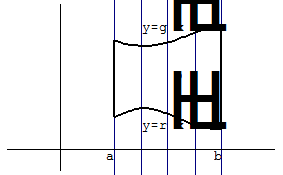
Рисунок 55.
В этом случае тело, объем которого равен вычисляемому интегралу, представляет собой цилиндр, ограниченный снизу плоскостью 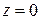 , сверху поверхностью
, сверху поверхностью  . Направляющей цилиндра является замкнутый контур, ограничивающий область
. Направляющей цилиндра является замкнутый контур, ограничивающий область 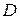 .
.
Рассекаем тело плоскостями 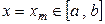 . В каждом сечении получаем трапеции, их основаниями являются отрезки вертикальных прямых, изображенных на рисунке 55. В отличие от предыдущего случая, основания этих трапеций уже не равны и, как это видно из рисунка, находятся между точками
. В каждом сечении получаем трапеции, их основаниями являются отрезки вертикальных прямых, изображенных на рисунке 55. В отличие от предыдущего случая, основания этих трапеций уже не равны и, как это видно из рисунка, находятся между точками 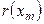 ,
, 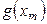 . Тогда площадь трапеции в плоскости
. Тогда площадь трапеции в плоскости 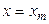 вычисляется с помощью определенного интеграла
вычисляется с помощью определенного интеграла 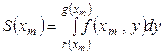 . В соответствии с леммой получаем
. В соответствии с леммой получаем
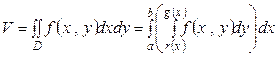 .
.
Двойной интеграл опять сводится к повторному, то есть к двум определенным интегралам, однако, пределы внутреннего интеграла зависят от 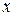 .
.
Замечание. Результат не зависит от того, по какой переменной осуществляется внутреннее и внешнее интегрирование, то есть
 .
.
Как уже говорилось выше, линии 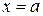 ,
,  ограничивают область
ограничивают область 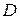 слева и справа, линии
слева и справа, линии 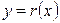 ,
, 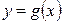 ограничивают ее снизу и сверху. Линии
ограничивают ее снизу и сверху. Линии  ,
, 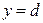 ограничивают область интегрирования снизу и сверху,
ограничивают область интегрирования снизу и сверху, 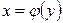 и
и  - уравнения линий, ограничивающих ее слева и справа.
- уравнения линий, ограничивающих ее слева и справа.
|
|
|
Пример 1.
Вычислить 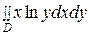 , область
, область 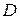 ограничена линиями
ограничена линиями 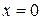 ,
,  ,
, 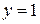 ,
, 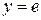 . Таким образом, область интегрирования представляет прямоугольник, следовательно, имеет место случай I. Тогда
. Таким образом, область интегрирования представляет прямоугольник, следовательно, имеет место случай I. Тогда
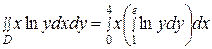 .
.
Вычислим по частям внутренний интеграл
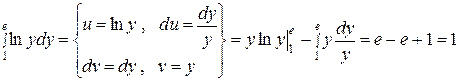 ,
,
Вычисляем внешний интеграл 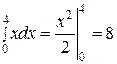 . Итак,
. Итак, 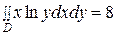 .
.
С помощью МАКСИМЫ

Пример 2.
Вычислить 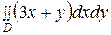 по области, задаваемой неравенствами
по области, задаваемой неравенствами 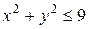 и
и  . Область интегрирования – верхняя из двух получаемых в этом случае областей (рисунок 56)
. Область интегрирования – верхняя из двух получаемых в этом случае областей (рисунок 56)
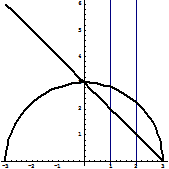
Рисунок 56.
Сечения  const. показывают, что вход в область интегрирования осуществляется через прямую
const. показывают, что вход в область интегрирования осуществляется через прямую  , выход из области происходит через верхнюю полуокружность
, выход из области происходит через верхнюю полуокружность 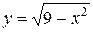 . Тогда
. Тогда
 .
.
Вычисляем внутренний интеграл

 .
.
Теперь вычисляется внешний интеграл

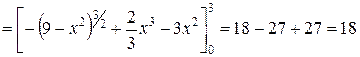 .
.
Таким образом, 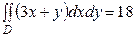 .
.
Пример 3. Вычислить 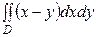 , если область
, если область 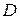 ограничена линиями
ограничена линиями 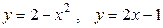 . Рассмотрим два способа вычисления интеграла.
. Рассмотрим два способа вычисления интеграла.
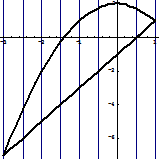
1 способ. Пусть внешнее интегрирование по 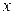 , внутреннее – по
, внутреннее – по 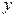 . Штрихуем область интегрирования вертикальными прямыми
. Штрихуем область интегрирования вертикальными прямыми  const. (рисунок 57 a). Нетрудно заметить, что если идти от меньших значений
const. (рисунок 57 a). Нетрудно заметить, что если идти от меньших значений 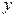 к большим, точки входа в область интегрирования лежат на прямой
к большим, точки входа в область интегрирования лежат на прямой 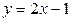 , точки выхода расположены на параболе
, точки выхода расположены на параболе  .
.
а) в)
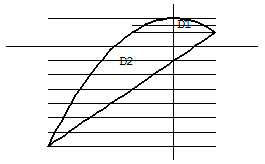
Рисунок 57.
Очевидно,
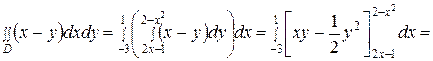
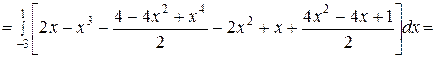
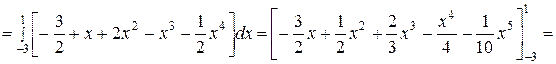
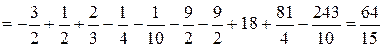 .
.

2 способ. Пусть внешнее интегрирование по 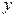 , внутреннее – по
, внутреннее – по 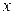 . В этом случае штрихуем область
. В этом случае штрихуем область  прямыми
прямыми 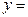 const. (рисунок 57 в) и проходить ее нужно слева направо. Из рисунка следует, что область интегрирования разбивается на две
const. (рисунок 57 в) и проходить ее нужно слева направо. Из рисунка следует, что область интегрирования разбивается на две  и
и 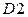 . Область
. Область  находится между прямыми
находится между прямыми 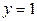 и
и 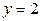 , область
, область 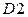 - между прямыми
- между прямыми  и
и 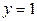 . Тогда
. Тогда
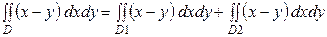 =
=
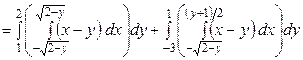 .
.
Вычислим интегралы
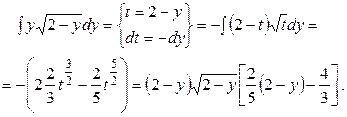
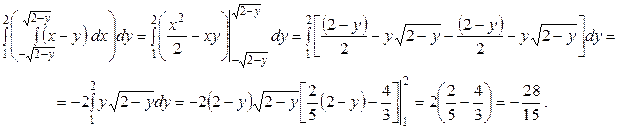
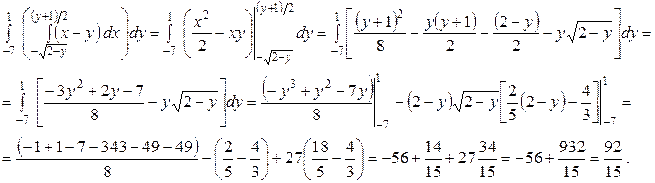 Ответ
Ответ 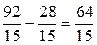 .
.
Оба способа дали, естественно, один ответ, однако второй способ привел к необходимости разбивать область интегрирования на две, что усложнило вычисление интеграла.
Формула Грина
Установим связь между криволинейным интегралом второго рода и двойным интегралом. Докажем так называемую формулу Грина
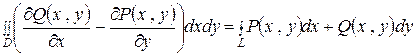 .
.
Здесь  область интегрирования двойного интеграла,
область интегрирования двойного интеграла,  замкнутый контур, ограничивающий область
замкнутый контур, ограничивающий область 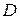 (рисунок 58).
(рисунок 58).

Рисунок 58.
его верхняя часть имеет уравнение 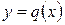 , уравнение его нижней части
, уравнение его нижней части 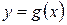 . С учетом этого область
. С учетом этого область 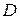 можно изобразить следующим образом (рисунок 59)
можно изобразить следующим образом (рисунок 59)
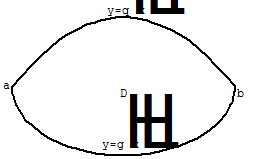
Рисунок 59.
Рассмотрим интеграл
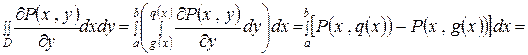
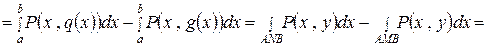
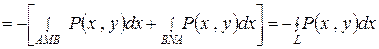 .
.
При выведении этой формулы сначала двойной интеграл сводится к повторному, затем проводится внутреннее интегрирование по 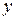 , после чего получаются два интеграла Римана, которые сводятся к двум криволинейным интегралам второго рода, что в конечном итоге дает криволинейный интеграл по замкнутому контуру
, после чего получаются два интеграла Римана, которые сводятся к двум криволинейным интегралам второго рода, что в конечном итоге дает криволинейный интеграл по замкнутому контуру 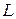 .
.
Для доказательства второй части формулы Грина рисунок 58 заменим рисунком 60,

Рисунок 60.
причем область изменения 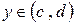 , кроме того, уравнение левой стороны контура
, кроме того, уравнение левой стороны контура 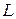 задается уравнением
задается уравнением 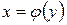 , правой его части
, правой его части 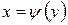 . Тогда
. Тогда

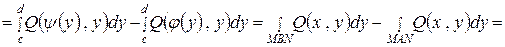
 .
.
При проведении этих преобразований используется описанная выше процедура приведения двойного интеграла к криволинейному, отличие в том, что вначале проводится интегрирование по 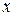 , затем по
, затем по 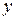 .
.
Объединяя обе формулы, приходим к формуле Грина
 .
.
Примечание. При рассмотрении криволинейных интегралов второго рода было установлено, что он не зависит от пути интегрирования, если интеграл по любому замкнутому контуру, содержащему начальную и конечную точки интегрирования, равен нулю. Применение формулы Грина позволяет дать более удобную для применения формулировку этой теоремы.
Теорема. Условием, необходимым и достаточным независимости криволинейного интеграла второго рода  от пути интегрирования, является
от пути интегрирования, является 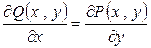 .
.
Доказательство. Ранее было доказано, что интеграл по любому замкнутому контуру, содержащему точки  и
и 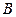 в этом случае равен нулю. Следовательно, в формуле Грина правый интеграл равен нулю, значит, равен нулю и левый интеграл, что возможно лишь при
в этом случае равен нулю. Следовательно, в формуле Грина правый интеграл равен нулю, значит, равен нулю и левый интеграл, что возможно лишь при 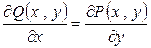 .
.
Пример.
Вычислить интеграл 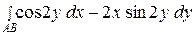 , если
, если  ,
,  .
.
Очевидно, 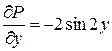 ,
, 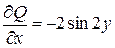 , то есть выполняется условие независимости интеграла от пути интегрирования. Вычислим интеграл по ломаной
, то есть выполняется условие независимости интеграла от пути интегрирования. Вычислим интеграл по ломаной  , изображенной на рисунке 61
, изображенной на рисунке 61
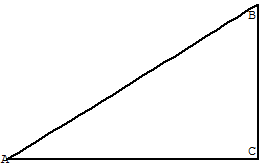
Рисунок 61.
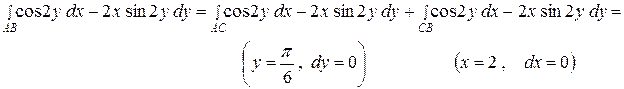
 .
.
Замена переменной в двойном интеграле
Традиционный вывод перехода в двойном интеграле от старых переменных к новым достаточно громоздок и труден для восприятия. Предлагается проделать этот путь с помощью формулы Грина.
Пусть в интеграле  требуется перейти к переменным
требуется перейти к переменным
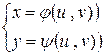
Используем формулу Грина, считая 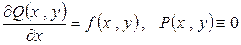 :
:
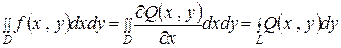 .
.
Проведем в контурном интеграле упомянутую замену переменных
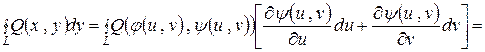
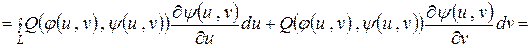
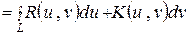 ,
,
где
 .
.
Применяя еще раз формулу Грина, возвращаемся к двойному интегралу, но уже относительно новых переменных
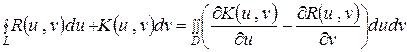 .
.
Остается вычислить вошедшие в интеграл производные
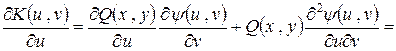
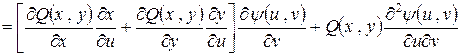 ,
,
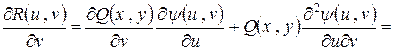
 .
.
Теперь вычислим

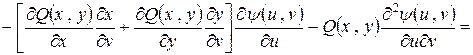
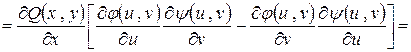
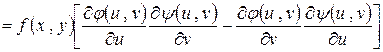 .
.
Обозначим
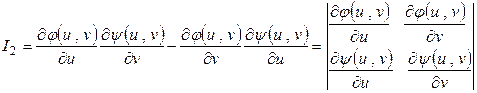
и назовем это выражение Якобианом преобразования, после чего приходим к формуле, определяющей замену переменных
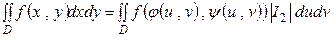 .
.
Таким образом, при замене переменных в двойном интеграле в отличие от замены переменных в уже известных интегралах появляется Якобиан преобразования
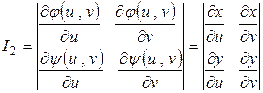 .
.
Переход от декартовой системы координат к полярной
Поскольку нам известны только две системы координат на плоскости – декартова и полярная, связанные соотношениями 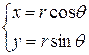 , осуществим в двойном интеграле переход от одной системы координат к другой.
, осуществим в двойном интеграле переход от одной системы координат к другой.
Очевидно, якобиан преобразования в этом случае имеет вид
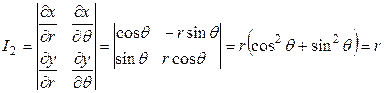 .
.
В результате
 .
.
Пример 1.
Вычислить интеграл  по кольцу, ограниченному окружностями
по кольцу, ограниченному окружностями 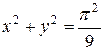 и
и  . Используем формулы перехода от декартовых координат к полярным
. Используем формулы перехода от декартовых координат к полярным 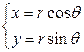 . Поскольку
. Поскольку 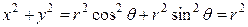 и
и  , уравнения окружностей, ограничивающих область интегрирования,
, уравнения окружностей, ограничивающих область интегрирования, 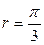 и
и  . Делаем замену переменных в двойном интеграле
. Делаем замену переменных в двойном интеграле 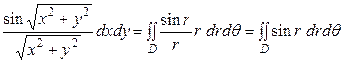 . Определимся с порядком интегрирования: пусть внешнее интегрирование происходит по
. Определимся с порядком интегрирования: пусть внешнее интегрирование происходит по 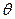 , тогда область интегрирования рассекается (штрихуется) лучами
, тогда область интегрирования рассекается (штрихуется) лучами 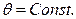 :
:
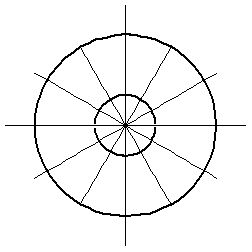
Рисунок 62.
Нетрудно заметить, что после перехода к полярным координатам область интегрирования проходится полностью, если изменять  от нуля до
от нуля до  , а
, а 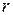 от
от 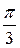 до
до  . Итак,
. Итак,
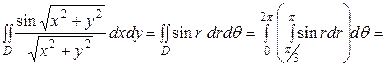
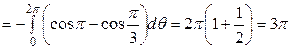 .
.
Пример 2. Вычислить интеграл  по области, ограниченной окружностью
по области, ограниченной окружностью 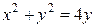 , ее каноническое уравнение
, ее каноническое уравнение 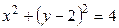 .
.
Переходим к полярной системе координат, уравнение окружности принимает вид  или
или 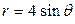 , интеграл
, интеграл
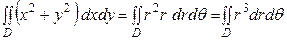 .
.
Выбираем внешнее интегрирование по  , тогда область интегрирования штрихуется следующим образом
, тогда область интегрирования штрихуется следующим образом

Рисунок 63.
Для прохождения всей области интегрирования внешний интеграл необходимо вычислять в пределах 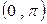 , внутренний - от полюса
, внутренний - от полюса 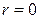 до линии выхода из области интегрирования
до линии выхода из области интегрирования 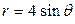 . Итак,
. Итак,
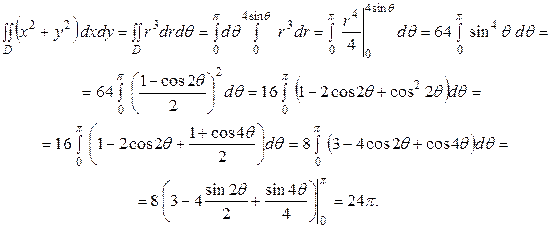
Примеры для самостоятельного решения
Вычислить двойные интегралы
18.5.  ,
,  область, ограниченная линиями
область, ограниченная линиями  .
.
Ответ 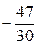 .
.
18.6. 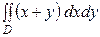 ,
,  область, ограниченная линиями
область, ограниченная линиями 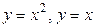 .
.
Ответ 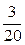 .
.
18.7.  ,
,  область, ограниченная окружностью
область, ограниченная окружностью  .
.
Ответ 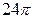 .
.
18.8.  ,
,  область, ограниченная линиями
область, ограниченная линиями  ,
,  ,
,


