 |
I. Понятие функционального уравнения
|
|
|
|
ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Автор работы: Багаутдинова Альбина,
ученица 11 «А» класса СОШ № 11
Научный руководитель: Петрова Ирина Владимировна,
учитель математики
Г. Зеленодольск
Содержание
Введение.......................................................................................................... 3
I. Понятие функционального уравнения...................................................... 4
II. Способы решения функциональных уравнений.................................... 6
1. Простейшие функциональные уравнения............................................... 6
2. Решение функциональных уравнений методом подстановки............ 7
3. Решение функциональных уравнений методом Коши......................... 16
4. Использование значений функции в некоторых точках....................... 18
5. Уравнение относительно f(x)..................................................................... 19
6. Графическое решение функциональных уравнений............................. 19
Заключение........................................................................................................ 21
Список использованной литературы……………………………….....….. 22
Приложения……………………………………………………………….... 23
Введение
Одно из важнейших математических умений, которым должны овладеть учащиеся средней школы, − умение решать уравнения. Корень уравнения находят в одно или более действий, многие текстовые задачи решаются алгебраическим способом, то есть уравнения одновременно сами по себе являются задачами и способами решения задач, умение решать которые необходимы всем учащимся школы. Но во время решения тренировочных заданий мне попалось уравнение, которое я решить не смогла. Как я узнала позже от учителя, это было функциональное уравнение.
Что же такое функциональные уравнения? И какие способы их решения существуют? Эти вопросы заинтересовали меня, и я решила провести исследование.
|
|
|
Актуальность работы заключается в том, что эта тема в школьном курсе математики не изучается в виду её сложности, а при поступлении в престижные ВУЗы, на олимпиадах, в заданиях части С ЕГЭ такие задачи встречаются.
Цель работы - выяснить, что является функциональным уравнением, найти способы решения и научиться применять их на практике.
Задачи исследования:
1. Изучение и анализ литературы;
2. Поиск способов решения функциональных уравнений;
3.Применение полученных знаний при решении функциональных уравнений.
Структура работы: введение, понятие функционального уравнения, способы решения функциональных уравнений, примеры решения функциональных уравнений, заключение.
I. Понятие функционального уравнения
Функциональное уравнение – это уравнение, которое содержит одну или несколько неизвестных функций (с заданными областями определения и значений).
Функция f(x) называется решением данного функционального уравнения, если она удовлетворяет ему при всех значениях аргумента в области её определения.
Решить функциональное уравнение – это, значит, найти все функции, которые тождественно ему удовлетворяют.
Функциональные уравнения возникают в самых различных областях математики, обычно в тех случаях, когда требуется описать все функции, обладающие заданными свойствами. Термин функциональное уравнение обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами неизвестной функции в уравнении являются не сами независимые переменные, а некоторые данные функции от них.
Некоторые функциональные уравнения знакомы нам еще из школьного курса. Это уравнения f(x) = f(-x), f(-x) = - f(x), f(x+T) = f(x), которые задают такие свойства функций, как чётность, нечётность, периодичность. Простым видом функциональных уравнений является реккурентное соотношение, знакомое нам по теме Последовательности, которое, говоря формально, содержит неизвестную функцию от целых чисел и оператор сдвига. (пример реккурентного соотношения: 
).
|
|
|
Задача решения функциональных уравнений является одной из самых старых в математическом анализе. Они появились почти одновременно с зачатками теории функций. Первый настоящий расцвет этой дисциплины связан с проблемой параллелограмма сил. Ещё в 1769 году Даламбер свёл обоснование закона сложения сил к решению функционального уравнения
(1)
То же уравнение и с той же целью было рассмотрено Пуассоном в 1804 году при некотором предположении аналитичности, между тем как в 1821 году Коши (1789 – 1857) нашёл общие решения этого уравнения, предполагая только непрерывность f(x):
.
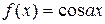
Даже известная формула неевклидовой геометрии для угла параллельности
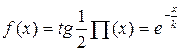
была получена Н. И. Лобачевским (1792 – 1856) из функционального уравнения
(2)
которое он решил методом, аналогичным методу Коши. Это уравнение можно привести к уравнению
.
Решение — 
.
Ряд геометрических задач, приводящих к функциональным уравнениям, рассматривал английский математик Ч. Баббедж (1792—1871). Он изучал, например, периодические кривые второго порядка, определяемые следующим свойством для любой пары точек кривой: если абсцисса второй точки равна ординате первой, то ордината второй точки равна абсциссе первой. Пусть такая кривая является графиком функции у = f(х); (х, f(х)) — произвольная ее точка. Тогда, согласно условию, точка с абсциссой f(х) имеет ординату х. Следовательно,
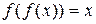(3)
Функциональному уравнению (3) удовлетворяют, в частности, функции:
,
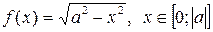Одними из простейших функциональных уравнений являются уравнения Коши
f(x+y) = f(x)+f(y), (4)
f(x+y) = f(x)·f(y), (5)
f(xy) = f(x)+f(y), (6)
f(xy) = f(x)·f(y), (7)
Эти уравнения Коши подробно изучил в своём (Курсе Анализа), изданном в 1821 году. Непрерывные решения этих четырёх основных уравнений имеют соответственно вид
, 
, 
, 
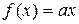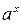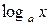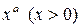
В классе разрывных функций могут быть и другие решения. Уравнение (4) ранее рассматривалось Лежандром и Гауссом при выводе основной теоремы проективной геометрии и при исследовании гауссовского закона распределения вероятностей.
|
|
|
Функциональное уравнение (4) было опять применено Г. Дарбу к проблеме параллелограмма сил и к основной теореме проективной геометрии; его главное достижение − значительное ослабление предположений. Мы знаем, что функциональное уравнение Коши (4) характеризует в классе непрерывных функций линейную однородную функцию f(x) = ax. Дарбу же показал, что всякое решение, непрерывное хотя бы в одной точке или же ограниченное сверху (или снизу) в произвольно малом интервале, также должно иметь вид f(x) = ax. Дальнейшие результаты по ослаблению предположений следовали быстро один за другим (интегрируемость, измеримость на множестве положительной меры и даже мажорируемость измеримой функцией). Возникает вопрос: существует ли хоть одна какая-нибудь аддитивная функция (т. е. удовлетворяющая (4)), отличная от линейной однородной. Найти такую функцию действительно нелегко! В ходе работы мы покажем, что при рациональных x значения любой аддитивной функции должны совпадать со значениями некоторой линейной однородной функции, т. е. f(x) = ax для x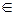 
Q. Казалось бы, что тогда f(x) = ax для всех действительных x. Если f(x) - непрерывна, то это действительно так, если же данное предположение отбросить - то нет. Первый пример отличного от f(x) = ax разрывного решения функционального уравнения (4) построил в 1905 году немецкий математик Г. Гамель с помощью введённого им базиса действительных чисел.
Многие функциональные уравнения не определяют конкретную функцию, а задают широкий класс функций, т. е. выражают свойство, характеризующее тот или иной класс функций. Например, функциональное уравнение f(x+1) = f(x) характеризует класс функций, имеющих период 1, а уравнение f(1+x) = f(1-x) - класс функций, симметричных относительно прямой x = 1, и т. д.
|
|
|
