 |
Решение функциональных уравнений методом подстановки
|
|
|
|
Заменяя некоторые переменные функционального уравнения либо конкретными значениями, либо какими-либо другими выражениями пытаемся либо упростить это уравнение, либо привести его к такому виду, что дальнейшее решение станет очевидным. Особенность применяемого метода как раз и состоит в том, что в ряде случаев он позволяет отыскать решения в классе всевозможных функций.
1. Найдите все функции, определённые на множестве 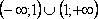 , удовлетворяющие соотношению
, удовлетворяющие соотношению 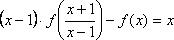 .
.
Решение:
Придадим x значение  . Получим
. Получим
 .
.
Отсюда  .
.
Получим систему 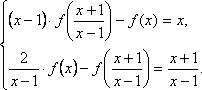

Из уравнения (1) выразим 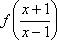 и подставим в уравнение (2).
и подставим в уравнение (2).
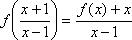 ;
; 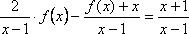 ;
;
Отсюда 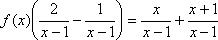 ;
;
 ;
;
 .
.
Проверим, действительно ли функция f(x) удовлетворяет уравнению 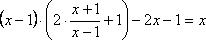 .
.
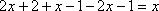
x=x - верно.
Ответ: 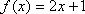 .
.
2. Найти функцию, удовлетворяющую уравнению
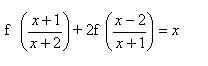
Решение:
1) Пусть
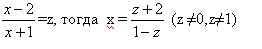
2) Подставим в исходное уравнение, получим

3)Заменим z на 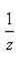 получим
получим 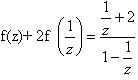
или после преобразований в правой части уравнения: 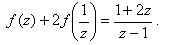
4)Итак, получили два уравнения:
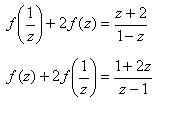
5)Умножим обе части 1-го уравнения на (-2) и сложим со 2-ым уравнением, получим:
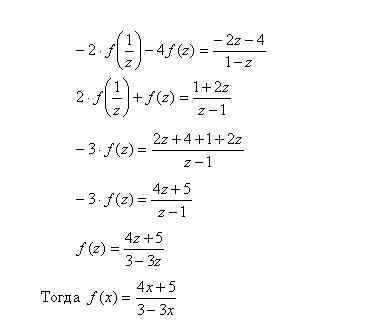
3. Пусть 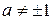 - некоторое действительное число. Найти функцию f(x), определённую для всех x ≠ 1 и удовлетворяющую уравнению
- некоторое действительное число. Найти функцию f(x), определённую для всех x ≠ 1 и удовлетворяющую уравнению
 ,где g – заданная функция, определённая при x ≠ 1.
,где g – заданная функция, определённая при x ≠ 1.
Решение: При замене
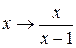 получаем систему
получаем систему
 .
.
решением которой при a2 ≠ 1 является функция
Ответ: 
4. Найти решение системы функциональных уравнений относительно неизвестных функций f(x) и g(x):
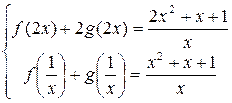
Решение:
В первом уравнении сделаем подстановку 2x = 1/z.
При этом

и первое уравнение принимает вид:
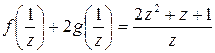 или
или

В результате получаем систему уравнений:

решение которой g(x) = 1/x, f(x) = x+1.
Ответ: g(x) = 1/x, f(x) = x+1.
5. Найдите все функции f: R à R, которые при всех х, у? R удовлетворяют уравнению f(х+у)=х+уf(х)+(1-х)у. (1)
|
|
|
Решение:
Пусть f − функция удовлетворяющая уравнению (1). Поскольку (1) выполняется при всех значениях переменных х и у, то оно будет выполнятся и при конкретных значениях этих переменных. Подставив, например, у = 0 в исходное уравнение, мы получим f(х)=х. Это равенство должно выполнятся при любом действительном х.
Таким образом, (1) => f(х)≡х или, иными словами, никакая функция кроме f(х)≡х не может удовлетворять уравнению (1). Это, тем не менее, не доказывает, что функция f(х)≡х является решением функционального уравнения (1). Непосредственная проверка показывает, что найденная функция действительно удовлетворяет уравнению при всех х,у? R.
6. Найдите все функции f: R à R, которые при всех х, у? R удовлетворяют уравнению f(х+у)=х+уf(х)+(1-sin х)у. (2)
Решение:
Точно также, как и в предыдущей задаче, устанавливаем, что для функции f, которая удовлетворяет (2), должно выполнятся тождество f(х)≡х. Однако, подставив функцию f(х)=х в (2), мы тождества не получим. Поскольку никакие другие функции также не могут быть решениями (2), то данное уравнение решений не имеет.
7. Найдите все функции f: R à R, которые при всех х, у? R удовлетворяют уравнению
f(х+у2+2у+1) = у4+4у3+2ху2+5у2+4ху+2у+х2+х+1. (3)
Решение:
Поскольку мы хотим получить значение f(х), попробуем избавится от слагаемого у2+2у+1 под знаком функции. Уравнение у2+2у+1=0 имеет одно решение у=-1. Подставляя у= -1 в (3) получаем f(х)= х2-х+1.
Ответ: f(х)= х2-х+1.
8. Найдите все функции f: R à R, которые при всех х, у? R удовлетворяют уравнению
f((х2+6х+6)у)=у2х4+12у2х3+48у2х2-4ух2+72у2х-24ух+36у2-24 (4)
Решение:
Как и в прошлой задаче, мы хотим получить под знаком функции свободную переменную (х или у). В данном случае, очевидно, проще получить у. Решив уравнение х2+6х+6)у=0 относительно х получаем х1= -1, х2= -5. Подстановка любого из этих значений в (4) дает нам f(у)=у2-4у.
9. Решите следующие функциональные уравнения.
|
|
|
а) f(x)+2f(1/x)=3x (x≠0)
б) f(х)+f(x-1/x)=2x (x≠0)
в) f(x+y)+f(x-y)=2f(x)cos y
Решение:
а) Положим у=1/x. Тогда f(1/y) + 2f(y) =3/y и f(y)+2f(1/y)=3y. Отсюда f(y)= 2/y – y.
б) Положим y=x-1/x, затем z=y-1/y. Получим систему трёх линейных уравнений относительно f(x), f(y), f(z), з которой находим
в) Положив у=π/2, получаем f(х+π/2) +f(x-π/2)=0 для любого х, откуда f(x+π)= - f(x). Заменив у на у+π/2, получаем
заменив теперь х- π/2 на х, имеем:
и с учетом предыдущего:
Положив х=0, получаем отсюда и из исходного уравнения:
Таким образом, искомая функция должна иметь вид a cos y +b sin y, где a,b – константы.
10. 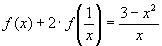
Решение: 1) Заменим  на
на 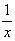 , получим
, получим 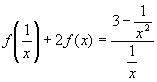 или
или  .
.
2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением: 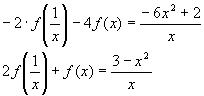
получаем:
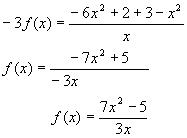
11. 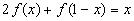 2
2
Решение: 1)Заменим в уравнении  на
на 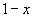 , получим
, получим 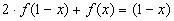 2.
2.
2) Умножим обе части исходного уравнения 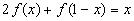 2 на (-2) и сложим с уравнением
2 на (-2) и сложим с уравнением 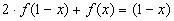 2,
2,
получим: 
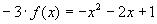

12. 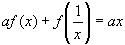
Решение:
1) Заменим в уравнение 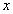 на
на 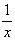 ,
, 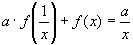 .
.
2)Умножим уравнение 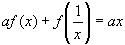 на
на  и вычтем из уравнения
и вычтем из уравнения 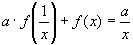 , получим -
, получим - 
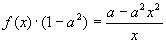
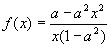 , где а
, где а 
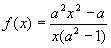
13.
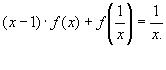
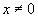
Решение:
1)Заменим в уравнении 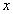 на
на 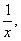 получим
получим 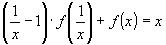 .
.
2)Выразим из исходного уравнения 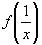 , получим
, получим 
или  .
.
3)Подставим 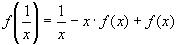 в уравнение
в уравнение 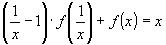 , получим
, получим  .
.
Выполним преобразования


14. 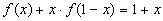
Решение:
1.Заменим 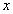 на
на 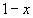 , получим
, получим 
2.Умножим обе части уравнения 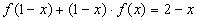 на
на  и вычтем из уравнения
и вычтем из уравнения 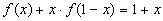
получим
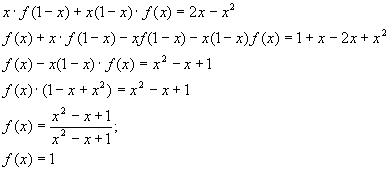
15. 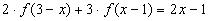
Решение: 1)Пусть 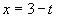 , тогда уравнение принимает вид:
, тогда уравнение принимает вид: 
2)Пусть 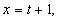 тогда исходное уравнение принимает вид:
тогда исходное уравнение принимает вид: 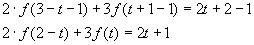
3)Умножим обе части уравнения из п.1 на 2, а обе части уравнения из п.2 на (-3) и почленно сложим получившиеся уравнения:
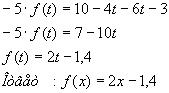
16. 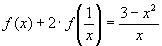
Решение:
1) Заменим 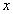 на
на 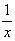 , получим
, получим 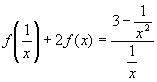 или
или  .
.
2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:
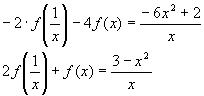
получаем:
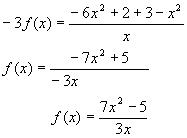
|
|
|


