 |
Раздел III. Показательные уравнения, неравенства, иррациональные неравенства и их решение.
|
|
|
|
Оглавление
Оглавление. 1
Раздел I. Тригонометрические уравнения и их решение. 2
Раздел II. Логарифмические уравнения и. 11
Неравенства и их решение. 11
Раздел III. Показательные уравнения, неравенства, иррациональные неравенства и их решение. 30
Раздел IV. Задачи по геометрии и их решение. 41
Раздел V. Задачи для самостоятельного решения. 54
Ответы к задачам для самостоятельного решения. 55
Список литературы.. 57
Раздел I. Тригонометрические уравнения и их решение.
№1. Решите уравнение: 
Решение:

 ;
;
1) 
Пусть 








2) 

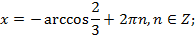

Ответ: 
№2 Решите уравнение: 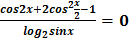 .
.
Решение: 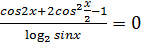
1. ОДЗ: 
2. 
Для решения применяем формулу 
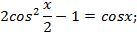

Пусть  тогда
тогда 


a) 

б) 
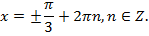
| y |
| x |
| 0 |
 /2 /2
|

|


|
3. С учетом ОДЗ имеем 
Ответ: 
№3 а) Решите уравнение:  ;
;
б) Найдите все корни этого уравнения, принадлежащие отрезку  .
.
Решение:



 , имеем:
, имеем:
 ,
, 
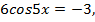


б) 1) 



при n =1, 
при n =2, 
2) 

При n =2, 
Ответ: а) 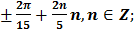 б)
б) 
№4. Решите уравнение: 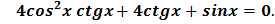
Решение:
Приведем  к общему знаменателю sinx:
к общему знаменателю sinx:
1) 

2) 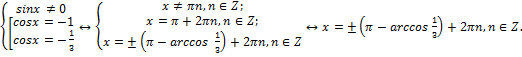
Ответ: 
№5. Решите уравнение: 
Решение:

Используем формулу синуса разности двух углов




т.к. 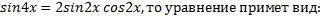


Решаем методом введения вспомогательного угла:
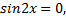 или
или  ,
,


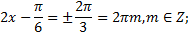


Ответ: 
№6. Решите уравнение: 
Решение:
 ,
,
Используем формулу косинуса разности двух углов


т.к. 


Решаем методом введения вспомогательного угла:
 или
или 





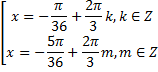
Можно и по-другому:

 , или
, или
 ,
,
 .
.
Ответ: 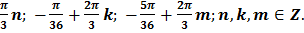
или 
№7. Решите уравнение: 
Решение:

Воспользуемся одной из формул разности одноименных функций и формулой синуса двойного угла.
|
|
|



 или 2)
или 2)  ,
,





Решение 1 и 2 уравнений можно записать как 
Решение исходного уравнения: 
Ответ: 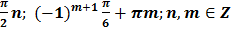 .
.
№8. Решите уравнение: 
Решение:
 ,
,





Пусть 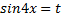 , тогда
, тогда



отсюда
 ,
,


Ответ: 
№9. Решите уравнение: 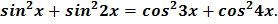
Решение:
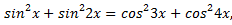
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
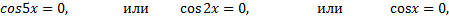


Решение уравнения  ,
,  – подмножество решений уравнения
– подмножество решений уравнения 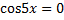 , поэтому решением заданного уравнения являются:
, поэтому решением заданного уравнения являются:  .
.
Ответ:  .
.
№10 а) Решите уравнение:  ;
;
б) Запишите множество решений, принадлежащих отрезку  .
.
Решение:
 ,
,
 ,
,
 ,
,
Введем замену: пусть  , тогда
, тогда
 ,
,
 ,
,
 ,
,
Возвращаемся к замене:
 ,
,
 ,
,
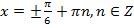 ,
,
при n=1:  ;
;
 .
.
Ответ: а)  ; б)
; б)  .
.
Раздел II. Логарифмические уравнения и неравенства и их решение.
№1. Решить неравенство: 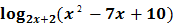 <
< 
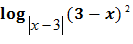 .
.
В ответе указать множество решений, сумму целых значений из этого множества.
Решение:
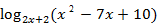 <
< 

1) ОДЗ:





Найдем решение системы при помощи числовой прямой

| X |
-1 -   2 5 2 5
|

X 
2) 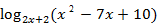 <
< 


 =
=  =
=  =1
=1
Запишем уравнение в упрощенном виде:
 < 1
< 1
 <
< 
а) 



б) 
Объединяя найденные множества решений, учитывая ОДЗ, получаем решение неравенства
-1 -  1 2 5 8 1 2 5 8
|
| Х |



6+7=13- сумма целых решений
Ответ:  ;
;
Сумма целых значений из множества решений 13.
№2. Решите уравнение.
2  -
-  -
-  =0.
=0.
Решение.
2  -
-  -
-  =0
=0
| -4 -2 -1 2 |


 x
x
x  (-
(-  -4)
-4)  (-4;-2)
(-4;-2)  (2;
(2;  ).
).
б) 2  = 2
= 2 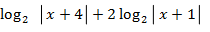
 =
= 
| xX |
 =
= 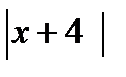


| -4 -2 -1 2 |
|
|
|
Нули подмодульных выражений
а) 
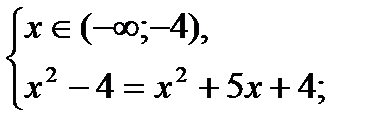

 нет решений
нет решений
б) 

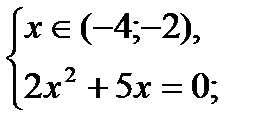

 x=-2,5
x=-2,5
в) 
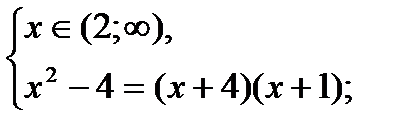




 нет решений
нет решений
x=-2,5 – решение исходного уравнения
Ответ: -2,5.
 №3. Решите уравнение 2
№3. Решите уравнение 2  -
-  -
-  =0.
=0.
Решение
а) Найдем область допустимых значений x:


-3 -  -2 -2    6 6          
|
x  ;
; 

б) 2  -
-  -
-  =0,
=0,
2  = 2
= 2  ,
,
 =
=  ),
),
X  -6=
-6=  ,
,
X  -6=
-6=  ,
,
X  -6=
-6=  Данное уравнение равносильно системе:
Данное уравнение равносильно системе:







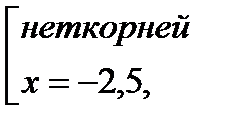
 .
.
Ответ: -2,5.
№4. Решите уравнение  .
.
Решение:
1) Найдем область допустимых значений:


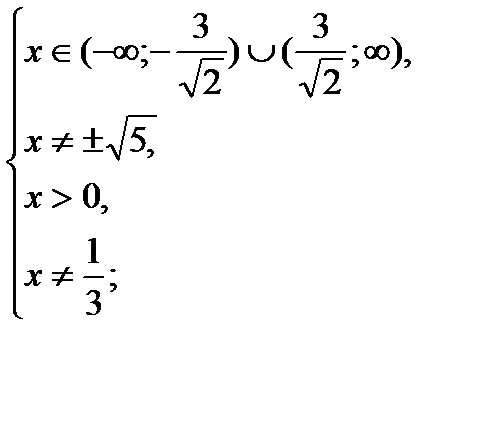




2) Решим, используя свойства логарифмов и формулу перехода к логарифму с другим основанием:
 = log3x7 +
= log3x7 + 
 = log3x7 +
= log3x7 + 
 = log3x21
= log3x21
2x2-9=3x
2x2-3x-9=0
D=9+72=81
х1=3  ОДЗ
ОДЗ
х2= -1,5- не удовлетворяет ОДЗ
Ответ: 3.
№5. При каких значениях х соответственные значения функций  log 2 x и g (x)= log 2 (3- x) будут отличаться меньше, чем на 1?
log 2 x и g (x)= log 2 (3- x) будут отличаться меньше, чем на 1?
Решение:


Используя определение и свойства логарифмов имеем систему неравенств


1) 
-1 < log2  < 1,
< 1,
log2  < log2
< log2 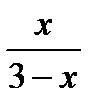 < log22,
< log22,
 <
<  < 2,
< 2,


 x
x  (1;2)
(1;2)
2) C учетом ОДЗ получаем систему уравнений

 1<x<2.
1<x<2.
Ответ: (1;2).
№6. Решить уравнение  .
.
Решение
Находим ОДЗ уравнения: х>0. Введем обозначение  , тогда уравнение примет вид
, тогда уравнение примет вид  или
или  (в силу свойства
(в силу свойства 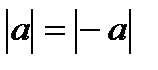 ). Рассмотрим три случая:
). Рассмотрим три случая:
· t  3, тогда по определению абсолютной величины имеем
3, тогда по определению абсолютной величины имеем  и
и  Подставляя в уравнение, получим t-1+2=t-3
Подставляя в уравнение, получим t-1+2=t-3  1=-3, что невозможно. Следовательно, решений нет.
1=-3, что невозможно. Следовательно, решений нет.
· 1  t<3, тогда
t<3, тогда  и
и  , уравнение примет вид t-1+2=3-t
, уравнение примет вид t-1+2=3-t  2t=2
2t=2  t=1
t=1 

· t<1  и 1-t+2=3-t
и 1-t+2=3-t  , т.е. уравнение верно при всех t<1, откуда
, т.е. уравнение верно при всех t<1, откуда  и имеем бесчисленно множество решений.
и имеем бесчисленно множество решений.
Объединив второй и третий случаи, получим ответ  .
.
Ответ:  .
.
№7. Решить уравнение  .
.
Решение:

1)Найдем область допустимых значений х:










Сравним  и
и  :
:


Следовательно, областью допустимых значений x является:
x  (
(
2)выполним преобразование, используя свойства логарифмов






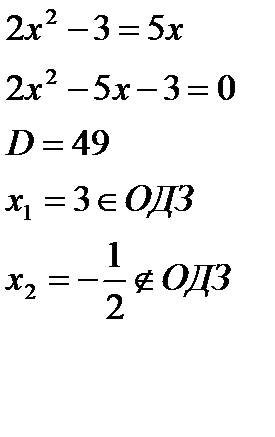
Ответ: 3.
№8. Решить уравнение  .
.
Решение:

1)Найдем область допустимых значений

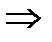




Сравним  и
и 

 =
=  =
=  ;
;


 .
.

Ответ: 2.
№9. Решите уравнение  .
.
|
|
|
Решение:

ОДЗ: 




Решаем уравнение, применяя свойства логарифмов.




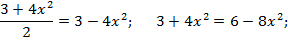
12  -3= 0;
-3= 0;  =
=  ;
; 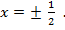

Ответ:  .
.
№10. Решите уравнение  ).
).
Решение:
 ).
).
ОДЗ: 



 x
x  (0;1)(1;
(0;1)(1; 
Решаем уравнение, применяя свойства логарифмов.
 =4
=4  + 2
+ 2 
 = 2 + 1 - 2
= 2 + 1 - 2  ,
,
 = 3 - 2
= 3 - 2  равносильно системе
равносильно системе





 ОДЗ,
ОДЗ,

Ответ: 
№ 11 Решите уравнение 
Решение: x-5>0 x>5 x>5
1) ОДЗ  >0 ⟹
>0 ⟹  x>-7 ⟹ x>-7 ⟹ x>5
x>-7 ⟹ x>-7 ⟹ x>5
lg  -lg2 ≠0
-lg2 ≠0 
 ≠ 2 x≠-3
≠ 2 x≠-3
2)lg8-lg(x-5)=lg  -lg2
-lg2
lg8+lg2=lg  + lg(x-5)
+ lg(x-5)
lg(8·2)=lg( (x-5))
(x-5))
16=  (x-5)
(x-5)
 ((x-5)
((x-5)  =16
=16
x>5
Можно методом подбора:
Пусть x=9, тогда
(9-5)  =16 –верное
=16 –верное
Поэтому x=9.
Ответ 9.
№12. Решить уравнение log  x + log
x + log  8 =3- log
8 =3- log 
 .
.
Решение:
log  x+ log
x+ log  8 =3-log
8 =3-log 

ОДЗ: x>0 ó x  (0;1)
(0;1)  (1;
(1;  )
)
x≠1
Применяя формулу logab=  рассмотрим:
рассмотрим:
1)log  x+
x+  =
=  =2log
=2log  x;
x;
2)log  8=
8=  =
= 
 =
=  =
=  ;
;
3)log 
 =
=  =
=  =-2*1/2log
=-2*1/2log 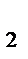 x=-log
x=-log  x.
x.
Решим уравнение
2log 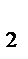 x+
x+  =3+log
=3+log 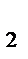 x.
x.
2 log  x-log
x-log  x+
x+  =3
=3
log  x+
x+  =3
=3
log  x+2=3log
x+2=3log  x
x
log 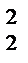 x-3log
x-3log  x+2=0
x+2=0
Пусть log  x=y, тогда
x=y, тогда
y  -3y+2=0
-3y+2=0
Д=9-8=1
y 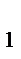 =
=  =2; y
=2; y 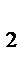 =
=  =1, отсюда
=1, отсюда
log  x=2 и log
x=2 и log  x=1
x=1
x=4  x=2
x=2 
Ответ: 2;4.
№ 13. Решите неравенство 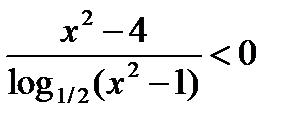 .
.
Решение: 

Решим методом интервалов.
1) (x-2)*(x+2)=0
x=2 или x=-2
2) log  (x
(x  -1)≠0
-1)≠0
a) ОДЗ x  -1>0
-1>0
(x-1)(x+1)>0
-1 1
x 
b) x  -1≠1
-1≠1
x  ≠2
≠2
x≠± 
3)
| - + - - + - - |
-2 -  -1 1
-1 1  2
2
x 
Ответ: x 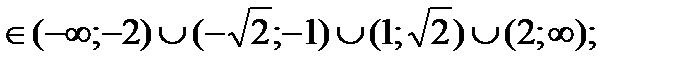
№14. Решите неравенство 5 log 8 (x 2 -15 x +56)  6+ log 8
6+ log 8 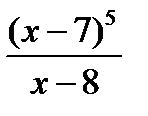 .
.
Решение:
5log8(x2-15x+56)  6+log8
6+log8 
Разложим на множители квадратный трехчлен x2-15x+56:
X2-15X+56=0
D=(-15)2-4  56=225-224=1
56=225-224=1
X1= 
 ;
;
X2=7;
X2-15X+56=(X-8)(X-7)
5log8(x-8)(x-7)


