 |
Раздел IV. Задачи по геометрии и их решение.
|
|
|
|
Задача №1
В единичном кубе ABCDA 1 B 1 C 1 D 1 найдите расстояние от точки D до плоскости (CAD 1).
Дано: Решение:
| D1 |
| A1 |
| C1 |
| B1 |
| K |
| O |
| A |
| D |
| C |
| B |
 (D, (CAD1))
(D, (CAD1))
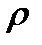 (D; (CAD1)) = DK (DK
(D; (CAD1)) = DK (DK  OD1)
OD1)
I способ. Работаем по формуле h=  , т.к.
, т.к.  OD1D – прямоугольный
OD1D – прямоугольный
D1 D=1; OD =  ; OD 1 =
; OD 1 =  =
=  из
из  ODD1 - прямоугольного
ODD1 - прямоугольного
KD = 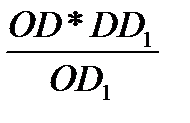 , KD =
, KD =  =
=  =
= 
II способ. 1)  ODD1 – прямоугольный
ODD1 – прямоугольный
sin  D1OD =
D1OD =  ; DD1 = 1; OD=
; DD1 = 1; OD= 
 BD=
BD=  ;
;
OD1 =  =
=  =
=  =
= 
sin D1OD= 1: 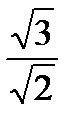 =
= 
2)  - прямоугольный
- прямоугольный
KD=OD sin KOD
KD=  *
*  =
=  =
= 
Ответ: 
Задача №2
В единичном кубе ABCDA 1 B 1 C 1 D 1 найдите расстояние между прямыми AD и CA 1.
Дано:  Решение:
Решение:
AB=1. A1 D1
Определить:  (AD,CA1) O
(AD,CA1) O
B h C
A D
1)AD и CA1-скрещивающиеся прямые. За расстояние между скрещивающимися прямыми принимают расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую, параллельно первой. Но (A1AC) не параллельна AD. В этом случае расстояние между скрещивающимися прямыми – это расстояние от точки одной прямой до другой, т.е. это длина перпендикуляра от точки одной прямой до другой. За данную точку удобно взять точку пересечения диагоналей плоскости A1AC, т.е. точку О, О- точка пересечения всех диагоналей куба (проведем B1D).
|
|
|
2)  (AD; A1C)=
(AD; A1C)=  (O; AD)= OK, т.к. OK
(O; AD)= OK, т.к. OK  AD.
AD.
 AOD- равнобедренный, OK-высота, медиана и биссектриса
AOD- равнобедренный, OK-высота, медиана и биссектриса  AOD.
AOD.
OK=  AO=
AO=  , AC1=A1C=B1D=
, AC1=A1C=B1D=  , AO=
, AO=  ,
,
AK=  ; OK=
; OK=  =
=  =
=  ;
;
 1C)=
1C)=  .
.
Ответ:  .
.
Задача №3
В правильной треугольной призме ABCA 1 B 1 C 1, стороны основания которой равны 2, а боковые ребра 3, найдите расстояние между прямыми AA 1 и BC 1.
Дано:  Решение:
Решение:
ABCA1B1C1- правильная
треугольная призма А1 С1
AB=2, AA1 =3; 3 В1
Определить:  (AA1;BC1)
(AA1;BC1)
| К |
| 2 |
| В |
1)AA1, BC1- скрещивающиеся прямые. За расстояние между скрещивающимися прямыми принимают расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую, параллельно первой.
AA1 || (B1BC). 
2)  (AA1; BC1) =
(AA1; BC1) =  (AA1; (BB1C1))=AK, где AK
(AA1; (BB1C1))=AK, где AK  (BB1C), т.к
(BB1C), т.к
а) B1B  (ABC)=
(ABC)=  BB
BB  AK;
AK;
б) AK  BC.
BC.
3)AK=  , где a=2, т.к.
, где a=2, т.к.  -правильный.
-правильный.
AK=  , значит,
, значит,  (AA1, BC1)=
(AA1, BC1)=  .
.
Ответ: 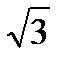 .
.
Задача №4
В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите косинус угла между прямой АС1 и плоскостью ВВ1С1.
| В1 |
| А1 |
| С1 |
|
|
|
| 1 |
АА1=1
| А |
| В |
| 1 |
| К |
| С |
1) Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость
АК  ВС С1К – проекции АС1 на (ВСС1)
ВС С1К – проекции АС1 на (ВСС1)  (АС1; (ВСС1)) =
(АС1; (ВСС1)) =  (АС1; С1К) =
(АС1; С1К) = 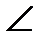 АС1К.
АС1К.
2) Косинус угла АС1К можно найти по теореме косинусов:
АК2=АС12+С1К2-2АС1*С1К cos AC1K.
а) АК=  из правильного
из правильного  АВС по формуле h=
АВС по формуле h= 
б) АС1=  из прямоугольного
из прямоугольного  АСС1;
АСС1;
в) С1К=  =
=  из прямоугольного
из прямоугольного  С1СК.
С1СК.
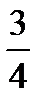 =2+
=2+  -2
-2  *
*  cos AC1K;
cos AC1K;
cos AC1K= 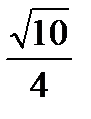 , значит, cos (АС1;(ВВ1С1)))=
, значит, cos (АС1;(ВВ1С1)))=  .
.
Ответ: 
Задача №5
Сторона основания правильной треугольной призмы АВСА1В1С1 равна 2  , а диагональ боковой грани равна 13. Найдите угол между плоскостью С1АВ и плоскостью основания призмы.
, а диагональ боковой грани равна 13. Найдите угол между плоскостью С1АВ и плоскостью основания призмы.
Дано: Решение:
АВСА1В1С1 – правильная A1 C1
треугольная призма
АВ=2  B1
B1 
ВС1=13 A C
Определить: K 2 
 ((С1АВ);(АВС)). B
((С1АВ);(АВС)). B
1) Угол между двумя плоскостями С1АВ и АВС с их общей границей называют двугранным углом. 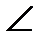 С1АВС – двугранный. Градусной мерой двугранного угла называется градусная мера его линейного угла.
С1АВС – двугранный. Градусной мерой двугранного угла называется градусная мера его линейного угла.
 ((С1АВ);(АВС))=
((С1АВ);(АВС))=  С1КС, т.к. СК
С1КС, т.к. СК  АВ, СК – проекция С1К, поэтому С1К
АВ, СК – проекция С1К, поэтому С1К  АВ.
АВ.
2)Рассмотрим  С1КС – прямоугольный и найдем tg C1KC =
С1КС – прямоугольный и найдем tg C1KC = 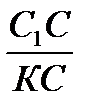 .
.
С1С=  =
=  =
=  =3
=3 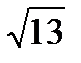 из прямоугольного
из прямоугольного  ВС1С.
ВС1С.
КС=  ; КС=
; КС=  =
=  - из правильного
- из правильного  АВС.
АВС.
tg C1KC =  =
=  =
=  ;
;
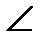 С1КС = 60о
С1КС = 60о 
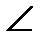 ((С1АВ); (АВС))=60о
((С1АВ); (АВС))=60о
Ответ:60о.
Задача №6
Диагонали трапеции СЕКМ (ЕК и СМ – основания) пересекаются в точке О. Площадь треугольника СОЕ равна 16, СО = 2 ОК. Найдите площадь трапеции.
|
|
|
Дано: Решение:
СЕКМ – трапеция
ЕК, СМ – основания
СК  ЕМ=О E K
ЕМ=О E K
S  =16 h
=16 h
СО=2ОК S=16 O h1
Определить:
Sтрапеции C M
1)S 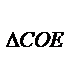 =
=  CO*h, S
CO*h, S  =16, OK=
=16, OK=  CO
CO
2)S  =
=  OK*h=
OK*h=  *CO*h=
*CO*h= 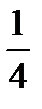 *СО*h=
*СО*h=  *16=8, где h – высота
*16=8, где h – высота  и
и  .
.
3)  подобен
подобен  МОС по 2 углам (
МОС по 2 углам ( ЕОК=
ЕОК=  СОМ, как вертикальные,
СОМ, как вертикальные,
 ОЕК=
ОЕК=  ОМС, как накрест лежащие при ЕК ||CM и секущей ЕМ) с коэффициентом подобия
ОМС, как накрест лежащие при ЕК ||CM и секущей ЕМ) с коэффициентом подобия
 =
= 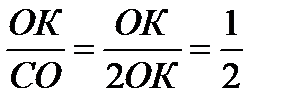 ;
;
 =
=  , поэтому
, поэтому  =(
=( )2=
)2=  , следовательно,
, следовательно,  =
=  ; S
; S 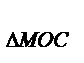 =32.
=32.
 S
S  =
= 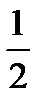 h1*OK=
h1*OK=  *h1*
*h1*  CO=
CO=  S
S  =16, т.к. h1 – высота
=16, т.к. h1 – высота  и
и  .
.
 Sтрап=16+8+32+16=72.
Sтрап=16+8+32+16=72.
 .
.
Задача №7
Основанием прямой призмы АВС DA 1 B 1 C 1 D 1 является прямоугольник ABCD, стороны которого равны 6  и 12
и 12 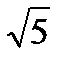 . Высота призмы равна 8. Секущая плоскость проходит через вершину D 1 и середины ребер AD и CD. Найдите косинус угла между плоскостью основания и плоскостью сечения.
. Высота призмы равна 8. Секущая плоскость проходит через вершину D 1 и середины ребер AD и CD. Найдите косинус угла между плоскостью основания и плоскостью сечения.
Дано: Решение:
| 15 |
| M |
| D1 |
| h |
| p |
| N |
| x |
| A1 |
| B1 |
| B |
| C1 |
| D1 |
| A |
| M |
| D |
| C |
| O |
| P |
| N |
| 8 |

|

|
ABCD- прямоугольник
DС=6 
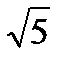
DD1=8
М-середина DА
N-середина DC
(D1NM)-секущая
|
|
|
Определить
сos ((ABC),(D1NM)).
Заметим, что сos ((ABC),(D1NM))= сos D1PD= сos  , где D1P
, где D1P  NM, DP
NM, DP  NM,
NM,  D1PD -линейный угол двугранного
D1PD -линейный угол двугранного  D1NMD.
D1NMD.
1) DB=AC=  =30, NM=15, D1P=h, P
=30, NM=15, D1P=h, P  DB. NP
DB. NP  PM.
PM.
2) а) ND1=  =
=  из
из  D1DN-прямоугольного.
D1DN-прямоугольного.
б) MD1=  =
=  из
из  D1DM- прямоугольного.
D1DM- прямоугольного.
3)  ND1M, NP=x, тогда
ND1M, NP=x, тогда
109-х2=244-(15-х)2 ,
109-х2=244-225+30х-х2,
х=3, т.е. NP=3.
4) h=D1P= 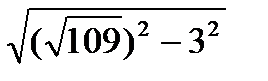 =10 из
=10 из  DNP - прямоугольного
DNP - прямоугольного
5) sin  =
=  ; sin
; sin  =
=  = 0.8
= 0.8
6) сos  =
= 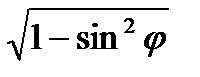 из
из  D1DP; сos
D1DP; сos  =0,6
=0,6
Ответ: сos ((ABC),(D1NM)) =0,6.
Задача №8
Трапеция ABCD вписана в окружность. Найдите среднюю линию трапеции, если ее большее основание AD равно 15, синус угла BAC равен  , синус угла ABD равен
, синус угла ABD равен  .
.
Дано:
ABCD – трапеция, вписанная Решение:
в окружность,
| B |
| C |
| D |
| A |
| K |
| L |
N 
|
sin ABD= 
Определить:
Среднюю линию трапеции
1) ABCD - равнобедренная трапеция.
а)  ABN=
ABN=  DCN по 2 признаку равенства треугольников (AB=CD;
DCN по 2 признаку равенства треугольников (AB=CD;
 BAC=
BAC=  BDC, как вписанные, опирающиеся на дугу BC; аналогично,
BDC, как вписанные, опирающиеся на дугу BC; аналогично,
 ABD=
ABD=  ACD). Следовательно, BN=NC, AN=ND.
ACD). Следовательно, BN=NC, AN=ND.
б)  BCN
BCN 
 DAN, т.к.
DAN, т.к.  BNC=
BNC=  AND, как вертикальные, и
AND, как вертикальные, и  =
=  .
.
2) По теореме синусов:
 =
=  ;
;  =
=  ;
;  =
=  ;
;  =
= 

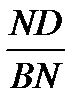 =
=  .
.
3)  =
=  =
= 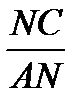 ;
;  =
=  , но AD=15, поэтому
, но AD=15, поэтому  =
= 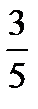 ; BC=9.
; BC=9.
4) Найдем среднюю линию трапеции ABCD.
KL=  ; KL=
; KL= 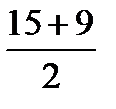 = 12.
= 12.
Ответ: средняя линия трапеции равна 12.
Задача №9
В правильной 6-угольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, все ребра которой равны 2, найдите расстояние от точки В до прямой A 1 F 1.
Решение:
| F1 |
| A1 |
| E1 |
| D1 |
| C1 |
| B1 |
| О |
| H |
| D |
| C |
| 2 |
D C
1)  (В,А1F1)=
(В,А1F1)=  (BE,A1F1), где ВЕ||A1F1,B
(BE,A1F1), где ВЕ||A1F1,B  BE, т.к. ВЕ||AF, AF||A1F1.
BE, т.к. ВЕ||AF, AF||A1F1.
2) A1H  BE, поэтому
BE, поэтому  (ВЕ,А1F1)=A1H.
(ВЕ,А1F1)=A1H.
3)  A1AH – прямоугольный. А1Н =
A1AH – прямоугольный. А1Н =  , где АН – проекция А1Н на плоскость.
, где АН – проекция А1Н на плоскость.
4) а)  АНВ – прямоугольный, sin60o =
АНВ – прямоугольный, sin60o =  ;
;  ; АН =
; АН = 
Или
б)  ОАВ – равносторонний. АН (высота) =
ОАВ – равносторонний. АН (высота) = 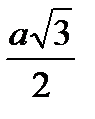 ; АН =
; АН =  =
=  .
.
Значит, А1Н =  =
=  .
.
Ответ:  .
.
Задача №10
В правильной 6-угольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, стороны основания которой равны 3, а боковые ребра 4, найдите расстояние от точки С до прямой E 1 D 1.
| E |
| D |
| F |
| C |
| B |
| A |
F1 C1
|
|
|
A1 B1
4
E D
| В |
| А |
| 3 |
За расстояние от С до E1D1 берем расстояние между Е1D1 и FC, 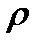 (E1D1;FC) = D1H, где
(E1D1;FC) = D1H, где
D1H  FC.
FC.
Задача №11
В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, стороны основания которой равны 4, а боковые ребра равны 3, найдите расстояние от точки С до прямой А1В1.
| B1 |
| A1 |
| H |
| B |
| F1 |
| E1 |
| F |
| E |
| D1 |
| C1 |
| C |
| D |
| A |
1) Расстояние от точки до прямой есть расстояние между двумя параллельными прямыми, на одной из которых лежит точка.
(А1В1 || AB, AB || FC) 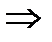 A1B1 || FC.
A1B1 || FC.  (C; A1B1)=
(C; A1B1)=  (FC; A1B1)= B1H, где В1Н
(FC; A1B1)= B1H, где В1Н  А1В1.
А1В1.
2)
| B |
| A |
 В1НВ – прямоугольный. В1Н=
В1НВ – прямоугольный. В1Н= 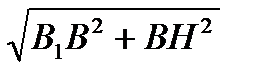 , ВН из
, ВН из  ВНС – прямоугольного (ВН – проекция В1Н).
ВНС – прямоугольного (ВН – проекция В1Н).
| H |
| H |
| C |
| F |


| D |
| E |
sin 60  =
=  ;
;  =
=  ; НВ=2
; НВ=2  . В1Н=
. В1Н=  =
=  =
=  .
.
Ответ:  .
.
Задача №12
В правильной четырехугольной пирамиде MABCD с вершиной М, стороны основания равны 6, а боковые ребра равны 5. Найдите площадь сечения пирамиды плоскостью, проходящей через точку А и середину ребра МС, параллельно прямой BD.
Дано: Решение:
| M |
| L |
| K |
| R |
| N |
| C |
| B |
| o |
| A |
| D |
параллельно BD.
1)Sсеч=  RK*LN+
RK*LN+  AR*LN=
AR*LN=  LN(RK+AR) =
LN(RK+AR) =  LN*AK;
LN*AK;
2)  AMC; OM, AK-медианы. AK=AR+RK; RK=
AMC; OM, AK-медианы. AK=AR+RK; RK=  AR, из
AR, из  AOR – прямоугольного. AR=
AOR – прямоугольного. AR=  , AO=
, AO=  AC; OR=
AC; OR= 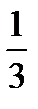 OM; AC=
OM; AC=  =6
=6  ; AO=3
; AO=3 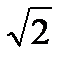
OM=  ; OM=
; OM=  ; OR=
; OR= 
AR=  =
=  RK=
RK=  AK=
AK=  ;
;
3)  LNM подобен
LNM подобен  BDM по двум углам; K=
BDM по двум углам; K=  (MO – медиана, AK–медиана из
(MO – медиана, AK–медиана из  AMC,
AMC,  )
)
LN=  BD, т.е. LN=
BD, т.е. LN=  *
*  ;
;
4) Sсеч=  ;
;
Ответ:  Sсеч= 13
Sсеч= 13  .
.
Задача №13
В правильной четырехугольной пирамиде MABCD с вершиной М стороны основания равны 3, а боковые ребра 8. Найдите площадь сечения пирамиды плоскостью проходящей через точку В и середину ребра MD, параллельно прямой AC.
| M |
| P |
| N |
| K |
| S |
| A |
| D |
| B |
| O |
| C |
параллельна ФС
Определить: Sсеч
1)Сечение правильной пирамиды – KPSB, где KB=B S из равенства треугольников CKB и ASB, аналогично, KP=PS. PM- высота (медиана)равнобедренного треугольника  KPS, BM-высота(медиана)
KPS, BM-высота(медиана)  KBS, т.е. PM
KBS, т.е. PM  KS и BM
KS и BM  KS.
KS.
Sсеч=  KS*PM+
KS*PM+  KS*BM=
KS*BM=  KS*PB;
KS*PB;
2) KS||AC по условию; B  DMB MO-медиана, BP-медиана, т.е. NO=
DMB MO-медиана, BP-медиана, т.е. NO=  ;
;
 KMS подобен
KMS подобен  CMA c K=
CMA c K= 
 KS=
KS=  AC; AC=
AC; AC=  ; KS=
; KS=  ;
;
3) MO=  ;
;
OB=  ;
;
4) NB= 
NB= 
PN=  BP-медиана
BP-медиана  DMB; PB=
DMB; PB=  ;
;
5)Sсеч= 
Ответ:  .
.
|
|
|
12 |


