 |
Тема 10. Кратные интегралы
|
|
|
|
1. Задачи, приводящие к двойному интегралу. Двойной интеграл и его свойства. Вычисление двойного интеграла повторным интегрированием в декартовых и полярных координатах. Изменение порядка интегрирования.
2. Тройной интеграл и его свойства. Вычисление тройных интегралов повторным интегрированием в декартовых и цилиндрических координатах.
3. Геометрические и физические приложения кратных интегралов.
Тема 11. Криволинейные и поверхностные интегралы и теория поля
1. Криволинейные интегралы первого и второго рода, их основные свойства и вычисление.
2. Понятие о поверхностных интегралах, их свойства и вычисление.
3. Скалярные и векторные поля. Потенциальные и соленоидальные поля.
4. Поток векторного поля через ориентированную поверхность, его физический смысл. Дивергенция векторного поля, ее физический смысли вычисление.
5. Формула Грина. Условие независимости криволинейного интеграла второго рода от пути интегрирования. Нахождение функции по ее полному дифференциалу.
Тема 12. Теория вероятностей
1. Предмет теории вероятностей. Понятие случайного события. Классификация случайных событий. Пространство элементарных событий.
2. Классическое определение вероятности. Непосредственный подсчет вероятности. Статистическая вероятность.
3. Сумма и произведение событий и их свойства. Геометрическая интерпретация. Теорема сложения вероятностей несовместных событий. Зависимые и независимые события. Условная вероятность. Теорема умножения вероятностей. Теорема сложения вероятностей совместных событий.
4. Формула полной вероятности. Формула Байеса. Схема Бернулли. Формула Бернулли. Предельные теоремы: Пуассона, локальная и интегральная теоремы Муавра – Лапласа.
|
|
|
5. Понятие случайной величины. Типы случайных величин. Дискретная случайная величина. Ряд распределения и его свойства. Интегральная функция распределения случайной величины и ее свойства. Числовые характеристики дискретной случайной величины: математическое ожидание, дисперсия, среднеквадратическое отклонение и их свойства.
6. Непрерывная случайная величина. Интегральная и дифференциальная функции распределения и их свойства. Числовые характеристики непрерывной случайной величины.
7. Законы распределения случайных величин и их числовые характеристики (биномиальный, Пуассона, равномерный, показательный, нормальный). Функция Лапласа и ее свойства. Правило трех сигм и его практическое значение.
8. Двумерные случайные величины. Дискретные и непрерывные. Одномерные составляющие. Числовые характеристики двумерной случайной величины.
Тема 13. Элементы математической статистики
1. Предмет математической статистики. Генеральная совокупность, выборочный метод. Вариационный ряд. Статистическое распределение выборки. Интервальный статистический ряд. Полигон и гистограмма. Эмпирическая функция распределения.
2. Статистические оценки параметров и определение закона распределения генеральной совокупности. Точечные и интервальные оценки. Свойства точечных оценок (статистик): несмещенность, состоятельность и эффективность. Точечные оценки математического ожидания, дисперсии и среднего квадратического отклонения генеральной совокупности. Исправленная выборочная дисперсия.
3. Интервальные оценки параметров генеральной совокупности. Доверительная вероятность. Доверительные интервалы для оценивания математического ожидания нормально распределенной генеральной совокупности.
4. Статистические гипотезы: параметрические и непараметрические. Статистические критерии проверки гипотез. Уровень значимости. Статистическая проверка непараметрических гипотез. Критерий согласия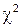 
Пирсона.
|
|
|
5. Элементы корреляционного и регрессионного анализа. Функциональная, статистическая и корреляционная зависимости. Линейная корреляционная зависимость и прямые регрессии. Выборочный коэффициент корреляции и его свойства. Проверка значимости коэффициента корреляции.
6. Эмпирические зависимости. Метод наименьших квадратов.
Тема 14. Элементы линейного программирования
1. Постановка задачи линейного программирования.
2. Графический метод решения задач линейного программирования.
3. Симплекс-метод.
4. Транспортная задача. Метод потенциалов решения транспортной задачи.
|
|
|
