 |
Решение уравнений средствами Mathcad
|
|
|
|
Лабораторная работа №3
РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Теоретические сведения
Уравнение – это равенство, которое выполняется лишь при некоторых значениях переменных, которые входят в уравнение.
Нелинейное уравнение – уравнение, в котором неизвестное находится в степени, не равной 1, или является аргументом какой-то функции.
Общий вид нелинейного уравнения:
где 
– некоторая нелинейная функция.
Если функция непрерывна на отрезке 
, то уравнение может иметь корни на этом отрезке при выполнении двух условий:
1) функция меняет знак на отрезке . Это легко проверить выполнением неравенства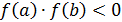 
;
2) первая и вторая производная сохраняют знак на всем отрезке.
Если какая-либо точка 
преобразовывает уравнение в равенство, то точка называется корнем нелинейного уравнения. Геометрически точка соответствует точке, в которой график функции 
пересекается с осью 
.
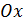Приближенное нахождение действительных корней состоит из 2 этапов:
1. Отделение корня (нахождение промежутка, в котором существует корень)
2. Уточнение корней с заданной степенью точности.
Для отделения корней применяют следующие способы:
- графический метод;
- табулирование функции;
- формулы Лагранжа для полиномов.
Для уточнения корней применяют следующие численные методы:
- метод половинного деления (дихотомии или бисекции);
- метод хорд;
- метод Ньютона (касательных);
- метод итераций или последовательных приближений;
Метод половинного деления
Дано: уравнение и интервал .
Находим точку 
:
Выполняем проверку: если 
, то тогда 
, а если 
, то тогда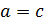 
. Если такую проверку сделать многократно, то мы будем сужать интервал до тех пор пока не найдем такую точку, для которой значение функции будет равно нулю, а модуль не будет превышать заданную точность 
.
|
|
|
Метод хорд.
Суть метода состоит в лианезации кривой хордой. Решение задачи покажет уравнение прямой, проходящей через 2 точк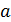и 
и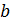 
:
Выбираем тот из промежутков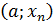 
или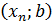 
, на концах которого знаки противоположны.
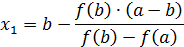
С выбранным промежутком повторяем те же действия, до тех пор, пока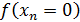 
и модуль не превышает заданной точности.
После многократных повторений получаем конечную формулу:
при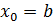 
.
Метод касательных.
Суть метода состоит в лианезации кривой касательной. Касательную проводят в том конце кривой, где знак второй производной совпадает со знаком функции, то есть:
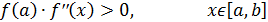
или
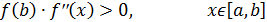
Решением является точка пересечения касательной с 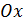. Решение получают из уравнения касательной, проходящей через соответствующую точку. После многократного повторения получаем конечную формулу:
Действия повторяются до тех пор, пока 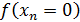и модуль не превышает заданной точности.
Итерационный метод.
Для использования итерационного метода разбиваем таким образом, чтобы можно было записать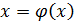 
.
Итерационный процесс записывается следующим образом:
Условием сходимости итерационного процесса является:
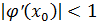
или
Решение уравнений средствами Mathcad
Как известно, многие уравнения не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Такие уравнения могут решаться численными методами с заданной точностью (не более значения заданного системной переменной TOL).
Для уравнений вида решение в Mathcad находится с помощью функции 
Возвращает значение 
, принадлежащее отрезку , при котором выражение или функция обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр.
Аргументы:
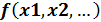– функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.
|
|
|
– имя переменной, которая используется в выражении. Этой переменной перед использованием функции 
необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.
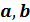– необязательны, если используются, то должны быть вещественными числами, причем 
.
Наиболее распространен графический метод определения начальных приближений. Принимая во внимание, что действительные корни уравнения – это точки пересечения графика функции с осью абсцисс, достаточно построить график функции и отметить точки пересечения с осью , или отметить на оси отрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив уравнение равносильным ему уравнением:
где функци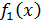и 
и 
– более простые, чем функция . Тогда, построив графики функций 
и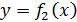 
, искомые корни получим как абсциссы точек пересечения этих графиков.
Отсутствие сходимости функции
Если после многих итераций Mathcad не находит подходящего приближения, то появится сообщение 
(отсутствует сходимость). Эта ошибка может быть вызвана следующими причинами:
- уравнение не имеет корней;
- корни уравнения расположены далеко от начального приближения;
- выражение имеет локальные 
и 
между начальным приближением и корнями;
- выражение имеет разрывы между начальными приближениями и корнями;
- выражение имеет комплексный корень, но начальное приближение было вещественным.
Чтобы установить причину ошибки, исследуйте график . Он поможет выяснить наличие корней уравнения и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет сходиться.
Рекомендации по использованию функции
Для изменения точности, с которой функция ищет корень, нужно изменить значение системной переменной TOL. Если значение TOL увеличивается, функция будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, то функция будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида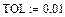 
. Чтобы изменить значение TOL для всего рабочего документа, измените его настройки.
|
|
|
Если два корня расположены близко друг от друга, следует уменьшить TOL, чтобы различить их.
|
|
|
