 |
Последовательность выполнения работы
|
|
|
|
Задание 1. Решить уравнение 
с помощью функции 
.
Решение приведено на рис. 2.1
Рис. 2.1 – Решение уравнения средствами Mathcad
Задание 2. Графически отделить корни уравнения 
.
Решение: перепишем исходное уравнение в виде равенства:
Отсюда ясно, что корни исходного уравнения могут быть найдены как абсциссы точек пересечения логарифмической кривой 
и гиперболы 
. Построив эти кривые, приближенно найдем единственный корень 
исходного уравнения или определим содержащий его отрезок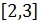 
. Решение приведено на рис. 2.2
Рис. 2.2 – Решение задания 2
Задание 3. Найти корни полинома 
. Решение приведено на рис. 2.3
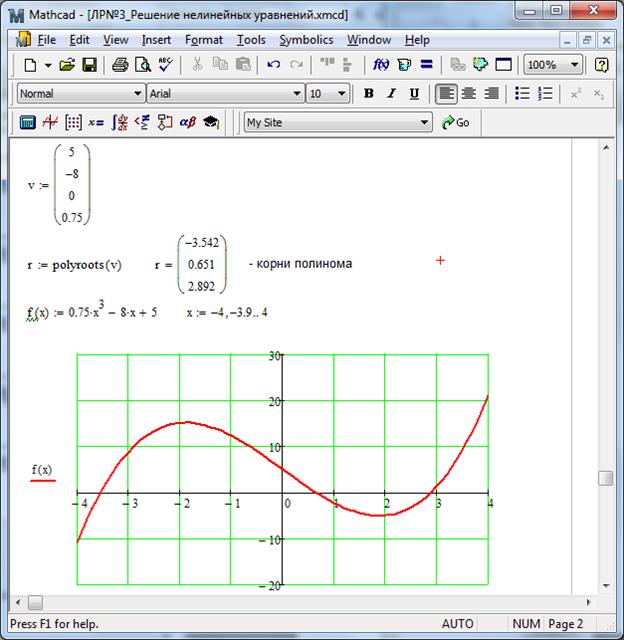
Рис. 2.3 – Решение задания 3
Задание 4. Дано уравнение 
.
Задание: 1) отделить корни этого уравнения графически.
2) уточнить их методом Ньютона с точностью до 
.
Решение приведено на рис. 2.4.
Рис. 2.4 – Решение задания 4 (начало)
Рис. 2.5 – Решение задания 4 (продолжение)
Рис. 2.6 – Решение задания 4 (окончание)
Задание 5. Дано уравнение: 
Задание: 1) отделить корни этого уравнения графически.
2) уточнить их методом хорд с точностью до 
.
Решение приведено на рис. 2.7.
Рис. 2.7 – Решение задания 5 (начало)
Рис. 2.8 – Решение задания 5 (продолжение)
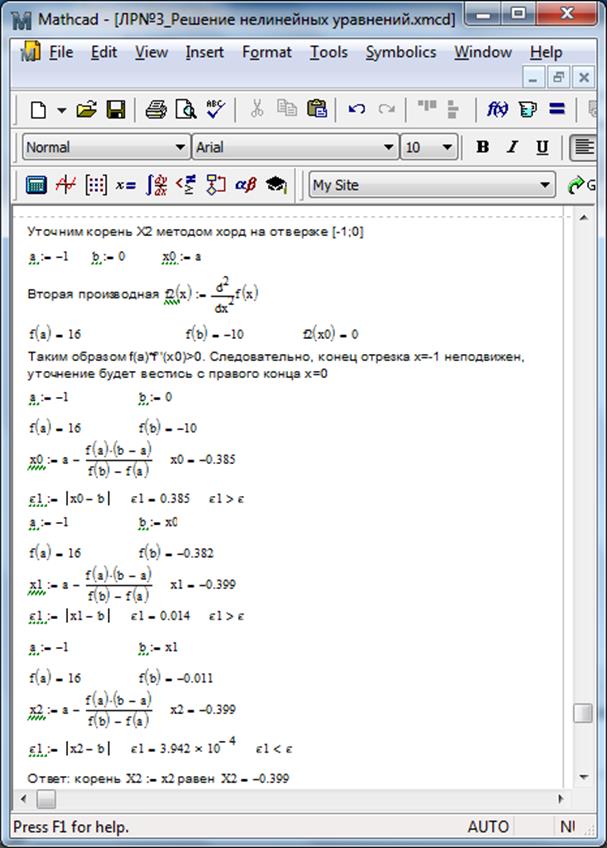
Рис. 2.9 – Решение задания 5 (продолжение)
Рис. 2.10 – Решение задания 5 (окончание)
Задание 6. Найти корень нелинейного уравнения
методом половинного деления с точностью 
.
Решение. Отделим корень уравнения на отрезке 
графическим методом. Для этого табулируем функцию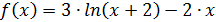 
на данном отрезке. Имеем , 
, 
, 
Выделим отрезок 
, содержащий изолированный корень, для уточнения которого применим метод половинного деления по схеме
где 
. Полагая 
, а также условие остановки деления отрезка пополам 
, составим таблицу
|
|
|
| 
| 
| 
| 
| 
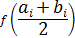
| корень | погрешность | Усл.ост. |
| 1,00000000 | 3,00000000 | 2,00000000 | 1,29583687 | -1,17168626 | 0,15888308 | 1,00000000 | нет | |
| 2,00000000 | 3,00000000 | 2,50000000 | 0,15888308 | -1,17168626 | -0,48776781 | 0,50000000 | нет | |
| 2,00000000 | 2,50000000 | 2,25000000 | 0,15888308 | -0,48776781 | -0,15924305 | 0,25000000 | нет | |
| 2,00000000 | 2,25000000 | 2,12500000 | 0,15888308 | -0,15924305 | 0,00119806 | 0,12500000 | нет | |
| 2,12500000 | 2,25000000 | 2,18750000 | 0,00119806 | -0,15924305 | -0,07868831 | 0,06250000 | нет | |
| 2,12500000 | 2,18750000 | 2,15625000 | 0,00119806 | -0,07868831 | -0,03866032 | 0,03125000 | нет | |
| 2,12500000 | 2,15625000 | 2,14062500 | 0,00119806 | -0,03866032 | -0,01870977 | 0,01562500 | нет | |
| 2,12500000 | 2,14062500 | 2,13281250 | 0,00119806 | -0,01870977 | -0,00875050 | 0,00781250 | нет | |
| 2,12500000 | 2,13281250 | 2,12890625 | 0,00119806 | -0,00875050 | -0,00377488 | 0,00390625 | нет | |
| 2,12500000 | 2,12890625 | 2,12695313 | 0,00119806 | -0,00377488 | -0,00128807 | 0,00195313 | нет | |
| 2,12500000 | 2,12695313 | 2,12597656 | 0,00119806 | -0,00128807 | -0,00004492 | 0,00097656 | нет | |
| 2,12500000 | 2,12597656 | 2,12548828 | 0,00119806 | -0,00004492 | 0,00057659 | 0,00048828 | нет | |
| 2,12548828 | 2,12597656 | 2,12573242 | 0,00057659 | -0,00004492 | 0,00026584 | 0,00024414 | нет | |
| 2,12573242 | 2,12597656 | 2,12585449 | 0,00026584 | -0,00004492 | 0,00011046 | 0,00012207 | нет | |
| 2,12585449 | 2,12597656 | 2,12591553 | 0,00011046 | -0,00004492 | 0,00003277 | 2,12591553 | 0,00006104 | да |
| 2,12591553 | 2,12597656 | 2,12594604 | 0,00003277 | -0,00004492 | -0,00000608 | 2,12594604 | 0,00003052 | да |
| 2,12591553 | 2,12594604 | 2,12593079 | 0,00003277 | -0,00000608 | 0,00001335 | 2,12593079 | 0,00001526 | да |
Приближенное решение 
, погрешность 
, число итераций 
. Следовательно, приближенное значение корня равно 
.
Задание 7. Найти корень нелинейного уравнения 
методом итерации с точностью 
.
Решение. Задачу будем решать по следующей схеме:
1) отделим корни.
2) приведем исходное уравнение к виду 
. Для этого заменим уравнение уравнением вида 
. Величину 
подберем так, чтобы для функции 
выполнялись условия теоремы о достаточном условии сходимости итерационного процесса.
Производная 
на отрезке 
отрицательна, следовательно, функция 
на этом отрезке монотонно убывает, как это показано на рис. 2.11.
Рис. 2.11 – Значения функции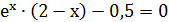 
на отрезке
Значения функции 
:
Учитывая монотонный характер функции и из последних равенств легко заметить, что условия теоремы о достаточном условии сходимости итерационного процесса заведомо выполнено, если – правильная отрицательная дробь (см. рис. 2.12).
|
|
|
Рис. 2.12 – Продолжение метода итраций. Определение значения
Так как производная на концах отрезка положительна (
и 
) и монотонно возрастает, ее модуль имемаксимум на правой стороке отрезка. Тогда если за принять число 
055, то для любого 
из отрезка значение выражения будет правильной отрицательной дробью. Это отбеспаечивет выполнение условия теоремы о достаточном условии сходимости итерационного процесса.
Для выполнения последнего условия теоремы найдем производную преобразованной функции
3)
Контрольные вопросы
1. Этапы решения уравнения с одной неизвестной.
2. Способы отделения корней.
3. Каким образом графическое отделение корней уточняется с помощью вычислений?
4. Дать словесное описание алгоритма метода половинного деления.
5. Необходимые условия сходимости метода половинного деления.
6. Условие окончания счета метода простой итерации. Погрешность метода.
7. Словесное описание алгоритма метода хорд. Графическое представление метода. Вычисление погрешности.
8. Словесное описание алгоритма метода касательных (Ньютона). Графическое представление метода. Условие выбора начальной точки.
Варианты заданий к лабораторной работе №3
Исходные данные к заданиям приведены в табл. 3.1
Задание 1: 1) Отделить корни уравнения графически и программно.
2) Уточнить корни (все!) уравнения методом половинного
деления с точностью .
Задание 2: 1) Отделить корни уравнения графически и программно.
2) Уточнить корни уравнения методом итерации с
точностью .
Задание 3: 1) Отделить корни уравнения графически и программно.
2) Уточнить корни уравнения методом хорд с
точностью .
Задание 4: 1) Отделить корни уравнения графически и программно.
2) Уточнить корни уравнения методом касательных с
точностью .
Таблица 3.1 – Исходные данные к лабораторной работе №3
| Вариант | Уравнение (метод половинного деления) | Уравнение (метод итераций) | Уравнение (метод хорд) | Уравнение (метод асательных) |
| 
| 
| 
| |
|
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
|
| |
| 
| 
|
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
|
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
|
|
|
|
|
|
|
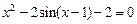
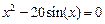
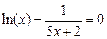
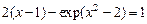
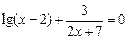
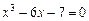
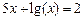
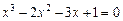
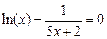
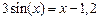
