 |
Кривые второго порядка в полярных координатах
|
|
|
|
ВВЕДЕНИЕ
Данное руководство представляет собой методические указания к выполнению лабораторной работы, в которую входят задачи по темам: “Кривые второго порядка”, “Кривые в полярной системе координат”, “Поверхности второго порядка”.
Перед заданиями лабораторной работы приведены основные положения теории, определения, формулы, подробно рассмотрены решения типовых задач.
При выполнении лабораторной работы необходимо привести формулы, с помощью которых решается задача, сделать подробные вычисления и необходимые пояснения к решению.
ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Линии второго порядка
Линия (кривая) второго порядка – это линия, определяемая уравнением второй степени относительно текущих координат x и y, т.е. уравнением вида:

| (1) |
При соответствующем выборе системы координат уравнение линии второго порядка можно привести к простейшему виду.
К линиям второго порядка относятся: эллипс, гипербола, парабола.
Эллипс. Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух данных точек (фокусов) есть величина постоянная (эта постоянная больше расстояния между фокусами).
Каноническое уравнение эллипса:
 , ,
| (2) |
где a =ОА - большая полуось,
b =ОВ - малая полуось.
Координаты фокусов: F 1(- c; 0), F 2(c;0), где c = 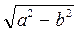 .
.

Эксцентриситетом эллипса называется отношение фокусного расстояния 2 с к большой полуоси 2 а:  (
( , так как с<a).
, так как с<a).
Директрисами эллипса называются прямые, уравнения которых  .
.
Расстояние точки М (х,y) эллипса до фокусов (фокальные радиусы) определяются формулами:
r1= 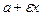 ; r2= ; r2=  . .
|
В частном случае a = b фокусы F 1 и F 2 совпадают с центром, а каноническое уравнение имеет вид:
|
|
|
 , или , или  , ,
|
т.е. описывает окружность радиуса  с центром в начале координат.
с центром в начале координат.
Гипербола. Гиперболой называется геометрическое место точек, разность расстояний от которых до двух данных точек (фокусов) есть величина постоянная (указанная разность берется по абсолютному значению; требуется также, чтобы она была меньше расстояния между фокусами и отлична от нуля).
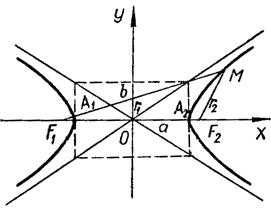
Каноническое уравнение гиперболы:
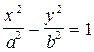 , ,
| (3) |
где а = ОА 1= ОА 2 – действительная полуось;
b - мнимая полуось.
Фокусы гиперболы: F 1(- c;0), F 2(c;0), где 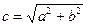 .
.
Эксцентриситетом гиперболы называется отношение  (
( >1, так как с > a).
>1, так как с > a).
Асимптоты гиперболы: y =  .
.
Расстояния точки М (х;y) гиперболы до ее фокусов определяется формулами: r1=  ; r2=
; r2=  .
.
Прямые х =  называются директрисами гиперболы.
называются директрисами гиперболы.
Гиперболы  и
и  называются сопряженными.
называются сопряженными.
Гипербола с равными полуосями (a=b) называется равносторонней, ее уравнение:

|
Парабола. Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы).
Уравнение параболы, симметричной относительно оси Ох и проходящей через начало координат, имеет вид:
 . .
| (4) |

Уравнение директрисы 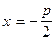 . Парабола имеет фокус F (
. Парабола имеет фокус F ( ).
).
Фокальный радиус точки М(х;y) параболы выражается формулой r =  .
.
Парабола, симметричная относительно оси Оy и проходящая через начало координат, имеет уравнение:

| (5) |
Уравнение директрисы этой параболы:  .
.
Фокус параболы: F (0;  ).
).
Фокальный радиус точки М (x;y) параболы: r =  .
.
Кривые второго порядка в полярных координатах
Полярными координатами точки М на плоскости называется полярный радиус  >0 и полярный угол
>0 и полярный угол  , отсчитываемый от полярной оси ОР котрезку ОМ против движения часовой стрелки (
, отсчитываемый от полярной оси ОР котрезку ОМ против движения часовой стрелки ( <0, если поворот осуществляется по часовой стрелке). Значение угла, удовлетворяющее условию 0
<0, если поворот осуществляется по часовой стрелке). Значение угла, удовлетворяющее условию 0  , называют главным значением.
, называют главным значением.

Прямоугольные декартовы координаты и полярные координаты точки М, при условии, что начало декартовой системы координат совпадает с полюсом, а положительное направление оси Ох декартовой системы координат совпадает с направлением полярной оси, связаны формулами:
|
|
|

| 
| |

| 
| (6) |
Уравнение линии на плоскости в полярных координатах:

| (7) |
Примеры некоторых кривых и их уравнений в полярных координатах:
r = 
| спираль Архимеда | (8) |
r = 
| гиперболическая спираль | (9) |
r = 
| логарифмическая спираль | (10) |

| лемниската Бернулли | (11) |
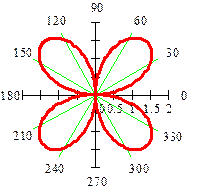
r = 
| четырехлепестковая роза | (12) |
r= 
| кардиоида | (13) |
r = 
| улитка Паскаля | (14) |
r = 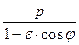
| эллипс, если  <1,
парабола, если <1,
парабола, если  =1,
гипербола, если =1,
гипербола, если  >1. >1.
| (15) |

| 
| |||
| Рисунок 1 – Спираль Архимеда | Рисунок 2 – Гиперболическая спираль | |||

| 
| |||
| Рисунок 3 – Логарифмическая спираль | Рисунок 4 – Лемниската Бернулли | |||
| 
| |||
| Рисунок 5 – Четырехлепестковая роза | Рисунок 6 – Кардиоида | |||

| ||||
| Рисунок 7 – Улитка Паскаля | ||||
Параметрические уравнения
Параметрическими уравнениями линии на плоскости называются уравнения вида: 

| (16) |
где 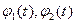 - функции переменной t.
- функции переменной t.
|
|
|


