Преобразования прямоугольных координат

Координаты (x;y) точки М в прямоугольной декартовой системе координат Оxy (старой) и ее координаты (X;Y) в другой прямоугольной системе О₁XY (новой) связаны формулами:

при параллельном переносе или

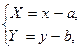
где (a; b) - координаты нового начала О₁ в старой системе координат;

при повороте осей вокруг начала координат на угол :

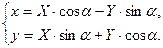
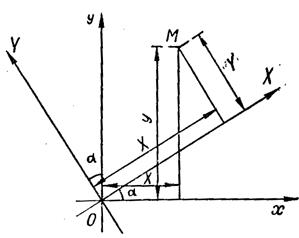
Уравнение вида (1) путем выделения полного квадрата и используя далее преобразования прямоугольных координат, о которых говорилось выше, можно привести к одному из видов (2)-(5).

Поверхности второго порядка

Поверхностью второго порядка называется поверхность, определяемая уравнениями второй степени относительно текущих координат x, y, z.

При соответствующем выборе прямоугольной декартовой системы координат в пространстве уравнение поверхности второго порядка можно привести к одному из видов:

		эллипсоид	(17)
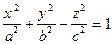
		однополостный гиперболоид	(18)
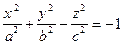
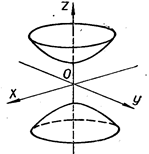
		двуполостный гиперболоид	(19)
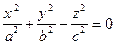
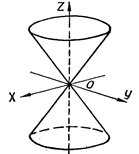
		конус	(20)
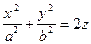
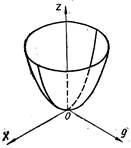
		эллиптический параболоид	(21)
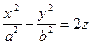
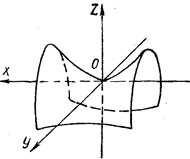
		гиперболический параболоид	(22)
		эллиптический цилиндр	(23)
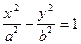
		гиперболический цилиндр	(24)
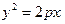
		параболический цилиндр	(25)
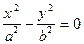
		пара пересекающихся плоскостей	(26)
		пара параллельных плоскостей	(27)
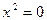
		пара совпадающих плоскостей	(28)
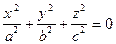
		мнимый конус	(29)
		пара мнимых пересекающихся плоскостей	(30)
		мнимый эллипсоид	(31)
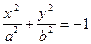
		мнимый эллиптический цилиндр	(32)
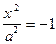
		пара мнимых параллельных плоскостей	(33)
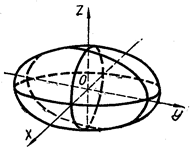
Рисунок 8 – Эллипсоид		Рисунок 9 – Однополостный гиперболоид
	Рисунок 10 – Двуполостный гиперболоид	Рисунок 11 – Конус
	Рисунок 12 – Эллиптический параболоид		Рисунок 13 – Гиперболический параболоид
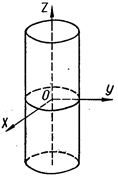
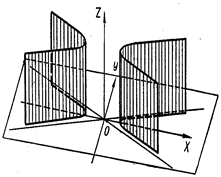
	Рисунок 14 – Эллиптический цилиндр		Рисунок 15 – Гиперболический цилиндр
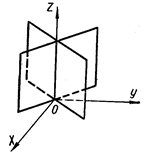
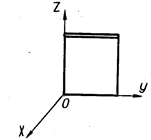
	Рисунок 16 – Параболический цилиндр		Рисунок 17 - Пара пересекающихся плоскостей
		.
	Рисунок 18 – Пара параллельных плоскостей		Рисунок 19 – Пара совпадающих плоскостей

ЗАДАНИЯ ДЛЯ ЛАБОРАТОРНОЙ РАБОТЫ

1.Записать каноническое уравнение и определить вид кривой. Записать уравнения директрис, асимптот (если это необходимо). Определить координаты фокусов, вершин, центров и другие параметры полученной кривой.

1.1	4x2+8x+y2-2y-11=0	1.2	x2+y2-4x+2y-4=0
1.3	9x2+4y2-24y=0	1.4	x2+4y2-6x+5=0
1.5	16x2+9y2-32x-36y-92=0	1.6	4x2+y2-8x-4y-8=0
1.7	x2+4y2-4x-32=0	1.8	x2+25y2+2x+100y-124=0
1.9	x2+4x+4y2-32=0	1.10	x2+y2+2x-4y-4=0
1.11	y2-x-2y+4=0	1.12	y2-6x-6y+21=0
1.13	x2-2x-y-5=0	1.14	x2-8x-8y+24=0
1.15	2y2-x-12y+14=0	1.16	y2+x-6=0
1.17	x+y2-2y-1=0	1.18	4x2-y-8x+7=0
1.19	9x2-y2+36x+45=0	1.20	4x2-25y2-8x-100y-196=0
1.21	9x2-4y2+18x+16y-43=0	1.22	x2-4y2-6x-24y-31=0
1.23	x2-4y2—2x+8y-19=0	1.24	4y2-x2+4x+12=0

 

1.25	-25x2+25y2—100x+100y-225=0	1.26	5x2+5y2-30x+20y+20=0
1.27	9x2-4y2+72x-16y+92=0	1.28	9x2-y2+36x=0
1.29	9x2-y2-54x-4y+41=0	1.30	9x2+y2+2y-35=0

2. Записать каноническое уравнение поверхности. Определить ее вид. Построить тело, ограниченное указанными поверхностями.

2.1	4x2-y2+2z2-16x+12=0, y=0, y=3	2.2	9x2-2y2+4z2+18x-8z+49=0, y=6
2.3	9x2+4y2-z2-18x-16y+61=0, z=12	2.4	2x2+8y2-8z=0, z=4
2.5	4x2+y2-z2+16x+12=0, z=0, z=2	2.6	4x2+9y2-36z2+8x+144z-176=0, z=3, z=0
2.7	4x2+9y2-36z2+8x+144z-176=0, y=0, y=2	2.8	x2-9y2-2x-z+1=0, z=3
2.9	9x2-16y2+9z2+144=0, y=0	2.10	4x2+9y2-z2+36=0, z=12
2.11	9x2+16y2+9z2-144=0, x=0, x=2	2.12	9x2+9y2+36z2-72z=0, z=1, z=2
2.13	x2+9y2-2x-8=0, z=y, y=0	2.14	-4x2+9y2+z2+36=0, x=8
2.15	9x2+4y2-z2-2x-16y-11=0, x=2, x=1	2.16	4x2+9y2-36z2-24x=0, z=0, z=4
2.17	2x2-8y2-z=0, z=4	2.18	-4x2+16y2+z2-32y=0, x=0, x=2
2.19	x2+4y2+6x-8y-4z+13=0, z=4	2.20	x2+y2+z2-36=0, x=0, x=2
2.21	2x2+18y2-z=0, z=18	2.22	4x2+16y2+z2-32y=0, z=-2, z=2
2.23	4x2+16y2+z2+32y=0, z=0, z=3	2.24	4x2+9y2+8x+36y-z2+4=0, z=0, z=4
2.25	16x2-9y2+9z2=0, y=0, y=3	2.26	9x2+25y2-225z2-225=0, z=0, z=2
2.27	y2-4x2+16z2=0, x=0, x=2	2.28	9x2+y2-18x=0, z=4, z=1
2.29	4x2+9y2-z2-8x-36y+4=0, z=0, z=2	2.30	4x2-4y2-4z2-16x-32=0 z=0, z=3

ОБРАЗЦЫ ВЫПОЛНЕНИЯ ЗАДАНИЙ

Пример 1

Записать каноническое уравнение и определить вид кривой, заданной уравнением:

.

 

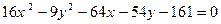Определить основные параметры кривой. Изобразить кривую на плоскости.

Решение:

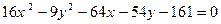
Преобразуем левую часть уравнения, выделяя полный квадрат:

,

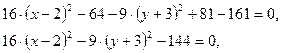
16 (x-2)²-9 (y+3)²=144.

Разделим обе части уравнения на 144:

-это каноническое уравнение гиперболы со смещенным центром. Координаты центра О₁(2;-3).

Осуществим параллельный перенос системы координат Оxy: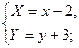

тогда в новой системе координат О₁XY уравнение гиперболы будет иметь вид:

.

Действительная ось этой гиперболы - ось О₁X, мнимая ось - ось О₁Y, фокусы лежат на оси О₁X.

Определим параметры гиперболы:

а) полуоси гиперболы ;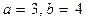

б) межфокальное расстояние ;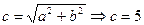

в) координаты фокусов в новой системе координат O₁XY: F₁ =(5;0), F₂ =(-5;0),

в старой системе координат Oxy: F₁=(7;-3), F₂=(-3;-3);

г) эксцентриситет ;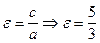

д) уравнение асимптот в новой системе координат: ,

в старой системе координат: ,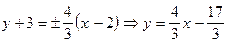

;

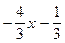е) уравнение директрис в новой системе координат: ,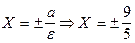

в старой системе координат: ,

и ;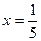

ж) строим график

Литература: [5], стр. 44-59; [8], стр. 52-81; [9], стр. 82-89.

Пример 2

Записать каноническое уравнение поверхности. Определить ее вид. Построить тело, ограниченное указанными поверхностями:

а)	, z=-6, z=6;
б)	, x=8, x=-8.

 

Решение:

а)

;

.

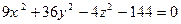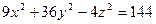Разделим обе части уравнения на 144

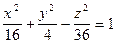. (1)

Это уравнение однополостного гиперболоида с полуосями a =4, b =2, c =6.

Однополостный гиперболоид симметричен относительно координатных плоскостей, координатных осей, начала координат, т.к. если в уравнении (1) заменить х на (-х), y на (-y), z на (-z), то уравнение не изменится.

Найдем сечения гиперболоида координатными плоскостями (главные сечения):

1) плоскостью Оxy: 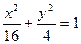- сечение плоскостью Оxy есть эллипс с полуосями a=4,b=2 и центром в О(0;0;0)

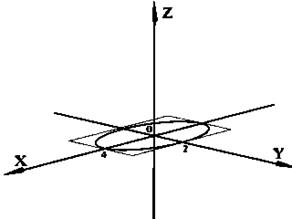
2) плоскостью Oxz: 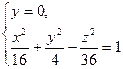- сечение плоскостью Oxz есть гипербола с действительной осью Оx и мнимой осью Оz, полуоси a=4,c=6.

 

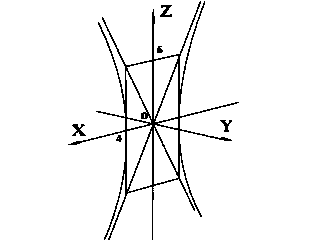
3) плоскостью Оyz: 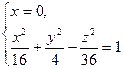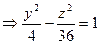- сечение плоскостью Оyz есть гипербола с действительной осью Оy и мнимой осью Оz, полуоси b=2, c=6.

 

 

 

 

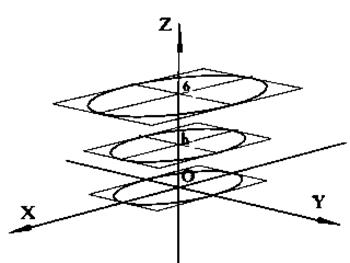
Найдем сечения гиперболоида плоскостями, параллельными координатным плоскостям:

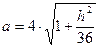1) плоскостью, параллельной плоскости Оxy: - сечение есть эллипс с полуосями и .

При уменьшении h полуоси эллипса уменьшаются, при увеличении h - увеличиваются.

В частности при 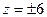получаем сечение плоскостями параллельными оси Оxy:

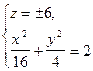- эллипс с полуосям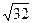и и .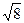

 

 

 

 

2) плоскостью, параллельной плоскости Оxz: 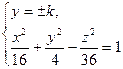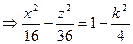- очевидно, что при 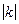<2 сечение есть гипербола с действительной осью Оx, а при 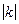> 2 сечение будет гиперболой с действительной осью Оz, при сечение представляет собой пару прямых, пересекающихся в точке (0;2;0) или (0;-2;0);

3) аналогично пункту 2).

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: