 |
Парная линейная регрессия.
|
|
|
|
МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ.
| Между двумя переменными существует статистическая связь, если при изменении значения одной переменной меняется распределение другой. |
Для двух количественных переменных наиболее часто используется модель линейной связи 
. Если между двумя переменными существует линейная связь, то при увеличении значения переменной 
значение переменной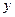 
пропорционально увеличивается (прямая, положительная связь) или уменьшается (обратная, отрицательная связь).
Определить, существует ли связь между переменными и является ли она линейной, прямой или обратной, проще всего по диаграмме рассеяния.
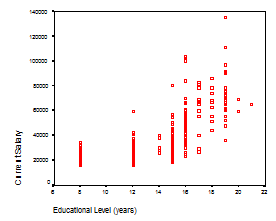
Линейная связь является полной, если все точки на диаграмме рассеяния лежат на прямой ; сильной или тесной, если облако точек достаточно прилегает к прямой достаточно близко; слабой, если облако точек по отношению к прямой широко разбросано.
Теснота (сила) линейной связи измеряется с помощью коэффициента линейной корреляции Пирсона 
где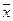 
– среднее арифметическое для переменной ,
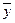– среднее арифметическое для переменной ,
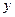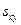– ковариация переменных и ,
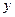– среднее квадратическое отклонение для переменной ,
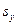– среднее квадратическое отклонение для переменной .
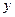Коэффициент Пирсона обладает следующими свойствами:
;
, если между переменными нет связи, или если связь не является линейной;
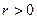, если линейная связь является прямой (положительной);
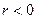, если линейная связь является обратной (отрицательной);
при этом чем ближе значение 
к +1 или к –1, тем теснее связь;
, если связь является полной.
Для сгруппированных переменных коэффициент Пирсона вычисляется по таблице сопряженности.
|
|
|
Большинство методов многомерной статистики предназначено для анализа структуры связей между несколькими переменными. Наиболее полно она описывается матрицей корреляций, в клетках которой указываются значения коэффициентов корреляции для соответствующих переменных. Матрица корреляций симметрична относительно главной диагонали, которая полностью состоит из единиц (коэффициент корреляции переменной самой с собой равен 1).
Для коэффициента корреляции может проверяться гипотеза о статистической значимости.
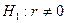
| Выборочное значение коэффициента является статистически значимым, если по нему можно заключить, что значение коэффициента для генеральной совокупности будет отличаться от нуля |
Для проверки гипотезы выбранный уровень значимости (
) необходимо сравнить с напечатанным в клетке таблицы значением Sig. (two-tailed).
Если 
, коэффициент корреляции статистически значим (на уровне значимости 
); между переменными существует линейная связь.
Если 
, наличие линейной статистической связи подтвердить не удалось (не исключено, что связь есть, но она не является линейной).
Различают корреляционные и причинные статистические связи. Корреляционная связь не имеет причинной компоненты; для ее измерения достаточно коэффициента корреляции, в который обе переменные входят абсолютно симметрично.
Парная линейная регрессия.
Причинная связь предполагает, что одна из переменных (называемая независимой) измеряет причину, а вторая переменная (называемая зависимой) – следствие. Уравнение является статистической моделью причинной линейной связи и называется уравнением регрессии. Независимая переменная обозначена в нем буквой , зависимая – буквой 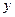. С помощью уравнения регрессии можно предсказать, каким будет среднее значение зависимой переменной 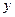при определенном значении независимой переменной .
|
|
|
Коэффициент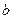 
называется коэффициентом регрессии и вычисляется по формуле
,
где – среднее квадратическое отклонение для переменной ,
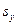– среднее квадратическое отклонение для переменной .
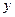Знак коэффициента регрессии совпадает со знаком коэффициента корреляции. Равенство значения коэффициента нулю свидетельствует об отсутствии линейной связи.
Коэффициент регрессии показывает, насколько, в среднем, увеличится или уменьшится значение зависимой переменной 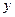при увеличении значения независимой переменной на 1.
Коэффициент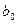 
называется свободным членом уравнения регрессии и вычисляется по формуле 
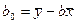; во многих задачах он не интерпретируется.
При повышении уровня образования на 1 год зарплата, в среднем, увеличивается, на $3,910.
Для параметров регресси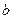и и 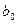проверяются гипотезы о статистической значимости по тому же алгоритму, что и для коэффициента корреляции.
Качество уравнения парной регрессии, его объясняющая способность измеряется коэффициентом детерминации 
. Коэффициент детерминации показывает, какая доля дисперсии (изменчивости) зависимой переменной 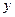объясняется влиянием независимой переменной .
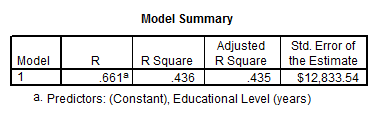
Интерпретация: 44% всех различий в зарплате объясняется образованием.
|
|
|
