 |
Множественная линейная регрессия.
|
|
|
|
В большинстве задач следствие не может быть объяснено одной единственной причиной; как правило, приходится изучать влияние на него нескольких причин одновременно. Для исследования такой множественной связи используется уравнение множественной линейной регрессии: 
или, более коротко 
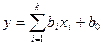, где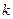 
– количество независимых переменных, используемых в анализе:
По уравнению множественной регрессии можно предсказать, каким будет среднее значение зависимой переменной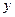 
при определенных значениях независимых переменных 
.
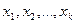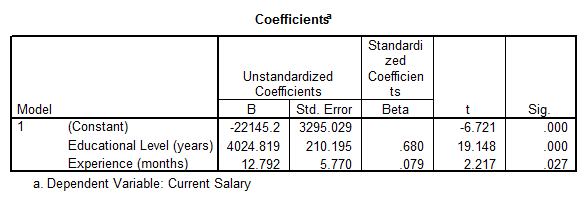
Например: при образовании 16 лет и опыте работы 24 месяца средняя зарплата составляет 
$
Уравнение множественной регрессии может быть представлено как в нестандартизированном (коэффициенты B), так и в стандартизированном виде (коэффициенты Beta). Стандартизированные коэффициенты показывают величину относительного "вклада" зависимых переменных в изменение независимой переменной.
Например: образование влияет на доход почти в 10 раз сильнее, чем стаж работы.
Для определения качества модели множественной линейной регрессии используется квадрат коэффициента множественной корреляции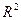 
, измеряющий тесноту связи между зависимой переменной 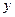и набором независимых переменных 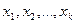. 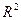является аналогом коэффициента детерминации 
и интерпретируется как доля изменчивости зависимой переменной 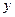, объясняемая совокупным влиянием набора независимых переменных .
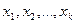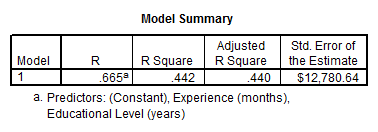
Независимые переменные, включенные в одну модель, могут взаимодействовать между собой и опосредовать влияние друг друга на зависимую переменную. Поэтому лучшей считается модель, в которую в качестве независимых переменных включены все показатели, оказывающие влияние на зависимую переменную.
|
|
|
Использование дихотомических переменных в регрессионном анализе.
Регрессионный анализ изначально предназначался для количественных переменных, однако в последнее время активно развиваются техники, позволяющие включать в регрессионные модели номинальные переменные. Наиболее часто используются дихотомические переменные.
Еслидихотомическая переменная используется в качестве зависимой переменной 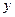, уравнение регрессии будет предсказывать вероятность события, закодированного значением 1.
Если дихотомическая переменная является независимой переменной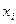 
, коэффициент регрессии для нее показывает, насколько изменится среднее значение 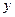при изменении значения 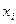с 0 на 1.
Вычисление уравнения множественной регрессии.
Уравнение множественной регрессии строится в два этапа.
1. Вычисляются коэффициенты стандартизированного уравнения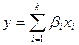 
. Для их нахождения необходимо решить систему линейных уравнений:
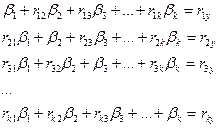
2. Коэффициенты нестандартизированного уравнения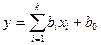 
вычисляются по формулам:
, 
,
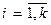
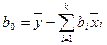где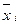 
– среднее арифметическое для переменной ,
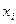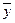– среднее арифметическое для переменной ,
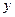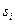– среднее квадратическое отклонение для переменной 
,
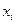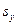– среднее квадратическое отклонение для переменной .
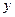Вычисление коэффициента множественной корреляции.
,
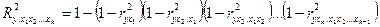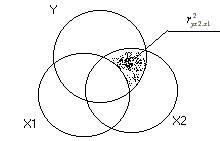
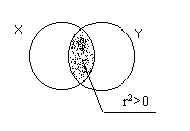
где 
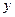– коэффициент корреляции между переменными и 
,
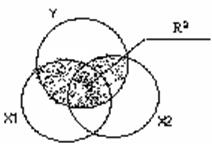
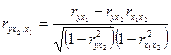– частный коэффициент корреляции между переменным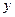и и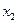 
при устраненном влиянии переменной ,
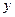– частный коэффициент корреляции между переменными и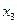 
при устраненном влиянии переменных и ,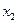
 |  | ||
и т.п.
 |  | ||
SPSS
Построение диаграммы рассеяния:
Graphs ½ Scatter… ½ Simple ½ Define ½поместить имена двух переменных в окошки X Axis и Y Axis ½ OK
Вычисление коэффициента Пирсона:
|
|
|
Analyze ½ Correlate ½ Bivariate ½поместить имена переменных в окно Variables ½ Correlation coefficient: выбрать Pearson ½ Test of significance: выбрать Two-tailed ½отметить Flag significant correlations ½ OK
Построение уравнения множественной линейной регрессии:
Analyze ½ Regression ½ Linear… ½поместить имя зависимой переменной в окно Dependent ½поместить имена независимых переменных в окно Independent(s) ½ Method: enter½ OK
|
|
|
