 |
Методика оценивания знаний и накопления баллов
|
|
|
|
Утверждаю
декан морского факультета
_____________ С. П. Голиков
«______» ____________ 2012 г.
РАБОЧАЯ ПРОГРАММА учебной дисциплины
ВЫСШАЯ МАТЕМАТИКА
для специальности «Судовождение»
по направлению 6.070104 «Морской и речной транспорт»
образовательно-квалификационный уровень – бакалавр
| Форма обучения | Нормативные данные | |||||||||
| Курс | Семестр | Всего часов / кредитов ECTS | Лекции, часов | Лабораторные работы, часов | Практические занятия, часов | Всего аудиторных часов | Самостоятельная работа, часов | курсовой проект (работа), часов/ кредитов ЕСТS | Семестровый контроль | |
| дневная | 162/4,5 | -- | -- | экзамен | ||||||
| 108/3 | экзамен | |||||||||
| Итого | 270/7,5 |
Рабочая программа составлена на основании типовой программы дисциплины и рабочего учебного плана с учетом требований ОПП
Программу разработала Егорова С.Н., старший преподаватель кафедры ВМиФ КГМТУ
Рассмотрено на заседании кафедры высшей математики и физики КГМТУ
Протокол № ___ от _________ 2012 г. Зав. кафедрой ВМиФ ____________Т.Н. Попова
Рассмотрено на заседании выпускающей кафедры «Судовождение» КГМТУ
Протокол № ___ от _________ 2012 г. Зав. кафедрой ОПРП ____________ Г.И. Пазынич
Согласовано учебной частью _____________________________ _________________ 2012г.
Цель и задачи изучения дисциплины, ее место в учебном процессе
Учебная дисциплина «Высшая математика» является фундаментальной дисциплиной, которая обеспечивает базовую подготовку судоводителя. Она предназначается для обеспечения студента знаниями и навыками, необходимыми для изучения общеинженерных и профилирующих дисциплин. Содержание дисциплины в значительной мере определяет уровень общенаучной подготовки судоводителя.
|
|
|
Дисциплина имеет цель:
- выработать у студентов навыки в математическом исследовании различных технологических проблем;
- развить логическое мышление, пространственное воображение;
- овладеть основными методами высшей математики и реализацией их на ЭВМ;
- приобрести умение самостоятельно расширять математические знания и производить математический анализ прикладных задач.
Основные задачи курса:
- повысить уровень фундаментальной подготовки;
- усилить прикладную направленность курса математики к требованиям специальности.
Курс высшей математики является базой для изучения таких общеобразовательных и специальных курсов как:
- физика;
- теоретическая механика;
- сопротивление материалов;
- компьютерная техника;
- математические основы судовождения;
- математическая статистика в судовождении и др.
Требования к знаниям, умениям и навыкам студента
В результате изучения курса «Высшая математика» студент должен в 1-м семестре
ЗНАТЬ:
Понятия определителя, матрицы. Схему исследования СЛАУ. Геометрические системы координат на плоскости и в пространстве. Элементы векторной алгебры. Основные задачи аналитической геометрии на плоскости и в пространстве. Кривые и поверхности второго порядка. Теорию пределов. Производные и их применение. Построение графиков функций. Понятие функции двух переменных, частных производных, градиента.
УМЕТЬ:
Вычислять определители. Решать системы линейных алгебраических уравнений тремя способами. Уметь применять скалярное, векторное и смешанное произведения векторов для решения задач геометрии, механики, физики. Решать задачи аналитической геометрии на плоскости и в пространстве. Проводить прямую и обратную линейную интерполяцию. Различать и строить кривые и поверхности второго порядка по их каноническому и общему уравнениям. Дифференцировать функции и строить их графики. Решать задачи оптимизации. Использовать дифференциал функции в приближённых вычислениях. Проводить обработку результатов наблюдений методом наименьших квадратов.
|
|
|
В результате изучения курса «Высшая математика во 2-м семестре студент должен
ЗНАТЬ: Понятие и свойства неопределенного интеграла. Методы интегрирования рациональных, тригонометрических и некоторых иррациональных функций. Задачи, приводящие к понятию определенного интеграла. Формулу Ньютона-Лейбница. Несобственные интегралы 1-го и 2-го рода. Методы вычисление площади криволинейной трапеции, объёма и поверхности тела. Классификацию дифференциальных уравнений 1-го (с разделяющимися переменными, однородные и линейные) и 2-го порядка (допускающие понижение порядка, линейные однородные и неоднородные уравнения с постоянными коэффициентами) и методы их решения.
УМЕТЬ: Находить неопределенные интегралы, применяя методы непосредственного интегрирования, замены переменной, интегрирования по частям. Вычислять определенные интегралы, пользуясь формулой Ньютона-Лейбница. Вычислять площади криволинейных трапеций, объёмы и поверхности тел. Решать дифференциальные уравнения 1-го порядка (с разделяющимися переменными, однородные и линейные). Решать линейные однородные и неоднородные уравнения 2-го порядка. Описывать технические и природные процессы с помощью дифференциальных уравнений.
Структура дисциплины
Дисциплина «Высшая математика» в первом семестре содержит 1 зачетный кредит, который состоит из двух зачетных модулей.
| Тема | Общее кол-во часов | Кол-во аудит. часов | Часов по видам занятий | ||||||
| Лекции | Лаб. работы | Практич. занятия | Самост. работа | ||||||
| Зачетный кредит 1 | |||||||||
| Зачетный модуль 1 | |||||||||
| Содержательный модуль 1 «Элементы линейной алгебры» Понятие и методы вычисления определителей. Матрицы. Действия с матрицами. Понятие СЛАУ. Исследование и решение систем уравнений методами Крамера, матричным, Гаусса. | -- | ||||||||
| Содержательный модуль 2«Элементы векторной алгебры» Понятие вектора. Геометрические и аналитические действия над векторами. Скалярное, векторное, смешанное произведение векторов. | -- | ||||||||
| Содержательный модуль 3 «Элементы аналитической геометрии» Системы координат на плоскости и в пространстве. Простейшие задачи. Различные уравнения прямой на плоскости, в пр-ве и плоскости в пр-ве. Взаимное расположение прямых и плоскостей. Линейные неравенства. Понятие линейной интерполяции. Кривые и поверхности второго порядка. | -- | ||||||||
| Модульный контроль 1: контрольная работа (10 баллов) | |||||||||
| Зачетный модуль 2 | |||||||||
| Содержательный модуль 4 «Введение в анализ» Понятие функции. Основные элементарные функции. Свойства. Преобразования графиков. Предел последовательности, предел функции. Бесконечно большие и бесконечно малые величины. Первый и второй замечательные пределы. Непрерывность функций. Точки разрыва. | -- | ||||||||
| Содержательный модуль 5 «Элементы дифференциального исчисления функции одной переменной» Понятие производной функции. Производные различных функций. Дифференциал функции, производные высших порядков. Некоторые теоремы о дифференцируемых функциях. Исследование поведения функций и построение графиков. | -- | ||||||||
| Модульный контроль 2: контрольная работа (10 баллов) | |||||||||
| Всего часов | -- | ||||||||
| Семестровый контроль (50 баллов) | |||||||||
Дисциплина «Высшая математика» во втором семестре содержит 1 зачетный кредит, который состоит из двух зачетных модулей.
|
|
|
| Тема | Общее кол-во часов | Кол-во аудит. часов | Часов по видам занятий | ||||||
| Лекции | Лаб. работы | Практич. занятия | Самост работа | ||||||
| Зачетный кредит 2 | |||||||||
| Зачетный модуль 1 | |||||||||
| Содержательный модуль 6 «Функции нескольких переменных» Функции нескольких переменных. Частные производные. Оценка погрешности с помощью дифференциала. Градиент. Метод наименьших квадратов. | -- | ||||||||
| Содержательный модуль 7 «Комплексные числа. Многочлены» Понятие комплексного числа. Действия с комплексными числами. Алгебраическая, тригонометрическая, показательная формы комплексного числа. Разложение многочлена на множители. | -- | ||||||||
| Содержательный модуль 8 «Неопределённый интеграл» Понятие неопределенного интеграла. Табличные интегралы. Основные методы интегрирования разных классов элементарных функций. | -- | ||||||||
| Модульный контроль 1: контрольная работа (10 баллов) | |||||||||
| Зачетный модуль 2 | |||||||||
| Содержательный модуль 9 «Определенный интеграл» Определенный интеграл. Основные свойства. Формула Ньютона-Лейбница. Несобственные интегралы. | -- | ||||||||
| Содержательный модуль 10 «Приложения определенного интеграла» Вычисление площадей, объемов тел вращения, длины дуги кривой. Физические приложения определенного интеграла. | -- | ||||||||
| Содержательный модуль 11 «Дифференциальные уравнения» Дифференциальные уравнения 1-го порядка (с разделяющимися переменными, однородные и линейные). Уравнения 2-го порядка, допускающие понижение порядка. Линейные однородные и неоднородные уравнения 2-го порядка с постоянными коэффициентами. Дифференциальные уравнения механических колебаний. | -- | ||||||||
| Модульный контроль 2: контрольная работа (10 баллов) | |||||||||
| Всего часов | |||||||||
| Семестровый контроль (50 баллов) | |||||||||
|
|
|
Содержание лекций
| Семестр | Nсодерж. модуля | № лекции | Объем (час) | Наименование тем, краткое содержание материала. |
| Понятие СЛАУ. Решение СЛАУ размера 2Х2. Введение понятия определителя 2-го порядка. Формулы Крамера. | ||||
| Решение СЛАУ размера3Х3. Введение понятия определителя 3-го порядка. Свойства определителей, методы их вычисления. | ||||
| Понятие матрицы. Виды матриц. Действия над матрицами. Алгоритм нахождения обратной матрицы. | ||||
| Решение СЛАУ матричным методом и методом Гаусса. Понятие ранга матрицы. Общая схема исследования СЛАУ. | ||||
| 5-7 | Понятие вектора. Геометрические и аналитические действия над векторами. Скалярное, векторное, смешанное произведение векторов. Их физические и геометрические применения. | |||
| Системы координат на плоскости и в пространстве. Простейшие задачи (расстояние между двумя точками, деление отрезка в заданном отношении, площадь треугольника). | ||||
| Уравнение линии на плоскости (поверхности в пространстве). Уравнение прямой с угловым коэффициентом; общее уравнение прямой (плоскости); Уравнение прямой, проходящей через данную точку. Уравнение прямой (плоскости) в отрезках на осях. Уравнение прямой, проходящей через две заданные точки. Расстояние от точки до прямой. | ||||
| Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых. Взаимное расположение двух прямых на плоскости. Геометрический смысл линейных неравенств. Понятие линейной интерполяции в задачах судовождения. | ||||
| 10, | Кривые второго порядка. Канонические уравнения окружности, эллипса, гиперболы, параболы. Исследование формы. Практические приложения. Преобразование координат. Приведение общего уравнения линии 2-го порядка к каноническому виду. | |||
| Поверхности второго порядка (сфера, эллипсоид, гиперболоиды, параболоиды, цилиндрические, конические, вращения). | ||||
| Постоянные и переменные величины. Понятие функциональной зависимости. Основные элементарные функции. Свойства. Преобразования графиков. | ||||
| Числовые последовательности и их пределы. Предел функции. | ||||
| Бесконечно большие и бесконечно малые величины. Первый замечательный предел. Эквивалентные бесконечно малые функции. Второй замечательный предел. Раскрытие различных видов неопределённостей. | ||||
| Непрерывность функции. Точки разрыва и их классификация. | ||||
| Производная и ее геометрический и физический смысл. Производная суммы, произведения, частного. | ||||
| 18,19 | Производные элементарных функций. Производная сложной и обратной функции. Таблица производных. Производные неявных и параметрически заданных функций. Логарифмическое дифференцирование. | |||
| Дифференциал функции и его свойства. Применение в приближённых вычислениях. Производные высших порядков. | ||||
| Теорема Ферма, Роля, Лагранжа и Коши. Правило Лопиталя и его использования при вычислении пределов функций. | ||||
| 22,23 | Возрастание и убывание функций. Нахождение экстремумов функций и асимптот. Выпуклость и вогнутость кривых. Точки перегиба. | |||
| Исследование поведения функций и построение графиков. | ||||
| 25,26 | Функции нескольких переменных. Частные производные Геометрический смысл полного дифференциала функций двух переменных. Оценка погрешности с помощью дифференциала. Производная по направлению. Градиент. Экстремумы функций двух переменных. Задачи оптимизации. | |||
| Получение функции на основании экспериментальных данных по методу наименьших квадратов. | ||||
| 28,29 | Понятие комплексного числа. Алгебраическая, тригонометрическая и показательная формы комплексных чисел. Действия над комплексными числами. | |||
| Многочлен. Корни многочлена. Разложение многочлена на множители в случае действительных и комплексных корней. | ||||
| 31,32 | Понятие первообразной функции и неопределенного интеграла. Его свойства. Табличные интегралы. Метод непосредственного интегрирования. | |||
| Метод интегрирования подстановкой (заменой переменной). Метод интегрирования по частям. | ||||
| Интегрирование рациональных функций. Метод неопределенных коэффициентов. | ||||
| 35,36 | Интегрирование тригонометрических и некоторых иррациональных функций. | |||
| Понятие определенного интеграла и его свойства. Формула Ньютона-Лейбница. | ||||
| Замена переменной в определенном интеграле. Интегрирование по частям. Интегрирование четных и нечетных функций в симметричных пределах. | ||||
| Несобственные интегралы 1-го и 2-го рода. | ||||
| 40-42 | Геометрические приложения определенного интеграла. Физические приложения определенного интеграла. | |||
| Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения 1-го порядка. Задача Коши. | ||||
| Уравнения с разделяющимися переменными. Однородные уравнения. | ||||
| Линейные дифференциальные уравнения 1-го порядка. Уравнения Бернулли. | ||||
| Дифференциальные уравнения высших порядков. Дифференциальные уравнения 2-го порядка допускающие понижения порядка. | ||||
| 47,48 | Линейные однородные уравнения 2-го порядка с постоянными коэффициентами. Характеристические уравнения. Неоднородные уравнения 2-го порядка с постоянными коэффициентами. Структура общего решения ЛНДУ 2-го порядка | |||
| Дифференциальные уравнения механических колебаний. |
Темы практических занятий
|
|
|
| Семестр | N содерж. модуля | № занятия | Объем (час) | Наименование тем, краткое содержание материала |
| Определители второго и третьего порядка. Их свойства и методы вычисления. | ||||
| Матрицы, их сложение и перемножение. Обратная матрица и способы ее вычисления. | ||||
| 3,4 | Исследование и решение неоднородных и однородных систем алгебраических уравнений с помощью формул Крамера, методом Гаусса, матричным способом. | |||
| 5-7 | Линейные операции над векторами в геометрической форме. Нахождение координат, длины, направления вектора. Вычисление скалярного, векторного, смешанного произведения векторов через их проекции на координатные оси и непосредственно. Задачи на геометрическое и физическое приложения произведений векторов. | |||
| Нахождение расстояния между двумя точками на плоскости. Деление отрезка в заданном отношении. Составление уравнения линии как ГМТ. Построение прямой по различным её уравнениям. | ||||
| Решение задач на нахождение элементов треугольника с использованием уравнения прямой, проходящей через данную точку в заданном направлении, уравнение прямой, проходящей через две заданные точки, формулы угла между двумя прямыми. Задание треугольника системой линейных неравенств. | ||||
| Задачи на нахождение элементов кривых 2-го порядка и их построение по каноническим уравнениям. Исследование общего уравнения линии 2-го порядка. | ||||
| Приведение общего уравнения линии 2-го порядка к каноническому виду с помощью параллельного переноса осей системы координат. Построение кривой. | ||||
| Модульная контрольная работа. | ||||
| Нахождение области определения функции, её характерных свойств. Построение графиков путём элементарных преобразований. | ||||
Предел последовательности, предел функции. Раскрытие неопределенностей 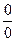 , ,  . .
| ||||
| Раскрытие других видов неопределенностей. Первый замечательный предел. Эквивалентные бесконечно малые величины. | ||||
| Второй замечательный предел. Задачи на классификацию точек разрыва. | ||||
| 17- | Производная элементарных функций. Правила нахождения производных. Нахождение производных сложных функций. | |||
| Нахождение производных неявных и параметрически заданных функций. Производные высших порядков. | ||||
| Нахождение дифференциала функции. Использование правила Лопиталя при вычислении пределов функций. | ||||
| Нахождение экстремумов функций. Наибольшее, наименьшее значение функции на отрезке. Задачи оптимизации. | ||||
| Задачи на определение критических точек 2-го рода. Выпуклость, вогнутость функции. Асимптоты. | ||||
| Исследование и построение графиков функций с помощью производных | ||||
| Модульная контрольная работа. | ||||
| Функции двух переменных. Частные производные. Геометрический смысл полного дифференциала функций двух переменных. Оценка погрешности с помощью дифференциала. Производная по направлению. Градиент. | ||||
| Экстремумы функций двух переменных. Задачи оптимизации. | ||||
| Получение функции на основании экспериментальных данных по методу наименьших квадратов. | ||||
| Комплексные числа. Действия с комплексными числами в различной форме (алгебраической, тригонометрической, показательной). | ||||
| Многочлен. Корни многочлена. Разложение многочлена на множители в случае действительных и комплексных корней. | ||||
| Табличные неопределенные интегралы. Непосредственное интегрирование. | ||||
| Интегрирование методом замены переменной. | ||||
| Метод интегрирования по частям. | ||||
| Интегрирование простейших рациональных дробей 4-х типов. Разложение правильной рациональной дроби на простейшие с использованием метода неопределенных коэффициентов. | ||||
| Интегрирование тригонометрических функций | ||||
| Интегрирование иррациональных функций. | ||||
| Модульная контрольная работа. | ||||
| Формула Ньютона-Лейбница Замена переменной в определенном интеграле. Интегрирование по частям. | ||||
| Интегралы с бесконечными границами и от разрывных функций. | ||||
| 39-41 | Геометрические приложения определённого интеграла (вычисление площадей, объёмов тел, длины дуги кривой). Физические приложения определенного интеграла. | |||
| 42,43 | Решение дифференциальных уравнений 1-го порядка с разделяющимися переменными и однородных. Задача Коши. | |||
| Линейные уравнения 1-го порядка и уравнения Бернулли. Решение методом Бернулли и Лагранжа. | ||||
| Решение дифференциальных уравнений 2-го порядка, допускающих понижение порядка. | ||||
| 46,47 | Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и специальной правой частью. | |||
| Модульная контрольная работа. |
Содержание и объем самостоятельной и индивидуальной работы студента
Самостоятельная работа включает часы, необходимые студенту на подготовку к плановым аудиторным контрольным и самостоятельным работам, а также на исследование некоторых вопросов теории.
Семестр
| Содержательный модуль | Часы | Литература | Содержание работы |
| 1. Элементы линейной алгебры. | [1] гл. 5 §1-5 [2] гл. 1§5, гл. 4 §§1;5;6 [5] с. 124-138 [6] с. 86-190 [7] с. 194-207; [8] гл. 13 | Изучить лекционный материал. Освоить вычисление определителей третьего порядка, решение СЛАУ тремя методами. | |
| 2. Элементы векторной алгебры. | [1] гл. 1 §1; 3 [2] гл. 2 [5] с. 139-158 [7] гл. 7 [8] гл. 14 | Изучить лекционный материал. Овладеть линейными операциями над векторами. Понять формулы для вычисления скалярного, векторного, смешанного произведений векторов, их физический и геометрический смысл. | |
| 3. Элементы аналитической геометрии. | [1] гл. 1 §2, гл. 2; 3 [2] гл. 1 §§1-4, гл. 3 [5] с. 8-123, 159-211 [7] гл. 1-6, 8-9 [8] гл. 1-4, 14 | Проработать лекционный материал по данной теме. Выучить основные формулы. Научиться решать задачи по нахождению элементов в треугольнике на плоскости, приводить к каноническому виду уравнения кривых 2-го порядка и строить их, производить прямую и обратную линейную интерполяцию. | |
| 4. Введение в анализ. | [2] гл. 6 [4] гл. 1 [5] с. 212-357 [7] гл. 5-6 [9] гл. 1-2 | Выучить определения предела, свойства конечных пределов. Освоить методы раскрытия неопределенностей. Понять определение односторонних пределов и непрерывности функции в точке и освоить классификацию точек разрыва. | |
| 5. Элементы дифференциального исчисления функции одной переменной. | [2] гл. 7 §§1- 2 [4] гл. 2 §§1-13, гл. 3 [5] с. 358-497 [6] гл 1 с.186-253 [7] гл. 7-8 [9] гл. 3-5 | Выучить определение производной, ее свойства, таблицу основных производных. Научиться вычислять производную сложной функции. Понять физический и геометрический смысл производной и дифференциала. Научиться применять дифференциал в приближённых вычислениях. Изучить и освоить общую схему исследования функции и построения графика с помощью производных. | |
| Итого |
Семестр
| Содержательный модуль | Часы | Литература | Содержание работы |
| 6. Функции нескольких переменных. | [2] гл. 8 §§1-2; 4 [4] гл. 6 [5] с. 499-574 [8] гл. 15 [9] гл. 8 | Научиться находить эмпирическую функцию методом наименьших квадратов. | |
| 7. Комплексные числа. Многочлены. | [1] гл. 5 §6 [6] с. 5-60 [9] гл. 7 | Знать, какие числа являются комплексными. Научиться выполнять действия с комплексными числами в различной форме. | |
| 8. Неопределенный интеграл. | [2] гл. 9 [4] гл. 4 [5] с. 575-715 [7] гл. 9 [9] гл. 10 | Выучить определение первообразной и неопределенного интеграла, их свойства, таблицу основных интегралов. Научиться различать основные методы интегрирования. | |
| 9. Определенный интеграл. | [2] гл. 10 §§1-2 [4] гл. 5§§1-2 [5] с. 716-769 [7] гл. 10 §§54-57 [9] гл. 11 | Выучить формулу Ньютона-Лейбница, формулу интегрирования по частям определенных интегралов. Знать алгоритм вычисления несобственных интегралов. | |
| 10. Приложения определенного интеграла. | [2] гл. 10 §§3-10 [4] гл. 5 §§3-11 [5] с. 777-811 [7] гл. 10 §§58-59 [9] гл. 12 | Разобрать идею решения физических задач с помощью интегралов. | |
| 11. Дифференциальные уравнения. | [3] гл. 4 §§1-3 [4] гл. 9 §§1-10 [5] с. 812-941 [8] гл. 16 [9] гл. 13 | Научиться определять тип уравнения и предлагать способ его решения. Пытаться давать механическую интерпретацию линейных уравнений 2-го порядка с постоянными коэффициентами. | |
| Итого |
Методы и формы обучения
В соответствии с «Положением об организации учебного процесса в высших учебных заведениях» основными формами изучения дисциплины являются: чтение лекций, проведение практических занятий и самостоятельная работа студентов.
Лекции проводятся в лекционных аудиториях в соответствии с рабочим учебным планом специальности «Судовождение». Практические занятия посвящены, в основном, решению задач. При этом происходит закрепление теоретического материала и получение практических навыков его использования. Кроме того, студентам предлагаются задания как чисто прикладного содержания согласно специфике специальности, так и теоретического характера для более глубокого освоения фундаментальных основ предмета.
В I семестре модульный контроль осуществляется путем выполнения аудиторных контрольных работ (зачетные модули 1, 2).
Во II семестре модульный контроль осуществляется путем выполнения аудиторных контрольных работ (зачетные модули 1, 2).
Методика оценивания знаний и накопления баллов
І семестр
1. Посещение лекций, наличие и качество конспекта – до 0,25 балла за лекцию (максимум 6 баллов)
2. Оценка практических навыков (посещение, активность, успешность на п/з – до 0,25 балла за занятие, самостоятельная работа – до 18 баллов) - максимум 24 баллов
3. модульный контроль (2 контрольных работы, каждая из которых состоит из оценки за практическую часть –8 баллов, теоретическую часть –2 балла) – максимум 20 баллов
4. Экзамен - 50 баллов
Итого 100 баллов
IІ семестр
1. Посещение лекций, наличие и качество конспекта – до 0,25 балла за лекцию (максимум 6 баллов)
2. Оценка практических навыков (посещение, активность, успешность на п/з – до 0,25 балла за занятие, самостоятельная работа – до 18 баллов) - максимум 24 баллов
3. модульный контроль (2 контрольных работы, каждая из которых состоит из оценки за практическую часть –8 баллов, теоретическую часть –2 балла) – максимум 20 баллов
4. Экзамен - 50 баллов
Итого 100 баллов
|
|
|


