 |
Перечень вопросов, которые выносятся на семестровый контроль
|
|
|
|
⇐ ПредыдущаяСтр 2 из 2
(I семестр)
- Определители 2-го и 3-го порядков, их вычисление и свойства.
- Минор, алгебраическое дополнение элемента. Вычисление определителя разложением по элементам ряда. Понятие об определителях произвольного порядка.
- Понятие матрицы. Виды матриц. Линейные операции над матрицами. Умножение матриц.
- Матрица, обратная данной. Алгоритм её нахождения.
- Понятие о системах m линейных алгебраических уравнений с n неизвестными. Общая схема исследования.
- Понятие о ранге матрицы. Методы его вычисления. Условие совместности СЛАУ.
- Решение системы линейных алгебраических уравнений с помощью формул Крамера.
- Решение системы линейных алгебраических уравнений средствами матричного исчисления.
- Элементарные преобразования. Метод Гаусса решения СЛАУ.
- Основные и свободные неизвестные. Решение СЛАУ для случая m = n.
- Исследование однородных систем линейных уравнений.
- Векторы на плоскости и в пространстве. Коллинеарные и компланарные вектора. Линейные операции над векторами (в геометрической форме).
- Линейная зависимость и независимость векторов. Понятие базиса. Разложение вектора по базису.
- Проекция вектора на ось. Теоремы о проекциях.
- Системы координат на плоскости и в пространстве. Базисы на плоскости и в пространстве. Координаты вектора и точки. Длина и направление вектора.
- Линейные операции над векторами в координатной форме. Условие коллинеарности векторов.
- Скалярное произведение 2-х векторов. Формулы для вычисления, свойства, геометрические и физические приложения. Условие перпендикулярности двух векторов.
- Векторное произведение 2-х векторов. Формулы для вычисления, свойства, геометрические и физические приложения. Условие коллинеарности двух векторов.
- Смешанное произведение 3-х векторов. Формулы для вычисления, свойства, геометрический смысл. Условие компланарности трёх векторов.
- Различные системы координат на плоскости (в пространстве). Связь между ними.
- Простейшие задачи аналитической геометрии на плоскости и в пространстве (расстояние между двумя точками, деление отрезка в данном отношении).
- Задание множеств точек уравнениями и неравенствами. Алгоритм составления уравнения линии. Примеры.
- Общее уравнение прямой на плоскости. Его исследование.
- Уравнение прямой с угловым коэффициентом. Его исследование.
- Уравнение прямой, проходящей через две точки. Уравнение прямой в отрезках.
- Уравнение прямой, проходящей через данную точку. Расстояние от точки до прямой.
- Угол между двумя прямыми на плоскости. Условия параллельности, перпендикулярности.
- Взаимное расположение 2-х прямых на плоскости.
- Уравнение плоскости в пространстве (в отрезках, через 3 точки). Расстояние от точки до плоскости.
- Понятии линейной интерполяции.
- Общее уравнение кривой 2-го порядка. Окружность. Каноническое уравнение. Исследование формы.
- Каноническое уравнение эллипса и его основные соотношения.
- Гипербола. Каноническое уравнение. Исследование формы.
- Парабола. Каноническое уравнение. Исследование формы.
- Преобразование координат. Приведение уравнений кривых 2-го порядка к каноническому виду в простейших случаях.
- Основные применения кривых 2-го порядка.
- Простейшие поверхности 2-го порядка.
- Понятие множества. Виды числовых множеств. Окрестность точки.
- Функция. Способы задания. Основные свойства. Область определения.
- Основные элементарные функции. Элементарные функции и их классификация.
- Построение графика функции путём элементарных преобразований.
- Последовательность и ее предел.
- Предел функции. Бесконечно большие и бесконечно малые величины.
- Основные теоремы о конечных пределах.
- Первый замечательный предел.
- Бесконечно большие функции и их свойства. Связь между б.м. и б.б. функциями.
- Второй замечательный предел.
- Понятие о неопределённых выражениях. Основные методы раскрытия неопределённостей.
- Непрерывность функции в точке. Свойства непрерывных функций.
- Производная, ее геометрический и механический смыл.
- Производная суммы, произведения и частного двух функций.
- Производные элементарных функций.
- Производные сложных, неявных и параметрически заданных функций.
- Производные обратных функций. Логарифмическое дифференцирование.
- Дифференциал и его свойства. Применение в приближённых значениях.
- Производные и дифференциалы высших порядков.
- Основные теоремы дифференциального исчисления (Ферма, Роля, Лагранжа).
- Правило Лопиталя.
- Признаки возрастания и убывания функции в интервале. Экстремум функции. Необходимое условие экстремума.
- Первое и второе достаточные условия экстремума.
- Отыскание наибольшего и наименьшего значений функции на отрезке и интервале.
- Выпуклость и вогнутость кривых. Точки перегиба.
- Асимптоты графика функции.
- Исследование графиков функций.
|
|
|
|
|
|
(II семестр)
- Понятие о функции нескольких переменных.
- Полное и частное приращение функции.
- Частные производные функций нескольких переменных.
- Полный дифференциал.
- Касательная плоскость и нормаль к поверхности.
- Частные производные и дифференциалы высших порядков.
- Необходимый признак экстремума функций двух переменных.
- Нахождение функции на основании экспериментальных данных по методу наименьших квадратов.
- Понятие комплексного числа.
- Геометрическое изображение комплексного числа.
- Сложение и вычитание комплексных чисел.
- Умножение и деление комплексных чисел.
- Тригонометрическая и показательная форма комплексного числа.
- Возведение в степень и извлечение корня из комплексного числа.
- Первообразная функция. Основные теоремы о первообразных.
- Понятие неопределенного интеграла.
- Теорема о производной от неопределенного интеграла.
- Теорема о дифференциале от неопределенного интеграла.
- Теорема о неопределенном интеграле от дифференциала.
- Доказать, что постоянный множитель можно выносить за знак неопределенного интеграла.
- Теорема о неопределенном интеграле от алгебраической суммы конечного числа функций.
- Метод замены переменной (внесение под знак дифференциала).
- Интегрирование по частям неопределенного интеграла.
- Схема разложения алгебраических дробей на элементарные.
- Интегралы вида
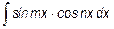 ;
;  ;
;  .
. - Интегралы вида
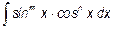 (m>0, n>0, хотя бы одно из них нечетное).
(m>0, n>0, хотя бы одно из них нечетное). - Интегралы виды
 ;
;  (m – нечетное).
(m – нечетное). - Интегралы вида
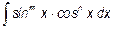 (m>0, n>0, оба четные).
(m>0, n>0, оба четные). - Интегралы вида
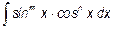 (m>0, n<0, оба четные);
(m>0, n<0, оба четные); 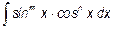 (m и n нечетные, одно из них отрицательное);
(m и n нечетные, одно из них отрицательное); 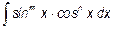 (m и n отрицательные, их сумма четное число).
(m и n отрицательные, их сумма четное число). - Интегралы вида
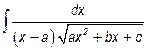 .
. - Интегрирование иррациональных выражений с помощью тригонометрических подстановок.
- Интегральная сумма и ее свойства.
- Понятие определенного интеграла.
- Геометрический смысл определенного интеграла.
- Свойства определенного интеграла.
- Теорема о среднем для определенного интеграла.
- Формула Ньютона-Лейбница.
- Замена переменной в определенном интеграле.
- Интегрирование по частям определенного интеграла.
- Интегралы с бесконечными пределами интегрирования.
- Интегралы от разрывных функций.
- Вычисление площадей в декартовых координатах.
- Вычисление площадей, ограниченных кривыми, заданными параметрически.
- Площадь криволинейного сектора в полярных координатах.
- Вычисление объема тела по известным площадям параллельных сечений.
- Вычисление объема тела вращения.
- Длина дуги кривой в декартовых координатах.
- Длина дуги кривой, заданной параметрически.
- Длина дуги кривой в полярных координатах.
- Частные и общие решения дифференциального уравнения 1-го порядка.
- Дифференциальные уравнения с разделяющимися переменными.
- Однородные уравнения.
- Линейные уравнения.
- Уравнения Бернулли.
- Частные и общие решения дифференциального уравнения 2-го порядка.
- Дифференциальные уравнения вида
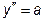 ,
,  .
. - Дифференциальные уравнения вида
 ;
;  .
. - Дифференциальные уравнения вида
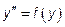 ;
;  .
. - Основная теорема об общем решении линейного однородного уравнения 2-го порядка.
- В каком случае
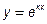 является решением линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами.
является решением линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами. - Вид общего решения линейного дифференциального уравнения второго порядка в случае, если корни характеристического уравнения действительные и различные.
- Вид общего решения линейного однородного дифференциального уравнения 2-го порядка, если корни характеристического уравнения кратные.
- Вид общего решения линейного однородного дифференциального уравнения 2-го порядка, если корни характеристического уравнения комплексные.
- Теорема об общем решении линейного неоднородного дифференциального уравнения 2-го порядка.
- Метод Лагранжа решения неоднородного линейного дифференциального уравнения 2-го порядка.
- Дифференциальные уравнения малых колебаний механических систем.
|
|
|
|
|
|
12. Методическое обеспечение и рекомендуемая литература
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры./ Д.В. Беклемишев – М.: Наука, 1974. – 320 с.
2. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 –х ч. Ч. I: Учеб. пособие для втузов./ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова – М.: Высшая школа, 1997.– 304 с.
3. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 –х ч. Ч. II: Учеб. пособие для втузов./ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова – М.: Высшая школа, 1997.– 416 с.
4. Запорожец Г.И. Руководство к решению задач по математическому анализу./ Г.И. Запорожец – М.: Высшая школа, 1966. – 460 с.
- Каплан И.А. Практические занятия по высшей математике. Ч. 1 – 3. / И.А. Каплан – Харьков: Изд-во ХГУ, 1967. – 946 с.
- Каплан И.А. Практические занятия по высшей математике. Ч. 5. / И.А. Каплан – Харьков: Изд-во ХГУ, 1967. –378 с.
- Клетеник Д.В.Сборник задач по аналитической геометрии: учеб. пособие для втузов. /Д.В. Клетеник – СПб.: Изд-во «Профессия», 2003. – 200 с.
- Слободская В.А. Краткий курс высшей математики: учеб. пособие для втузов./ В.А. Слободская – М.: Высшая школа, 1969. – 544 с.
- Пискунов Н.С. Дифференциальное и интегральное исчисления: учеб. пособие для втузов./ Н.С. Пискунов – М.: Физматгиз, 1962. – 856 с.
|
|
|
Воспользуйтесь поиском по сайту:

©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...

