 |
Определение весомости параметров
|
|
|
|
Определение весомости параметров
Коэффициент весомости определяется экспертным путем, т. е. путем опроса экспертов или потенциальных покупателей. Для расчета коэффициента весомости каждого показателя (КВ) проводится опрос. Для заполнения анкеты используется метод предпочтений, когда наиболее важным признакам присваивается цифра 1, далее 2, 3 и т. д. (столбец 2 таблицы 3. 6). Далее определяется ранг, то есть место, которое занимает показатель, по мнению эксперта (столбец 3 таблицы 3. 6). И заключительным этапом рассчитаем весомости показателей (B) для первого эксперта по формуле (3. 6) и результат занесем в последний столбец таблицы 3. 6.
 ,
| (3. 6) |
где Bi – весомость оцениваемого параметра;
n – количество сравниваемых параметров;
Pi – ранг.
Таблица 3. 6 – Расчет весомостей по мнения первого эксперта
| № параметра | Номер показателя по важности | Ранг, Pi | Весомость, Bi |
| 5, 5 | 2, 5 | ||
| 5, 5 | 2, 5 | ||
Оценки весомости показателей каждого из экспертов заносятся в итоговую таблицу 3. 7. В таблице выполнен расчет коэффициента весомости (КBi), который показывает, какую долю занимает каждый показатель в общей совокупности.
Таблица 3. 7 – Результаты расчета коэффициента весомости, квадрата отклонения и коэффициента одинаковых повторений
| № пар-ра | Эксперты | Сумма весомостей, Вij | Коэф-т весомости, КBi | ||||||
| 5, 5 | 33, 5 | 0, 2393 | |||||||
| 5, 5 | 4, 5 | 23, 0 | 0, 1643 | ||||||
| 3, 5 | 2, 5 | 13, 0 | 0, 0929 | ||||||
| 2, 5 | 2, 5 | 11, 0 | 0, 0786 | ||||||
| 2, 5 | 5, 5 | 2, 5 | 12, 5 | 0, 0893 | |||||
| 3, 5 | 4, 5 | 21, 0 | 0, 1500 | ||||||
| 2, 5
| 5, 5 | 26, 0 | 0, 1857 | ||||||
| Итого | 140, 0 | 1, 00 | |||||||
Определение степени согласованности мнений экспертов
Разработанные коэффициенты весомости в таблице 3. 7 можно использовать в практических расчетах, если мнения экспертов являются согласованными. Согласованность экспертов определяется с помощью коэффициента конкордации.
Коэффициент конкордации определяется по формуле:
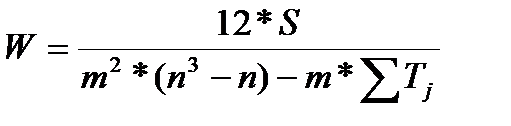, (3. 7)
где m – количество экспертов;
n – количество факторов, подлежащих оценке;
Tj – показатель связанных рангов.
Квадрат отклонения (S) рассчитывается по формуле:
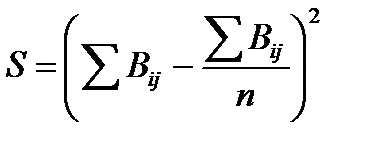(3. 8)
Количество одинаковых рангов, назначенных экспертами j-му признаку, по формуле:
, (3. 9)
где h - количество одинаковых повторений.
Коэффициент может принимать значения в пределах от 0 до 1. При полной согласованности мнений экспертов коэффициент конкордации равен единице при полном разногласии – нулю. Наиболее реальным является случай частичной согласованности мнений экспертов.
По мере увеличения согласованности мнений экспертов коэффициент конкордации возрастает и в пределе стремится к единице. Однако даже если он равен или близок к нулю, не всегда имеет место полное разногласие. Среди экспертов могут быть группы с хорошо согласованными мнениями, но мнения эти – противоположны и в общей массе нейтрализуют друг друга. В таком случае следует проделать кластерный или комбинированный анализ для выявления этих групп.
Расчет квадрата отклонения и количества одинаковых рангов представлен в таблице 3. 8
|
|
|
Таблица 3. 8 – Результаты расчета коэффициента весомости, квадрата отклонения и коэффициента одинаковых повторений
| № пар-ра | Эксперты | Сумма весомостей, Вij | Коэф-т весомости, КBi | Квадрат отклонения, S | ||||
| 5, 5 | 33, 5 | 0, 2393 | 182, 25 | |||||
| 5, 5 | 4, 5 | 23, 0 | 0, 1643 | 9, 00 | ||||
| 3, 5 | 2, 5 | 13, 0 | 0, 0929 | 49, 00 | ||||
| 2, 5 | 2, 5 | 11, 0 | 0, 0786 | 81, 00 | ||||
| 2, 5 | 5, 5 | 2, 5 | 12, 5 | 0, 0893 | 56, 25 | |||
| 3, 5 | 4, 5 | 21, 0 | 0, 1500 | 1, 00 | ||||
| 2, 5 | 5, 5 | 26, 0 | 0, 1857 | 36, 00 | ||||
| Итого | 140, 0 | 1, 00 | 414, 5 | |||||
| Tij | ||||||||
Определим согласованность мнений экспертов по формуле (3. 7):
С целью определения вероятности степени согласованности мнений экспертов, рассчитывается критерий Пирсона.
Вывод о значимости коэффициента конкордации делается в том случае, если выполняется условие:
Расчетное значение 
определяется по формуле:
(3. 10)
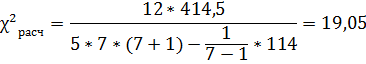
По специальной таблице определяем значение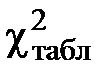 
в зависимости от заданной вероятности и числа степеней свободы. Число степеней свободы равно количеству сравниваемых объектов минус 1.
h = m - 1
h = m – 1= 7 – 1 = 6,
C вероятностью равной 99% по таблице находим 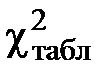=16, 8
Таким образом, можно сделать вывод, что , т. е. условие выполняется.
Это значит, что с вероятностью 99% можно утверждать, что мнения экспертов согласованные и согласованность составляет 64%. Принимается гипотеза о достаточном согласии и достоверности экспертных оценок.
Анализ коэффициентов весомости позволяет сделать следующие выводы:
1) наиболее важный показатель по мнению экспертов – цена;
2) второе и третье место по важности занимают показатели: отчет по корректировкам и предупреждениям и доступ к приложению с любого компьютера, имеющего выход в сеть интернет - (6) и (7). Но (6) и (7) показателей нет в БИТ. Стандарт, 1С: Консолидация 8 и 1С: УПП 8. Таким образом, у авторского приложения формируется два существенных конкурентных преимущества.
|
|
|
