 |
Сходимость и сумма числового ряда
|
|
|
|
Введение
Сравнение ряд критерий математический
В данной работе рассмотрены следующие источники:
Архипов Г. И. Лекции по математическому анализу. - М.: Высш. шк., 1999, 347-366с.
Фихтенгольц Г. М. Курс дифференциального исчисления. Том 2. - М.: Лань,2002,11-32c.
Запорожец Г. И. Руководство к решению задач по математическому анализу. - М.: Высш. шк. 1966. 342с.
Харди Г. Х. Курс чистой математики. - М.: Гос. изд. иностр. лит.1949. 341 с.
Кудрявцев Л. Д. Курс математического анализа. Том 2. - М.: Высш. шк.,1988.25-27с.
В первом источнике подробно расписана вся тема, но нет определения знакопеременных рядов и геометрического смысла интегрального признака. Во втором источнике можно найти основные теоремы и определения, а также определение знакопеременного ряда и геометрический смысл интегрального признака, которые и представлены в работе. Геометрический смысл можно найти в пятом источнике, но в нем скудно раскрыты аспекты рассматриваемой темы. Третий источник дает лишь поверхностное представление о числовых рядах, рассматривая основные определения и теоремы. В четвертом источнике очень мало можно найти нужной информации, но можно рассмотреть признак сравнения рядов.
Исходя из анализа представленной литературы, основой для написания работы я посчитала целесообразнее использовать материал из первого источника, так как в нем более подробно и удобнее изложен материал.
Сходимость и сумма числового ряда
Определение 1. 
Пусть { 
} - произвольная числовая последовательность. Числовым рядом или просто рядом называется формальная бесконечная сумма S вида
.
Обычно используется следующая сокращенная запись:
,
|
|
|
Или просто 
.
Рассмотрим новую последовательность { 
}, задаваемое равенством
.
Определение 2. Последовательность { } называется последовательностью частичных (или частных) сумм ряда , а ее n-й член называется n-й частичной суммой этого ряда.
Определение 3. Если последовательностью { } частичных сумм ряда сходится к числу 
, т.е. если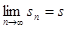 
, то ряд называется сходящимися (к ), а число - его суммой. В это случае пишут
.
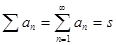Если же последовательность { } не имеет предела, то говорят, что ряд расходиться.
В основном нас будут интересовать сходящиеся ряды.
Определение 4. Если ряд сходится к числу , то последовательность 
называется остаточным членом или остатком ряда.
Заметим, что так как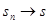 
при 
, то 
при .
Несколько модифицируем введенные определения и обозначения. Если в числовой последовательности { } отбросить несколько начальных членов, например, в количестве 
, то оставшиеся члены 
в совокупности можно снова рассматривать как некую новую последовательность { 
}, задаваемую равенством 
.
Рассматривая { } как общий член ряда 
для его частичных сумм 
получим равенство
.
Кроме того, ряд как формальную бесконечную сумму можно записать в виде
.
Таким образом, бесконечную сумму 
тоже можно рассматривать как ряд [1], [2], [3], [5].
Далее будем рассматривать также формальные ряды вида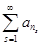 
, где ns - какая-либо последовательность натуральных чисел, и исследовать их на сходимость.
Утверждение 1. Остаточный член rn ряда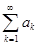 
можно представить в виде ряда 
в том смысле, что:
. его сумма равна rn, когда исходный ряд 
сходится
. это представление принимается как формальное равенство, когда оба равенства расходятся;
. другие случаи не имеют места.
Доказательство начнем с п.3. При 
для частичных сумм ряда и sk+n ряда имеет место равенство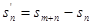 
.
Ясно, что при фиксированном n сходимость и расходимость последовательностей { } и {sk+n } имеют место одновременно, что и означает справедливость утверждения п.3.
|
|
|
В случае 1, т.е. когда оба ряда сходятся, можно перейти к пределу при 
в равенстве 
. Тогда получим
;
тем самым утверждение п. 1 доказано [1].
Относительно утверждения п. 2 следует заметить, что формальное равенство
Можно рассматривать как определение одной из возможных операций над формальными числовыми рядами. Приведении подобных операций необходимо только требовать, чтобы правые и левые части равенств переходили бы в равенство между числами в случае наличия сходимости хотя бы для одной из частей равенства, что действительно имеет место в нашем случае. Доказательство закончено.
Утверждение 2. Отбрасывание любого конечного числа членов в бесконечной сумме или прибавление к ней любого конечного числа новых слагаемых не влияет на сходимость ряда.
Доказательство. Рассмотрим случай отбрасывания слагаемых, так как второй случай разбирается аналогично. Итак, пусть мы отбросили члены ряда с номерами 
. Оставшиеся слагаемые переномеруем в порядке возрастания их прежних номеров. Общий член получившейся таким образом последовательности обозначим 
. Тогда при любом 
имеем
.
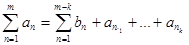Отсюда следует, что последовательности частичных сумм этих рядов 
и 
сходятся и расходятся одновременно. Утверждение доказано.[1].
Утверждение 3. Если 
и 
, то 
Утверждение 4. Если и 
, то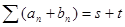 
.
Доказательство утверждений 3 и 4 есть прямое следствие определения суммы ряда и арифметических свойств сходящихся последовательностей { 
} и { 
} как частичных сумм рядов и 
. Доказательство закончено.
Утверждение 5. (необходимый признак сходимости ряда). Если ряд 
сходится, то 
при 
. Другими словами, { 
} есть бесконечно малая последовательность.
Доказательство. Имеем 
. Отсюда при получим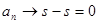 
, что и требовалось доказать.[1], [2], [5].
Примеры.
. Ряд 
сходится, и его сумма равна 1.
Действительно, имеем
при , т.е. 
.[1].
. Сумма членов бесконечной геометрической прогрессии вида
, при 
.
В случае 
имеем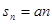 
, и ряд расходится. При 
справедливо равенство
.
Известно, что 
при 
и { 
} расходится при 
.
Таким образом, указанный ряд сходится к сумме 
при и расходится при 
, .[1].
|
|
|
.Гармонический ряд 
расходится, а ряд 
сходится при 
.
Применим теорему 2. При всех 
и 
имеем
.
Таким образом условия теоремы 2 будут выполнены, если положить 
и при любом 
в качестве и 
взять числа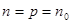 
. Тем самым расходимость ряда установлена. Для доказательства сходимости ряда 
по теореме Вейерштрасса достаточно доказать ограниченность его частичных сумм 
, поскольку они монотонно возрастают. Рассмотрим какое-либо 
с условием 
. Тогда справедлива следующая оценка
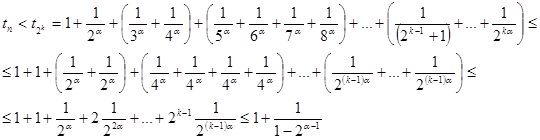
Таким образом, частичные суммы { 
} ограничены в совокупности, что и означает сходимость искомого ряда.[1].
Критерий Коши
Теорема 1 (критерий Коши). Для сходимости ряда 
необходимо и достаточно, чтобы для любого 
существовал номер 
такой, что при всяком натуральном и всех 
имело место равенство
.
Доказательство. Утверждение теоремы равносильно критерию Коши для сходимости { 
} частичных сумм ряда, что согласно определению и есть сходимость его самого. Теорема доказана.[1], [2], [5].
Теорему 1 можно переформулировать таким образом, чтобы иметь критерий расходимости ряда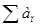 
в прямом виде.
Теорема 2 (критерий Коши для расходимости ряда). Для расходимости ряда 
необходимо и достаточно, чтобы существовало хотя бы одно 
с условием, что для любого номер найдутся натуральные 
и 
, для которых справедливо равенство
.[1].
Знакопостоянные ряды
Определение 5. Всякое выражение вида 
называется отрезком ряда.[1].
Определение 6. Знакопеременными называются ряды, члены которых имеют то положительный, то отрицательный знаки[2].
Определение 7. Ряд называется рядом с неотрицательными членами, если при всех n имеем 
.[1], [2].
Теорема 2. Для сходимости ряда 
, где при всех n, необходима и достаточна ограниченность последовательности его частичных сумм.
Доказательство. Пусть 
- n-я частичная сумма ряда . Поскольку 
, имеем, что { } не убывает. Теперь требуемый результат вытекает из критерия Вейерштрасса для сходимости монотонной последовательности. Доказательство закончено.[1].
|
|
|
Пример. Пусть 
и 
не убывает и положительна. Тогда ряд 
расходится, а ряд 
сходится.
Действительно, для частичных сумм и 
этих рядов имеем
[1].
Сравнение рядов
Теорема 3 (признак сравнения). Пусть и 
- два ряда с неотрицательными членами и пусть, начиная с некоторого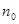 
, для всех 
имеем 
. Тогда:
. сходимость ряда влечет за собой сходимость ряда 
;
. из расходимости ряда следует расходимость ряда .
Доказательство. Без нарушения сходимости можно отбросить первые 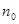членов каждого ряда. При всех полагаем
.
Тогда для любого имеем 
. В случае 1. последовательность { 
} ограничена, следовательно, и { 
} тоже ограничена и ряд сходится. В случае 2. последовательность 
, поэтому 
, т. е. ряд расходится. Теорема доказана.[1], [4], [5].
Замечание. Говорят, что ряд мажорирует ряд , а последний, в свою очередь, его минорирует.
Теорема 4 (обобщенный признак сравнения). Если в условии теоремы 3 неравенство 
заменить неравенством 
, то ее утверждение также будет иметь место.
Доказательств. Поскольку отбрасывание нескольких первых членов ряда не влияет на его сходимость, с самого начала можно считать, что 
. Перемножая все неравенства из условия теоремы до номера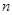 
включительно, приходим к неравенствам вида
, 
.
Применяя теорему 3, получаем требуемый результат относительно рядов 
и 
, а так как умножение всех членов ряда на одно и то же число, отличное от нуля, не влияет на сходимость, теорема доказана.[1].
|
|
|
