 |
Признаки сходимости Даламбера, Коши, интегральный признак сходимости
|
|
|
|
Теорема 5 (признак Даламбера). Пусть для членов ряда 
,начиная с некоторого номера 
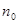, выполнены условия:
. 
;
. 
, где 
.
Тогда ряд 
сходится. Если же при всех 
вместо неравенства 2 имеем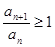 
, то ряд 
расходится.
Доказательство. Сравним ряд со сходящимся рядом 
, где 
. При имеем
.
Поэтому первое утверждение теоремы 5 вытекает из теоремы 4.
Во втором случае надо положить 
для всех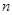 
. Тогда ввиду расходимости ряда 
и неравенств
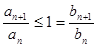
из той же теоремы 4 следует расходимость ряда 
. Теорема доказана.[1], [2], [5].
Теорема 6 (признак Даламбера в предельной форме). Рассмотрим ряд 
с условием 
для всех 
. Положим
, 
.
Тогда при всех 
ряд сходится, а при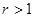 
- расходится.
Доказательство. Рассмотрим сначала первый случай. Положим 
. Тогда 
. Поскольку , при некотором 
имеем
.
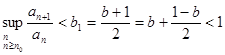Следовательно, ряд 
сходится в силу первого утверждения теоремы 5.
Рассмотрим теперь второй случай. Положим 
. Тогда имеем 
. Поскольку , при некотором 
имеем оценку
.
Тем самым ряд расходится по второму утверждению теоремы 5. Теорема доказана. [1].
Замечание. При 
вопрос о сходимости ряда в теоремах 5 и 6 остается открытым. Для примера можно указать на ряды 
и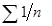 
, один из которых сходится, а другой - расходится, но в обоих случаях имеем . Для исследования сходимости подобных рядов требуются более «тонкие» признаки, которые будут рассмотрены позже.
Несколько тонкий признак дает следующая теорема.
Теорема 7 (признак Коши). Если для членов ряда с условием 
, начиная с некоторого номера , имеет место неравенство 
, где число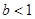 
и фиксировано, то ряд сходится.
Если же для бесконечно многих имеем 
, то этот ряд расходится.
|
|
|
Доказательство. Рассмотрим сначала первый случай. Последовательно имеем , 
, и так как 
, то ряд сходится по признаку сравнения вместе с рядом 
.
Во втором случае для бесконечного количества значений имеем , 
. Это значит, что 
и ряд расходится, поскольку условие необходимого признака сходимости ряда (
при 
) не выполняется. Теорема доказана.[1], [2], [5].
Теорема 8 (признак Коши в предельной форме). Пусть
,
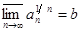где 
при всех .
Тогда при ряд сходится, а при 
- расходится.
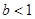Доказательство. Положим сначала и допустим, что . Тогда при некотором 
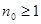имеем
.
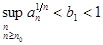Поэтому по первому случаю признака Коши ряд сходится.
Если же , то при всех 
имеем оценку
.
Это означает существование бесконечного множества значений , для которых справедливо неравенство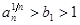 
. Следовательно, ряд расходится по второму случаю признака Коши. Теорема доказана.[1].
Признак Коши, как и признак Даламбера, является довольно грубым. Он, например, тоже не позволят решить вопрос о сходимости рядов 
и 
.
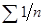Теорема 9 (интегральный признак Коши - Маклорена). Пусть функция 
определена на промежутке 
и убывает на нем. Тогда:
. если 
при всех 
и несобственный интеграл 
сходится, то ряд тоже сходится;
. если 
при всех и несобственный интеграл 
расходится, то расходится и ряд .
Доказательство. Как и выше, без ограничения общности будем считать, что 
. Далее, поскольку монотонно убывает, при всяком натуральном 
и 
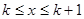имеем
.
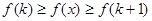Интегрируя это неравенство по указанному промежутку, получим
.
При всяком 
просуммируем эти неравенства по 
от 1 до 
. Получим
.
Далее каждый из двух случаев будем рассматривать отдельно.
. В этом случае интеграл 
сходится, поэтому при всех для частичных сумм 
ряда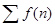 
имеет место единообразная оценка вида 
, и поскольку 
для всех натуральных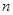 
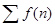, ряд сходится, а вместе с ним сходится и мажорируемый им ряд , что и требовалось доказать.
|
|
|
. Поскольку в этом случае интеграл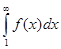 
расходится, 
при . Но так как
,
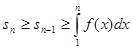то 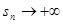и 
при . А это означает, что ряд 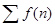расходится вместе с рядом , для которого первый ряд по условию является минорантой. Теорема доказана.[1], [2].
|
|
|
