Уточнение корней методом касательных (метод Ньютона)

Метод касательных, связанный с именем Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Предположим, что функция f (x), имеющая корень v на отрезке [a,b], дифференцируема на этом отрезке, и её производная f’ (x) не обращается на нем в нуль.

Возьмём произвольную точку x ₀ отрезка [a,b] и запишем в ней уравнение касательной к графику функции f (x):

y = f (x ₀)+ f’ (x ₀) (x - x ₀).

Полагая в этом уравнении y =0, находим абсциссу x ₁ точки пересечения касательной с осью O x:

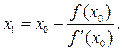
Повторим проделанную процедуру: напишем уравнение касательной к графику функции y = f (x) при x = x ₁ и найдём для неё точку пересечения x ₂ с осью О х:

Продолжая этот процесс, получим последовательность { x _n}, определенную с помощью рекуррентной формулы

(6)

Процесс вычисления продолжается до тех пор, пока не будет выполнено условие: | x _n+1 - x _n| < e. При выполнении этого неравенства итерационный процесс уточнения корня следует прекратить и в качестве искомого приближенного значения корня x ^* взять x ^*= x _n+1. Реализация алгоритма метода касательных представлена на блок-схеме в прил. 3.

Геометрически с помощью этого метода предлагаем построить касательную к кривой y=f(x) в выбранной точке x = x_n, найти точку пересечения её с осью абсцисс и принять эту точку за очередное приближение к корню (рис.9).

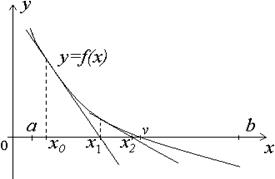
Рис. 9. Геометрическая иллюстрация метода касательных (метода Ньютона)

Очевидно, что этот метод обеспечивает сходящийся процесс приближений лишь при выполнении некоторых условий и при их нарушении либо дает расходящийся процесс (рис.10), либо приводит к другому корню (рис.11).

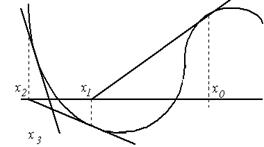
Рис. 10. Расходящийся процесс Рис. 11. Приближение к другому корню

Теорема (о сходимости метода касательных). Пусть функция f(x) дважды непрерывно дифференцируема на [a,b], причем её производные удовлетворяют неравенствам

| f ’(x)|³ m >0, | f ’’(x)|£ M, x Î[a,b].

Предположим, что корень x = v уравнения (1) является внутренней точкой отрезка [a,b], т.е. a< v <b. Тогда, найдется такое d: 0<d£min(v -a,b- v), что при любом выборе начального приближения на отрезке [ v -d, v +d]Ì[a,b] существует бесконечная итерационная последовательность (6) и эта последовательность сходится к корню v.

Обычно, на практике, за начальное приближение x ₀ принимается такое значение из отрезка [a,b], для которого выполняется следующее условие:

f (x 0) f ’’(x)>0.

(7)

Чаще всего выбирают х ₀=a или x ₀=b в зависимости от того, для какой из этих точек выполняется условие (7).

Метод Ньютона эффективен для решения тех уравнений, для которых значение модуля производной | f' (x)| близ корня достаточно велико, т.е. график функции y = f (x) в окрестностях данного корня имеет большую крутизну.

Метод Ньютона является наиболее быстрым среди численных методов вычисления корня функционального уравнения. На практике необходимая точность достигается буквально после выполнения нескольких (не более 10) итераций.

2.4. У точнение корней методом простой итерации

Если каким-либо способом получено приближенное значение x ₀ корня уравнения (1), то уточнение корня можно осуществить методом простых итераций. Для этого уравнение (1) представляют в виде

x =j(x).

(8)

Возьмём произвольное значение x ₀ из области определения функции j(x) и будем строить последовательность чисел { x_n }:

xn +1=j(xn), n =0,1,2,…

(9)

Процесс итераций продолжается до тех пор, пока | x_{n +1} – x_n | < e, и в качестве искомого приближенного значения корня x ^* следует взять x ^*= x_{n +1}.

Для формулировки условий сходимости итерационной последовательности (9) нам нужно вспомнить один результат из математического анализа (формула конечных приращений Лагранжа). Предположим, что функция j(x) дифференцируема на [a,b]. При сделанных предположениях о дифференцируемости справедлива следующая формула, называемая формулой конечных приращений Лагранжа (см. [5], теорема 15, с.29)

j(x ₂)- j(x ₁)=j’(x)(x ₂- x ₁), xÎ[ x ₁, x ₂]Ì[a,b].

Используя эту формулу, существование корня уравнения (8) можно установить с помощью предварительного исследования (8) с применением такого факта

Теорема (о сходимости метода простой итерации). Пусть x = v – корень уравнения (8) и пусть функция j(x) имеет в окрестности корня [ v -d, v +d], d>0, производную j’(x), удовлетворяющую условию

|j’(x)|£ q <1.

(10)

Тогда при любом выборе x ₀ на отрезке [ v -d, v +d] существует бесконечная итерационная последовательность { x_n } (9) и эта последовательность сходится к корню x = v, который является единственным решением уравнения (8) на отрезке [ v -d, v +d].

Сформулированная теорема имеет очень простой смысл. Будем говорить, что функция j осуществляет отображение точки x на точку y =j(x). Тогда условие (10) означает, что отображение j является сжимающим: расстояние между точками x ₁ и x ₂ больше, чем расстояние между их изображениями y ₁=j(x ₁) и y ₂=j(x ₂). Корень v является неподвижной точкой отображения j, он преобразуется сам в себя: v =j(v). Поэтому каждый шаг в итерационном процессе (9), сжимая расстояния, должен приближать члены последовательности { x_n } к неподвижной точке v.

Таким образом, итерационный процесс (9) сходится, если на отрезке [a,b], содержащем корень v и его последовательные приближения, выполнено условие (10). Важно отметить следующее. Если выполнено условие (10), но |j’(x)| близко к 1, то метод итераций применить можно, но итерационная последовательность (9) сходится медленно, для получения достаточной точности нужно вычислить большое число членов последовательности. Если же |j’(x)| мало, существенно меньше единицы, то итерационная последовательность сходится быстро, и в этом случае применение метода простых итераций выгодно. В качестве x ₀ можно взять произвольное значение из интервала, содержащего корень. Реализация алгоритма метода простой итерации представлена на блок-схеме в прил. 4. Отметим, что условие (10) является достаточным, но не необходимым. То есть, существуют функции, для которых условие (10) не выполнено, а итерационный процесс (9) сходится.

Отметим также, что для приведения нелинейного уравнения (1) к виду (8), чтобы выполнялось условие (10), существует много способов. Иногда используют следующий приём: заменяют f (x)=0 на x = x - kf (x). То есть j(x)= x - kf (x) и j’(x) =
=1-k f ’(x). Из решения неравенства (10), а именно | j’(x) | < 1, или |1-k f ’(x) | < 1, получают неравенство 0<k< 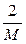, где . Для определения оптимального значения k используют условие |1-kM|=|1-km|, где , 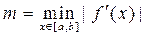. При этом k=2/(M+m).

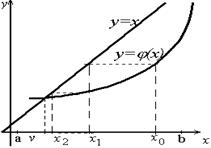
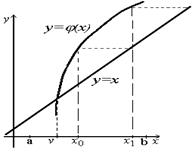
Геометрическая интерпретация процесса представлена на Рис. 12.

а) б) в)

Рис. 12. Геометрическая интерпретация метода простой итерации

Здесь на первых двух рисунках (а, б) показано одностороннее и двустороннее приближение к корню, на третьем (в) — расходящийся процесс (| j’(x) | > 1).

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: