Главная | Обратная связь | Поможем написать вашу работу!

Образец выполнения лабораторной работы №4

1. Постановка задачи для конкретного варианта.

Предварительно локализовав отрезок, содержащий первый положительный корень нелинейного уравнения e^- ^x - x =0, разработать проект VBA, позволяющий уточнить его с заданной точностью, используя: а) метод половинного деления;
б) метод хорд; в) метод касательных; г) метод простой итерации.

Выбор метода решения нелинейного уравнения осуществить с помощью элементов управления OptionButton, помещённых на пользовательскую форму (UserForm).Элементы управления OptionButton сгруппировать с помощью элемента управления Frame. Для каждого из перечисленных выше численных методов спроектировать отдельную пользовательскую форму (UserForm) на которой разместить необходимые объекты (элементы управления Label – для подписи на форме комментариев для пользователя; элементы управления TextBox – для ввода точности, и вывода найденного корня и числа итераций, за которое удалось найти требуемое значение корня с заданной точностью; элементы управления CommandButton – для выхода, вычисления корня и перехода на следующую и предыдущую формы). Необходимые вычисления оформить процедурами функциями.

2. Описание процесса отделения отрезка, содержащего первый положительный корень для конкретной функции из своего варианта.

Этот пункт проделать самостоятельно (см. лаб. раб. №1). Мы воспользуемся результатами предыдущих лабораторных работ (2 и 3). Имеем: f (x)= e^- ^x - x, начало отрезка a=0, конец отрезка b=1.

3. Обоснование сходимости (применимости метода) каждого из перечисленных в условии итерационных процессов в применении к конкретной функции и найденному отрезку. (Этот пункт также проделать самостоятельно (см. лаб. раб. №2).)

4. Эскизы всех пользовательских форм (UserForm) с подписанными именами нанесённых на них элементов управления.

а) UserForm1

Label1

Frame1

CommandButton2

CommandButton1

OptionButton1

OptionButton4

OptionButton2

OptionButton3

б) UserForm2

TextBox3

TextBox2

TextBox1

CommandButton3

CommandButton1

CommandButton2

Label3

Label2

Label1

в) UserForm3, UserForm4, UserForm5 спроектируйте аналогично UserForm2. (Все элементы управления и их имена аналогичны тем, что размещены на UserForm2. Поменять только свойство Caption соответствующих форм на название того метода который в данный момент реализуется.)

5. Тексты программ и блок-схемы всех необходимых процедур с указанием названия модуля в которых они сохранены.

Ниже приводятся тексты всех необходимых процедур. Блок-схемы тех процедур, в которых реализуются тот или иной численный метод решения нелинейных уравнений приводятся в прил 1-4. Естественно, что они требуют адаптации под написанные ниже тексты программ. Недостающие блок-схемы оформить самостоятельно.

а) Модуль UserForm1

Private Sub CommandButton1_Click()

UserForm1.Hide

End Sub

Private Sub CommandButton2_Click()

UserForm1.Hide

If OptionButton1.Value = True Then

UserForm2.Show

ElseIf OptionButton2.Value = True Then

UserForm3.Show

ElseIf OptionButton3.Value = True Then

UserForm4.Show

ElseIf OptionButton4.Value = True Then

UserForm5.Show

End If

End Sub

Private Sub UserForm_Initialize()

OptionButton1.Value = True

End Sub

б) Модуль UserForm2

Private Sub CommandButton1_Click()

UserForm2.Hide

UserForm1.Show

End Sub

Private Sub CommandButton3_Click()

UserForm2.Hide

UserForm3.Show

End Sub

Private Sub CommandButton2_Click()

Dim c As Single

Dim n As Integer

a = 0

b = 1

eps = Val(TextBox1.Text)

n = 0

Do While (b - a)>= eps

xn = (a + b) / 2

n = n + 1

If f(a)*f(xn)<= 0 Then b = xn Else a = xn

Loop

TextBox2.Text = xn

TextBox3.Text = n

End Sub

Private Sub UserForm_Initialize()

TextBox2.Enabled = False

TextBox3.Enabled = False

End Sub

в) Модуль UserForm3

Процедуры обработки событий для CommandButton1 и 3, а также пользовательской формы (Initialize) написать самостоятельно.

Private Sub CommandButton2_Click()

a = 0

xn=1

eps = Val(TextBox1.Text)

n = 0

xn = xn - f(xn) * (xn - a) / (f(xn) - f(a))

n = n + 1

Loop While Abs(f(xn)) >= eps

TextBox2.Value = xn

TextBox3.Value = n

End Sub

г) Модуль UserForm4

Процедуры обработки событий для CommandButton1 и 3, а также пользовательской формы (Initialize) написать самостоятельно.

Private Sub CommandButton2_Click()

xn=0

eps = Val(TextBox1.Text)

n = 0

Do Until Abs(f(xn)) < eps

xn = xn - f(xn) / производная_f(xn)

n = n + 1

Loop

TextBox2.Value = xn

TextBox3.Value = n

End Sub

д) Модуль UserForm5

Процедуры обработки событий для CommandButton1 и 3, а также пользовательской формы (Initialize) написать самостоятельно.

Private Sub CommandButton2_Click()

a=0

b=1

eps = Val(TextBox1.Text)

xn = (a + b) / 2

n = 0

xn = fi(xn)

n = n + 1

Loop Until Abs(f(xn))< eps

TextBox2.Value = xn

TextBox3.Value = n

End Sub

е) Module1

Public Function f(ByVal x As Single) As Single

f = Exp(-x) - x

End Function

Public Function производная_f(ByVal x As Single) As Single

производная_f = -Exp(-x) - 1

End Function

Public Function fi(ByVal x As Single) As Single

fi = Exp(-x)

End Function

6. Результаты работы для каждого из методов решения нелинейных уравнений выписать в следующем виде:

Решение уравнения e^- ^x - x =0	Название численного метода
метод половинного деления	метод хорд	метод касательных	метод простой итерации
Вычисленное значение корня	0,5672	0,5672	0,5671	0,5671
Число итераций

7. Расписать структуру полученного проекта.

8. Отразить на схеме взаимосвязь имеющихся модулей.

9. Проанализировать полученные результаты и сравнить с результатами предыдущих лабораторных работ.

Таблица 3

ВАРИАНТЫ ЗАДАНИЙ для лабораторных работ №2, №3, №4

№ вар.	Уравнение	a	b	№ вар.	Уравнение	A	b
	cos x = x - 4;				arctg(x ²+ )= x;
	0,5 – x = ln(x +1);				x 2 ^x – 1 = 0;
	sin(x + 1) = 0,5 x;				ln(x + 2) = (1 - x)³;
	2arctg x = x - 3;				x^x + 9 x = 20;
					(x - 3)cos x - ½ = 0;
	tg(0,58 x +0,1)= x ²;				lg(x + 1) = 10^{- x};
	3 ^x + 2 x = 2;				tg³(x + 4,5) = x - 1;
	1 + x ⁵= 3 x;				5 ^x = e ^{- x}+ 1;
	ln x = sin x;				x – 1 = x ^0,15;
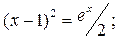
					ln x = .

Таблица 4

Ответы к лабораторной работе №1

№ вар.	Ответ	№ вар.	Ответ
	[-4,3]; [2,3];		[0.1,1]; [4,5];
	[3,4];		[-2,-1];
	корней нет;		[1,2];
	[-1,0]; [1,2];		[2,3];
	[-3,-2]; [-1,0]; [2,3];		[0,1];
	[1;2];		[0,1];
	[-2,-1]; [1,2]		корней нет;
	[-1,0]; [3,4];		[-3,-2]; [1,2];
	[1,2];		[-1,-0.1]; [0.1,1];
	[1,2];		[2,3].

Таблица 5

Ответы к лабораторным работам №2, №3, №4^*

№ вар.	Ответ	№ вар.	Ответ	№ вар.	Ответ	№ вар.	Ответ
	3.0088;		0.7904;		1.1402;		0.6582;
	0.2650;		0.3027;		0.6412;		2.6518;
	1.3800;		1.2146;		0.0956;		0.3352;
	5.8001;		2.2191;		1.8662;		2.1192;
	4.6815;		0.2133;		4.9691;		1.7632.

^*Корень уравнения, приведенный в качестве ответа, найден при помощи метода половинного деления с заданной точностью

Использованная литература

1. Костомаров Д.П., Корухова Л.С., Манжелей С.Г. Программирование и численные методы. – М.: МГУ, 2001. – 224 с.

2. Беляев Б.А., Власков Г.А., Медведева Т.А., Цвиль М.М. Численные методы с программированием на Паскале. – Ростов н/Д: РГСУ, 1995.

3. Воробьёва Г.Н., Данилова А.Н. Практикум по вычислительной математике: учеб. пособие для техникумов. 2-е изд., перераб. и доп. – М.: Высш. школа, 1990. – 208 с.

4. Гарнаев А.Ю. Excel, VBA, Internet в экономике и финансах. - СПб.: БХВ-Петербург, 2001.

5. Белявский Г.И., Павлов И.В. Теория пределов и дифференциальное исчисление (курс лекций и контрольное задание №2 по высшей математике для студентов всех форм обучения). – Ростов н/Д: РГСУ, 2003.

6. Шамраева В.В., Зиньковская Н.П. Объектно-ориентированное программирование для Microsoft Excel. – Ростов н/Д: РГСУ, 2006. – 100 с.

Приложение 1

⇐ Предыдущая 1 2 3 4 5 6 7 89

Воспользуйтесь поиском по сайту: