 |
Некоторые характеристики турбулентного потока
|
|
|
|
Режимы движения жидкости.
Впервые изучено Рейнольдсом (1883 г.) подкрашиванием жидкости, вытекающей при постоянном уровне.
Различают: Ламинарное движение => все частицы жидкости движутся по параллельным траекториям и турбулентное движение => отдельные частицы жидкости движутся по хаотическим траекториям, в то время как вся масса жидкости в целом перемещается в одном направлении.
Особенностью турбулентного потока является наличие поперечных перемещений частиц жидкости, приводящих к интенсивному перемешиванию потока по сечению. Для этого требуется большая затрата энергии.
Режим движения жидкости количественно характеризуется значением критерия 
(безразмерный комплекс).
Критерий Re является мерой соотношения между силами вязкости и инерции в движущемся потоке.
Вероятность турбулизации возрастает с уменьшением вязкости жидкости и с увеличением плотности (мера инерционного отклонения от прямолинейной траектории частиц).
Переход от ламинарного течения происходит скачкообразно, характеризуется критическим значением Re.
По прямым гладким трубам 
.
При Re<2320 => устойчивый ламинарный режим.
2320<Re<10000 => режим течения неустойчивого турбулентного или переходного (смешанный): при этом может наблюдаться с меньшей вероятностью ламинарное течение.
Re>10000 => устойчивая (развитая) турбулентность.
При движении жидкости через каналы некруглого сечения при расчёте Re используют эквивалентный диаметр:
=4 
;
Гидравлический радиус – отношение площади свободного сечения трубопровода или канала, через которое протекает жидкость, к смоченному периметру:
Для круглой трубы: 
;
Квадрата: 
Канала прямоугольного сечения: 
= 
;
|
|
|
Кольцевого сечения: 
В критерий Re входит (как и в уравнение расхода) средняя ёмкость, а действительные скорости различны по сечению, причём их распределение различно для ламинарного и турбулентного течений.
Для ламинарного потока вид распределения скоростей может быть установлен теоретически.
Распределение скоростей и расход жидкости при установившемся ламинарном потоке
Выделим в потоке жидкости, ламинарно движущемся по трубе радиусом R, цилиндрический слой длиной L и радиусом r,причём скорость движения жидкости на расстоянии r равна 
Движение слоя жидкости происходит под действием разности сил давления с обеих сторон цилиндра:
где 
гидростатические давления.
Одновременно движению цилиндра оказывает сопротивление сила внутреннего трения, действующая по поверхности:
Т=- 
; где: F=2 
- наружная поверхность цилиндра (знак «-» указывает на убывание скорости с увеличением радиуса: по направлению к стенке).
При установившемся потоке имеем: 
(
) 
; разделяя переменные и интегрируя:
Или: 
; (1)
Отсюда следует, что скорость имеет максимальное значение на оси трубы, где r=0;
Отсюда: 
= 
(2)
Сопоставляя (1) и (2), находим:
Это закон Стокса, выражающий параболическое распределение скоростей в сечении трубопровода при ламинарном движении.
Эпюра скоростей имеет вид:
Определим расход жидкости через трубу:
Выделим кольцевое сечение толщиной dr и окружностью 2 
.
Расход через кольцевое сечение:
d 
= 
интегрируем: 
Уравнение Пуазейля.
С другой стороны:
Отсюда средняя скорость:
!!!!!!
При ламинарном течении средняя скорость равна половине максимальной (по оси трубы)!!!!!
Некоторые характеристики турбулентного потока
Турбулентное движение наиболее широко распространено в технике.
Из-за хаотического движения частиц происходит выравнивание скоростей в основной массе потока. Опыты показывают, что средняя скорость больше, чем 
и зависит от Re:
|
|
|
Например, при Re = 
Re = 
Теоретически профиль (эпюру) скоростей получить не удаётся из-за чрезвычайной сложности.
В основной массе потока скорости жидкости в значительной мере выравнены по сечению трубы. Однако вблизи стенки скорость резко снижается, обращаясь у самой стенки в нуль. В непосредственной близости от стенки движение жидкости становится всё менее турбулентным и всё более ламинарным, т.к. твёрдая стенка «гасит» турбулентные пульсации в поперечном направлении.
! Таким образом, турбулентное движение всегда сопровождается ламинарным.
Условно различают центральную зону «ядро» потока (основная масса жидкости) с развитым турбулентным движением и «пограничный слой» вблизи стенки, где происходит переход турбулентного движения в ламинарное.
Пограничный слой состоит из переходной зоны и ламинарного подслоя, который характеризуется очень малой толщиной (доли миллиметра), которая уменьшается с возрастанием турбулентного потока и очень большим градиентом скорости (до нуля у стенки). Большое значение этот подслой имеет при гидравлическом сопротивлении, а также тепло- и массобмене.
Уравнение Бернулли - интеграл уравнения движения Эйлера
Одно из наиболее важных и широко используемых в гидродинамике. Запишем дифференциальные уравнения движения Эйлера:
Для установившегося движения при условии, что компоненты скорости меняются только в направлении соответствующих осей, имеем:
Эти уравнения умножим на длину соответствующих граней, чтобы они выражали действие сил не в точке, а на всей длине граней:
Полное изменение действия сил во всём объёме элементарного параллелепипеда получим, сложив уравнения (и разделив на 
):
-gdz – 
1 2
Выражение в 1-ой скобке Полный дифференциал давления (
).
Выражение 
В соответствии с этим выражение во 2-ой скобке полный дифференциал квадрата скорости.
Следовательно:
gdz+ 
или: dz+d(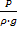
)+d(
)=0;
или: d(z+ 
+ )=0;
Z+ 
Это уравнение Бернулли для установившегося потока идеальной жидкости (без вязкости).
Для любых 2-х поперечных сечений потока:
(Z+ 
) полный гидродинамический напор (или просто гидродинамический напор).
|
|
|
Для всех поперечных сечений установившегося потока идеальной жидкости величина полного гидродинамического напора остаётся неизменной.
Полный гидродинамический напор включает в себя 3 слагаемых:
Z нивелирная высота (геометрический напор) или удельная потенциальная энергия положения в данной точке (сечений).
статический (пьезометрический напор) или удельная потенциальная энергия давлений в данной точке (сечений);
скоростной (динамический) напор или удельная кинетическая энергия в данной точке (сечения).
При установившемся движении идеальной жидкости сумма нивелирной высоты, скоростного и статического напоров, равная гидродинамическому напору, не меняется при переходе от одного поперечного сечения потока к другому.
При установившемся движении сумма потенциальной и кинетической энергий жидкости для каждого из поперечных сечений потока остаётся неизменной.
Таким образом, уравнение Бернулли является частным случаем закона сохранения энергии и выражает энергетический баланс потока.
При изменении поперечного сечения и, соответственно, изменении скорости движения происходит превращение энергии: при сужении трубопровода часть потенциальной энергии переходит в кинетическую и наоборот!!!!
! Для горизонтального трубопровода уравнение Бернулли упрощается:
+ 
|
|
|
