Естественный способ задания движения точки

КИНЕМАТИКА

Кинематика – раздел механики, в котором изучаются движение материальных тел с геометрической точки зрения, без учета массы и действующих на них сил.

Плоское движение твердого тела.

Плоским (плоскопараллельным) назыв. такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости. Уравнения плоского движения: x_A= f₁(t), y_A= f₂(t), j = f₃(t), точка А назыв. полюсом. Плоское движение тв.тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс (А),и из вращательного движения вокруг этого полюса.

Плоским или плоскопараллель­ным движением твердого тела называ­ется такое его движение, при котором ка­ждая точка тела движется в плоско­сти, параллельной некоторой неподвижной плоскости, например движение колеса ва­гона на прямолинейном участке пути, дви­жение шатуна кривошипно-шатунного ме­ханизма.

Способы задания движения точки: 1) естественный, 2) координатный, 3) векторный. Траектория точки – непрерывная кривая, которую описывает точка при своем движении.

Естественный сп. указывается траектория точки, закон ее движения по этой траектории, начало и направление отсчета дуговой координаты: s=f(t) – закон движения точки. При прямолинейном движении: х=f(t).

Координатный сп. положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=f₁(t), y=f₂(t), z=f₃(t).

Если движение в плоскости, то два уравнения движения. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр t, получаем уравнение траектории в обычном виде: f(x,y)=0 (для плоск-ти).

Векторный сп. положение точки определяется ее радиус-вектором 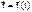, проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, назыв. годографом этого вектора. Т.е. траектория – годограф радиус-вектора. Связь между координатным и векторным способами: ,

( – орты – единичные вектора, сонаправленные с какой-либо осью)

модуль , направляющие косинусы: 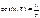и т.д.

Переход от координатного способа к естественному: .

Сложение поступательных движ

От сложения 2х поступательных движений твердого тела получается поступательное движение со скоростью, равной векторной сумме скоростей состовляющих поступательных движений.

Естественный способ задания дв-я точки.

При естеств.способе задания дв-я точки д.б.задано: 1)траектория дв-я точки, 2)начало отсчета на траектории, 3)положительное и отрицательное направление отсчета, 4)дуговая абсцисса д.б.задана как ф-ция от времени S=f(t)

Введем единичный орт касательный t. Вектор t направлен в сторону возрастания дуговой абсциссы, модуль êtê=1

Вектор скорости V опр-ся: V=s t.

Если s>0, то скорость направлена в сторону возрастания дуговой абсциссы по вектору t, а если s<0, то вектор скорости напрвлен в сторону убывания дуговой абсциссы.

V=s- алгебраическое зн-е скорости.

Естественный способ задания движения точки

Рассмотрим, как вычисляются скорость и ускорение точки при естественном способе задания ее движения, то есть когда заданы траектория точки и закон движения точки вдоль этой траектории в виде s = s(t).

В этом случае векторы v и a определяют по их проекциям не на оси системы координат Oxyz, а на подвижные оси P nb, имеющие начало в точке Р и движущиеся вместе с нею (см.рис.). Эти оси, называемые осями естественного трехгранника, направлены следующим образом:

· ось P направлена по касательной к траектории в сторону положительного направления отсчета координаты s;

· ось Pn направлена по нормали к траектории, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории;

· ось Pb направлена перпендикулярно к первым двум осям P и Pn так, чтобы она образовала правую систему осей (с положительного направления оси Pb поворот оси P к оси Pn в их плоскости на прямой угол виден происходящим против хода часовой стрелки).

Нормаль Pn, лежащая в соприкасающейся плоскости (в плоскости самой кривой, если кривая плоская),называется главной нормалью, а перпендикулярная ей нормаль Pb - бинормалью.

Определение скорости точки при естеств

Вектор скорости v точки направлен по касательной к траектории и определяется одной проекцией , равной первой производной от криволинейной координаты s этой точки по времени:

= ds / dt = .

Величину , которая может быть как положительной, так и отрицательной, называют числовым (или алгебраическим) значением скорости.

Модуль скорости v = | | и, следовательно, значения v и могут отличаться лишь знаком:

v = , если точка движется в положительном направлении отсчета координаты s, или
v = - , если точка движется в противоположном направлении.

Таким образом, величина определяет одновременно и модуль скорости, и сторону, в которую направлен вектор v вдоль касательной.

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: