 |
Описание математических методов решения задачи
|
|
|
|
Помощи неявной схемы Адамса 3-го порядка»
МОСКВА 2008
Содержание
Введение
1. Постановка задачи
2. Описание математических методов решения
3. Описание используемого метода
4. Описание блок-схемы
5. Описание программы
6. Анализ результатов
Заключение
Литература
Приложения
Приложение 1
Приложение 2
Приложение 3
Введение
Бурное развитие в последнее десятилетие информационных технологий и компьютерной техники способствует возникновению всё более сложных математических задач, для решения которых без применения численных методов требуется значительное время. Очень часто перед специалистом возникают задачи, не требующие абсолютно точного решения; как правило, требуется найти приближенное решение с заданной погрешностью. Наряду с совершенствованием компьютерной техники происходит процесс совершенствования и численных методов программирования, позволяющих за минимальный отрезок времени получить решение поставленной задачи с заданной степенью точности.
Одной из таких задач является решение систем дифференциальных уравнений. Обыкновенными дифференциальными уравнениями можно описать поведение материальных точек в силовом поле, законы химической кинетики, уравнения электрических цепей и т. д. Ряд физических задач может быть сведён к решению дифференциальных уравнений или системы дифференциальных уравнений. Задача решения системы дифференциальных уравнений имеет важное прикладное значение при решении научных и технических проблем. Кроме того, она является вспомогательной задачей при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований. Поэтому для инженеров крайне важно грамотно находить решение этой задачи.
|
|
|
Постановка задачи
Необходимо решить с заданной степенью точности задачу Коши для системы дифференциальных уравнений на заданном интервале [a,b]. Добиться погрешности на втором конце не более 0,0001. Результат получить в виде таблицы значений приближенного и точного решений в точках заданного интервала. Построить графики полученных решений и сравнить их с точным решением.
Исходные данные:
– система дифференциальных уравнений вида:

– интервал, на котором ищется решение: [a,b]
– погрешность, с которой ищется решение: е
– формулировка задачи Коши в начальной точке заданного интервала:  u(a)=u, v(a)=v
u(a)=u, v(a)=v
– количество узлов сетки, для которой формируется таблица значений приближенного и точного решений системы: nx
– шаг вывода на экран значений искомых функций в узлах заданной сетки: np
Выходные данные:
– таблица значений приближенного и точного решений в узлах заданной сетки;
– графики полученных и точных решений.
Описание математических методов решения задачи
Конкретная прикладная задача может привести к дифференциальному уравнению любого порядка или к системе таких уравнений. Произвольную систему дифференциальных уравнений любого порядка можно привести к некоторой эквивалентной системе дифференциальных уравнений первого порядка. Среди таких систем выделяют класс систем, разрешённых относительно производной неизвестных функций:
 (2.1)
(2.1)
Дифференциальное уравнение или система дифференциальных уравнений имеет бесконечное множество решений. Единственные решения выделяют с помощью дополнительных условий, которым должны удовлетворять искомые решения. В зависимости от вида таких условий рассматривают три типа задач, для которых доказано существование и единственность решений.
|
|
|
Первый тип – это задачи Коши, или задачи с начальными условиями. Для таких задач кроме исходного уравнения в некоторой точке a должны быть заданы начальные условия, т.е. значения функции u1(a),…, um(a):
u1(a)=  ,…, um(a)=
,…, um(a)=  (2.2)
(2.2)
Ко второму типу задач относятся так называемые граничные, или краевые задачи, в которых дополнительные условия задаются в виде функциональных соотношений между искомыми решениями. Количество условий должно совпадать с порядком n уравнения или системы. Если решение задачи определяется в интервале xÎ[a,b], то такие условия могут быть заданы как на границах, так и внутри интервала.
Третий тип задач для систем дифференциальных уравнений – это задачи на собственные значения. Такие задачи отличаются тем, что кроме искомых функций u1(x),…, um(x) в уравнения входят дополнительно n неизвестных параметров l1, l2,..., ln, которые называются собственными значениями. Для единственности решения на интервале [a,b] необходимо задать n + m граничных условий.
Рассмотрим подробнее задачу Коши. Воспользуемся компактной записью задачи (2.1), (2.2) в векторной форме:
 (2.3)
(2.3)
Требуется найти  на интервале [a,b].
на интервале [a,b].
Задачу Коши удобнее всего решать методом сеток. Метод сеток состоит в следующем:
1) Выбираем в области интегрирования упорядоченную систему точек a=x1<x2<…<xn<b, называемую сеткой. Точки xi называют узлами разностной сетки, разность между соседними узлами h=xi-xi-1 – шаг сетки. Формула для вычисления шага равномерной сетки, заданной на интервале [a,b]:
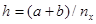 , (2.4)
, (2.4)
где nx – количество узлов заданной сетки.
2) Решение  ищется в виде таблицы значений в узлах выбранной сетки, для чего дифференцирование заменяется системой алгебраических уравнений, связывающих между собой значения искомой функции в соседних узлах. Такую систему уравнений принято называть конечно-разностной схемой.
ищется в виде таблицы значений в узлах выбранной сетки, для чего дифференцирование заменяется системой алгебраических уравнений, связывающих между собой значения искомой функции в соседних узлах. Такую систему уравнений принято называть конечно-разностной схемой.
Для получения конечно-разностной схемы удобно использовать интегроинтерполяционный метод, согласно которому необходимо проинтегрировать уравнение (2.3) на каждом интервале [xk, xk+1] и разделить полученное выражение на длину этого интервала:
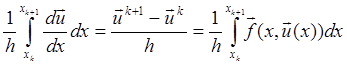 (2.5)
(2.5)
Далее апроксимируем интеграл в правой части одной из квадратурных формул и получаем систему уравнений относительно приближенных неизвестных значений искомых функций, которые в отличие от точных обозначим  . При этом возникает погрешность ε, обусловленная неточностью апроксимации:
. При этом возникает погрешность ε, обусловленная неточностью апроксимации:
|
|
|
ε(h)=||  || (2.6)
|| (2.6)
Согласно основной теореме теории метода сеток (теорема Лакса), для устойчивой конечно-разностной схемы при стремлении шага h к нулю погрешность решения стремится к нулю с тем же порядком, что и погрешность апроксимации:
 , (2.7)
, (2.7)
где С0 – константа устойчивости, p – порядок апроксимации.
Поэтому для увеличения точности решения необходимо уменьшить шаг сетки h.
На практике применяется множество видов конечно-разностных схем, которые подразделяются на одношаговые, многошаговые схемы и схемы с дробным шагом.
Одношаговые схемы
– Метод Эйлера
Заменяем интеграл в правой части уравнения (2.5) по формуле левых прямоугольников:
 (2.8)
(2.8)
Получим:
 , (2.9)
, (2.9)
где k=0,1,2,…,n.
Схема явная устойчивая. В силу того, что формула для левых прямоугольников имеет погрешность второго порядка, точность ε(h) первого порядка. 
– Неявная схема 1-го порядка
Используя формулу правых прямоугольников, получим:
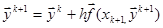 (2.10)
(2.10)
Эта схема неразрешима в явном виде относительно  , поэтому проводится итерационная процедура:
, поэтому проводится итерационная процедура:
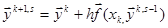 , (2.11)
, (2.11)
где s=1,2,… - номер итерации. Обычно схема сходится очень быстро – 2-3 итерации. Неявная схема первого порядка эффективнее явной, так как константа устойчивости С0 у неё значительно меньше.
– Метод Эйлера-Коши
Вычисления проводятся в два этапа: этап прогноза и этап коррекции.
На этапе прогноза определяется приближенное решение на правом конце интервала по методу Эйлера:
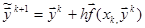 (2.12)
(2.12)
На этапе коррекции, используя формулу трапеций, уточняем значение решения на правом конце:
 (2.13)
(2.13)
Так как формула трапеций имеет третий порядок точности, то порядок погрешности апроксимации – равен двум.
– Неявная схема 2-го порядка (метод Эйлера-Коши)
Используя в (2.5) формулу трапеций, получим:
|
|
|
 (2.14)
(2.14)
Схема не разрешена в явном виде, поэтому требуется итерационная процедура:
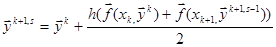 , (2.15)
, (2.15)
где s=1,2,… – номер итерации. Обычно схема сходится за 3-4 итерации.
Так как формула трапеций имеет третий порядок точности, то погрешность апроксимации – второй.
Схемы с дробным шагом
– Схема предиктор-корректор (Рунге-Кутта) 2-го порядка
Используя в (2.5) формулу средних, получим:
 ,(2.16)
,(2.16)
где  – решение системы на середине интервала [xk, xk+1]. Уравнение явно разрешено относительно
– решение системы на середине интервала [xk, xk+1]. Уравнение явно разрешено относительно  , однако в правой части присутствует неизвестное значение
, однако в правой части присутствует неизвестное значение  . Поэтому сначала расчитывают
. Поэтому сначала расчитывают  (предиктор):
(предиктор):
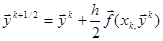 . (2.17)
. (2.17)
Затем расчитывают  (корректор) по формуле (2.16). Схема имеет первый порядок погрешности.
(корректор) по формуле (2.16). Схема имеет первый порядок погрешности.
– Схема Рунге-Кутта 4-го порядка
Используя в (2.5) формулу Симпсона, получим:
 (2.18)
(2.18)
Наиболее часто рассчитывают неявное по  уравнение по следующей схеме:
уравнение по следующей схеме:
Сначала рассчитывают предиктор вида:
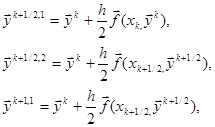 (2.19)
(2.19)
затем корректор по формуле:
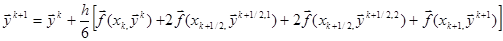 (2.20)
(2.20)
Поскольку формула Симпсона имеет пятый порядок погрешности, то точность ε(h) – четвёртого порядка.
Многошаговые схемы
Многошаговые методы решения задачи Коши характеризуются тем, что решение в текущем узле зависит от данных не в одном предыдущем или последующем узле сетки, как это имеет место в одношаговых методах, а зависит от данных в нескольких соседних узлах.
Идея методов Адамса заключается в том, чтобы для повышения точности использовать вычисленные уже на предыдущих шагах значения 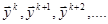
Если заменим в (2.5) подинтегральное выражение интерполяционным многочленом Ньютона, построенного по узлам  , то после интегрирования на интервале
, то после интегрирования на интервале 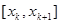 получим явную экстраполяционную схему Адамса. Если заменим в (2.5) подинтегральное выражение на многочлен Ньютона, построенного по узлам
получим явную экстраполяционную схему Адамса. Если заменим в (2.5) подинтегральное выражение на многочлен Ньютона, построенного по узлам  , то получим неявную интерполяционную схему Адамса.
, то получим неявную интерполяционную схему Адамса.
– Явная экстраполяционная схема Адамса 2-го порядка

 (2.21)
(2.21)
Схема двухшаговая, поэтому необходимо для расчётов найти по схеме Рунге-Кутта 2-го порядка  , после чего
, после чего  ,
,  , … вычисляют по формуле (2.21)
, … вычисляют по формуле (2.21)
– Явная экстраполяционная схема Адамса 3-го порядка
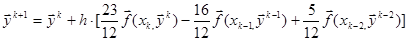 (2.22)
(2.22)
Схема двухшаговая, поэтому необходимо сперва найти  и
и 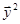 по схеме предиктор-корректор 4-го порядка, после чего
по схеме предиктор-корректор 4-го порядка, после чего  ,
,  , … вычисляют по формуле (2.22).
, … вычисляют по формуле (2.22).
|
|
|


