 |
Расчет координат промежуточных точек ортодромии
|
|
|
|

Для прокладке на меркаторской карте дуги большого круга по промежуточным точкам существует ряд методов. Рассмотрим один из них, основанный на использовании таблиц помещенных в МТ-75.
Предположим что необходимо нанести на карту ортодромию, соединяющую точки А и В (рис.2.7.1). найдем вначале уравнение дуги большого круга, связывающее текущие координаты точки М(φ;λ) с параметрами λо и Ко.
Из прямоугольного сферического треугольника OFM имеем:
tg φ = sin(λ - λ0) ctg K0, (2.7.1)
где φ и λ – текущие координаты произвольной точки дуги большого круга, соединяющей пункты А и В; λ0 – долгота точки пересечения дуги большого круга с экватором; K0 – угол между меридианом и дугой большого круга в этой точке.
Задаваясь долготой по формуле 2.7.1 можно найти широту промежуточной точки или, задаваясь ее широтой рассчитать долготу.
Из формулы 2.7.1: sin(λ - λ0) = tg φ tg K0 (2.7.2)
По формулам 2.7.1 и 2.7.2 составлены таблицы в МТ, которые значительно упрощают расчеты. Чтобы воспользоваться таблицами, нужно предварительно найти параметры K0 и λ0. Из прямоугольных сферических треугольников OAR и OBT имеем:
tg φ1 = ctg K0 sin(λ1 - λ0) (2.7.3)
tg φ2 = ctg K0 sin(λ2 - λ0)
где φ1 и λ1 – известные координаты точки А; φ2 и λ2 – координаты точки В.
Для определения λ0 найдем из формулы 2.7.3 отношение разности широт к их сумме:
tg φ2 - tg φ1 sin(λ2 - λ0) - (λ1 - λ0) 2 cos((λ1 + λ2) / 2 - λ0) cos((λ2 - λ0) /2)
—————— = —————————— = ——————————— =
|
|
|
tg φ1 + tg φ2 sin(λ2 - λ0) + (λ1 - λ0) 2 sin(((λ1 + λ2) / 2 - λ0) sin ((λ2 - λ0) /2)
= ctg(((λ1 + λ2) / 2 - λ0) sin ((λ2 - λ0) /2).
Кроме того, для этого отношения можно получить и другое выражение:
tg φ2 - tg φ1 sin(φ2 - φ1)
————— = —————
tg φ1 + tg φ2 sin(φ2 + φ1)
приравнивая оба выражения получим формулу для расчета λ0
 (2.7.4)
(2.7.4)
После определения по формуле 2.7.4 из любого соотношения 2.7.3 можно найти K0.
При расчете сумм и разностей широт и долгот, входящих в формулу 2.7.3, следует обратить внимание на наименования географических координат, учитывая их знаки. Можно все долготы считать по часовой стрелке, как остовые от 0 до 360°. Так как дуга большого круга пересекает экватор в двух точках, то формула 2.7.4 даст два значения λ0, отличающихся друг от друга на 180°.
Из практических соображений достаточно вычислить промежуточные точки через 10° долготы (широты). Курс в любой точке ортодромии можно получить по формуле, которую можно получить из прямоугольного сферического треугольникаOFM:
tg K = tg (λ - λ0) cosec φ (2.7.5)
Па практике, когда дуга большого круга по промежуточным точкам нанесена на карту и заменена отрезками локсодромии (хорд), курс на каждом отрезке снимают транспортиром.
Чтобы определить количество промежуточных точек, которые нужно наносить, и допустимую длину отрезков локсодромий, следует поступить следующим образом. По формулы приближенной для ортодромической поправки:
S - D
Δ% = ——— *100 = 0.0048 Ψ° (2.7.6)
D
По формуле 2.7.6 составлена таб.1, из которой по найденному значению ортодромической поправки можно найти приближенное значение Δ%.
Таб. 2.7.1
| Ψ° | % | Ψ° | % |
| 5° | 0,1 | 30° | 4,3 |
| 10° | 0,5 | 40° | 7,7 |
| 20° | 1,9 | 50° | 7,7 |
|
|
|
Как видно из таб.2.7.1, плавание по дуге большого круга дает заметное сокращение расстояния (0,5 и больше), только начиная со значения Ψ=10°.
Из приближенной формулы для ортодромической поправки, полагая Ψ=5°, найдем допустимую разность долгот между промежуточными точками
РД = 10° / sinφ. (2.7.7)
Следовательно, обычно принимаемый интервал РД(РШ) = 10° для вычисления промежуточных точек вполне достаточен. Изменение курсов в промежуточных точках при плавании по отрезкам локсодромий будет определено принятой разностью долгот.
K1 – K2 ≈ 2Ψ ≈ РД sin φср
Вычисляем:
По формуле 2.7.4 находим λ0,точки в которых дуга большого круга пересекает экватор.
tg(67.1° - λ0) = tg(-48.7°) sin(-65.9°) cosec(-1.9°)
λ0 = 155°17.8'
Следовательно, дуга большого круга пересекает экватор в двух точках:
λ0 = 155°17.8' и λ0 = 335°17.8'.
По формуле 2.7.3 находим K0, угол между меридианом и дугой большого круга в точке λ0:
tg K0 = sin(115,8° - 155,3°) сtg 32,1°
K0 = 45°27,7
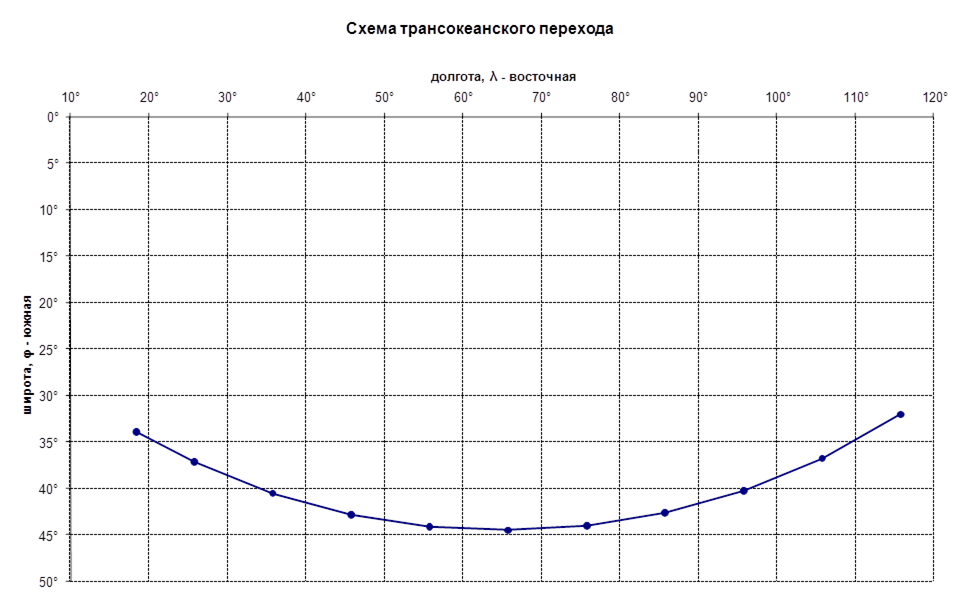
Так как дуга большого круга в данной задаче по направлению близка к параллели, целесообразно задаться долготой промежуточных точек и находить их широту по формуле 2.7.1 и результаты сводим в таблицу 2.7.2
|
| λi | φi | ||
| Порт Фримантл | 115° | 47' | -32° | -3 |
|
| 105° | 47' | -36° | -48,7 |
|
| 95° | 47' | -40° | -17,8 |
|
| 85° | 47' | -42° | -40,2 |
|
| 75° | 47' | -44° | -3,4 |
|
| 65° | 47' | -44° | -32,2 |
|
| 55° | 47' | -44° | -8,5 |
|
| 45° | 47' | -42° | -50,8 |
|
| 35° | 47' | -40° | -34,5 |
|
| 25° | 47' | -37° | -12,2 |
| Порт Кейптаун | 18° | 26' | -33° | -56 |
|
|
|


