 |
Принципы получения объективной оценки знаний студента
|
|
|
|
Оценка знаний студента, полученных им по той или иной учебной дисциплине, не только подводит итог его успеваемости, но зачастую определяет и его способность к дальнейшему обучению или самостоятельной деятельности, т.е. значительным образом влияет на судьбу человека. Поэтому нет сомнений в том, что такая оценка должна быть максимально объективной, залогом чего обычно служит опыт и интуиция экзаменатора. На деле же не только между различными дисциплинами, но и в пределах одной — между разными преподавателями — не существует унифицированного подхода к требованиям на экзамене, так как до сих пор не найдены или не выбраны количественные параметры даже для проведения научно обоснованной грани между неудовлетворительной и удовлетворительной оценками. Если в принятой нами четырехбальной системе «двойка» составляет от «пятерки» 40%, то это, разумеется, вовсе не означает, что студент для получения удовлетворительной оценки должен знать 40 и более процентов от объема изучаемого предмета. А сколько?
Воспользуемся терминами и понятиями, применяемыми в государственных образовательных стандартах: «знание» и «умение». Очевидно, преподавание учебной дисциплины заключается в передаче преподавателем учащимся определенной суммы знаний и, что более сложно, в обучении их умению использовать эти знания. Графически (рис. 1) это можно представить в виде линии АВ, показывающей повышение уровня знаний обучаемого в течение определенного времени (т) до предела СВ, определяемого учебной программой дисциплины, и линии OD — рост уровня умения обучаемого оперировать полученными знаниями[5].
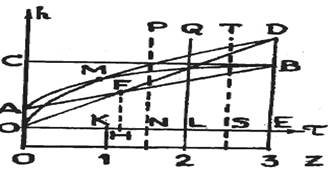
Рис. 1.
Изучение новой дисциплины начинается не на пустом месте, т.к. учащиеся в результате обучения предшествующим дисциплинам всегда имеют какой-то запас знаний (отрезок ОА = а), полезных для данной дисциплины. Объем начальных знаний студентов по изучаемой дисциплине (а) показывает входной контроль. Для входного контроля знаний по преподаваемой дисциплине должны быть составлены вопросы по ключевым темам ранее изучавшихся студентом родственных дисциплин и определена их доля от всей учебной программы данной дисциплины. Так, доля вопросов входного контроля для студентов 1-го курса ХТФ МГТУ им. А.Н. Косыгина от программы «Основ теоретической химии» составляет 25%, при тестировании было получено 47,9% правильных ответов, следовательно, начальный объем знаний по этой дисциплине составляет 12%.
|
|
|
Углы подъема кривых зависят от характера учебной дисциплины: чем больше она содержит элементов теории, чем менее в ней «описательности», тем больше величина DE превышает величину BE.
Очевидно, что при количественном выражении уровня умения и уровня знания первый должен превышать второй в том случае, если учащийся способен использовать свои знания для решения поставленных перед ним задач. Если по чисто описательной дисциплине для этого достаточно равенства уравнений, то для теоретических и расчетных дисциплин разница между ними может достигать 50%. В нашем случае для «Основ теоретической химии» DB составляет от BE 40%.
На наш взгляд, важнейшее значение имеет точка М, после «прохождения» которой уровень умения обучаемых становится выше уровня их знания. А это означает, что обучаемый приобрел умение использовать свои знания, иначе говоря, он перешел из области пассивных в область активных знаний.
Количественно приобретенный учащимся запас знаний и умений можно найти как сумму площадей ОАВЕ и ODE. В первом приближении расчет можно провести с аппроксимацией зависимостей АВ и OD через прямые линии с заменой точки М, показывающей переход пассивных знаний в активные, на точку F. В этом случае запас пассивных знаний и умений, ограниченный отрезком FH, от максимально возможного запаса знаний и умений составляет 21%, а отрезок ОН равен 0,4 от ОК.
|
|
|
Для получения четкого ответа на вопрос: «За что ставить положительную оценку (и какую) — необходимо решить две задачи:
1) выбрать такую шкалу оценок, в которой доля (%) минимальной положительной оценки от максимальной была бы равна доле знаний и умений экзаменуемого от полных знаний и умений, определяемых рабочей программой дисциплины:
2) давать экзаменуемому задания различных уровней сложности (имеющих разную «стоимость» в баллах), при выполнении которых им набирается сумма баллов, определяющая выставляемую оценку.
Соответствие уровня заданий необходимому объему знаний и умений для их выполнения удобно изображать с помощью графика (рис. 1), на котором по оси ординат отложен уровень знаний и умений экзаменуемого, а по оси абсцисс — уровень сложности задания (Z). При этом величины отрезков, характеризующих сложность задания, прямо пропорциональны его уровню. Для выполнения задания 1-го уровня сложности ОК достаточны пассивные знания понятий, определений, законов, формул; для 2-го уровня OL требуется умение решать простые («типовые») задачи на основании знаний 1-го уровня; 3-ий уровень ОЕ предусматривает умение решать нестандартные задачи.
При умении выполнять задание 2-го уровня хотя бы наполовину (точка N), студент выходит из области пассивных в область активных знаний. Следовательно, линия NP является границей между отрицательными и положительными оценками. Отсюда минимальная доля (R) знаний и умений (от полного знания и умения по данной дисциплине), необходимая для получения положительной оценки, зависит от уровня начальных знаний студента (а). В общем случае, приняв максимальный объем знаний по данной дисциплине за 100%, (BE), можно показать, что
R = (За + 100) / 4(а + 100)
Если (а) может изменяться в широких пределах (от 0 до 90%), то и R изменяется от 25 до 49%. Например, для 1-го курса ХТФ по «Основам теоретической химии» а = 12%, тогда R = 30%. Поэтому при использовании традиционной шкалы оценок, в которой отрицательная оценка «2» от максимальной «5» составляет 40%, она представляется несправедливой, т.к. отрицательная оценка от максимальной должна составлять 30 % (т.е. от 5 баллов — 1,5 балла). При шестибалльной системе — это 2 балла (точнее 1,8), при 24 балльной системе — 7 баллов.
|
|
|
При составлении контрольных заданий удобно «стоимость» задания 1-го уровня оценивать в 1 балл, 2-го — в 2 балла и 3-его — в 3 балла, и число заданий всех трех уровней должно быть одинаковым, чтобы общая сумма баллов была кратна 6. Тогда для получения минимальной положительной оценки студенту необходимо выполнять все задания 1-го уровня и хотя бы наполовину задания 2-го уровня, чтобы набрать сумму баллов, кратную двум и составляющую 1/3 от максимальной суммы баллов.
Для получения хорошей оценки студент должен выполнить задания как 1-го, так и 2-го уровня, т.е. преодолеть границу LQ (рисунок), что соответствует доле знаний и умений R, лежащей в зависимости от величины а в пределах от 43 до 65%. Можно принять R = 62,5%, тогда для получения хорошей оценки по 6-балльной шкале нужно получить 4 балла, по 8-балльной — 5 баллов, а по 24-балльной — 15 баллов.
Для получения отличной оценки студенту необходимо сделать все задания 1-го и 2-го уровней и более чем наполовину задания 3-го уровня — граница ST, что отвечает значениям R от 67 до 82%. Приняв среднее значение R = 74,5%, получаем баллы, необходимые для получения такой оценки: при 6-балльной системе — 5 баллов, при 8-балльной системе — 6 баллов, при 24-балльной системе — 18 баллов.
Для различных учебных дисциплин число уровней сложности заданий должно быть различным. Если для теоретических и расчетных дисциплин составление заданий трех уровней затруднений не вызывает, то для описательных и гуманитарных дисциплин число уровней сложности, по-видимому, снизится до двух. При составлении контрольных заданий различных уровней сложности по каждой теме учебной дисциплины прежде всего требуется установить необходимый минимум знаний для 1-го уровня, а затем указать дополнительные знания, нужные для выполнения заданий 2-го и 3-го уровней.
|
|
|
Пример: тема «Газовые законы»
Минимум знаний:
• 1 моль вещества имеет массу в г, численно равную его молекулярной массе;
• 1 моль газа при н. у. занимает объем 22,4 л;
• формулы распространенных газов.
Дополнительные знания:
умение рассчитать массу вещества по уравнению реакции, умение проводить расчеты по уравнению Клапейрона-Менделеева.
Задание 1-го уровня: найти объем, который занимает при н.у. водород массой 10 г.
Задание 2-го уровня: найти объем при н.у. водорода, выделившегося при растворении в разбавленной серной кислоте 6,6 г цинка.
Задание 3-го уровня: найти объем водорода, выделившегося при растворении в разбавленной серной кислоте 6,5 г цинка при давлении 120 кПа и температуре 40 °С.
Разумеется, в одном экзаменационном билете не должны содержатся задания всех уровней сложности, связанные с одним и тем же объектом, понятием, темой.
Использование предлагаемого подхода к составлению контрольных заданий и оценке знаний студента, по нашему мнению, позволяет повысить ее объективность[6].
|
|
|


