 |
Глава 10 технические измерения фотометрических величин
|
|
|
|
Глава 10 ТЕХНИЧЕСКИЕ ИЗМЕРЕНИЯ ФОТОМЕТРИЧЕСКИХ ВЕЛИЧИН
10. 1. Фотометрия в светотехнике
Самые распространенные технические измерения в светотехнике связаны с определением освещенности на рабочих местах, что является неотъемлемой частью паспортизации предприятий на соответствие принятым нормам [60, 61].
Нормы предусматривают выполнение измерений в определенных плоскостях (уровень рабочего стола, плоскость кульмана или плоскость, касательная к резцу револьверного станка, стена, футбольное поле и т. д. ). При этом расположение источников освещения относительно плоскости измерений является произвольным. Это может быть освещение прямым светом от источников как с узким, так и с широким пространственным распределением светового потока, или освещение отраженным излучением.
Поэтому одним из важнейших моментов выполнения измерений освещенности является точность установки фотометрической головки люксметра в плоскости измерений, т. е. в плоскости, касательной к диффузной насадке ФГ. При установке ФГ на плоскости стола приходится сталкиваться с неопределенностью, зависящей от размера (толщины) ФГ. То же самое происходит при измерении освещенности в плоскости стены. При этом неопределенность (погрешность) измерений будет связана помимо точности прибора с расстоянием между источником освещения и плоскостью измерений. Чем больше расстояние, тем меньше составляющая погрешности, связанная с толщиной ФГ. При расстоянии между плоскостью измерения и источником света, равном 3 м, и толщине ФГ (расстояние от основания корпуса до верхней точки диффузной насадки) — 0, 03 м, погрешность установки ФГ составит 1 %. Эта составляющая погрешности измерений связана только с точностью установки ФГ в требуемой плоскости измерений. Исключить ее можно путем максимального приближения условий установки ФГ люксметра к требованиям норм [60, 61]. Другим примером выполнения рассматриваемых технических измерений служит определение освещенности в плоскости панно в музее. В этом случае плоскость измерений легко находится с учетом расстояния от стены до поверхности картины.
|
|
|
При измерениях освещенности в плоскости рабочего стола (0, 7 м от пола) можно правильно определить плоскость измерений, избежав тем самым дополнительную погрешность технических измерений, связанную с конечными размерами ФГ.
При измерениях же освещенности стены или на ступенях лестничного пролета эта составляющая погрешности остается. Исключить ее можно только при точном знании геометрического фактора, т. е. всех размеров (расстояний) фотометрируемой сцены.
Таким образом, простая процедура технических измерений освещенности, заключающаяся в установке ФР люксметра в заданной плоскости измерений и снятии показаний с дисплейного экрана блока электроники, связана, в первую очередь, с точностью установки ФГ. Погрешность технических измерений в этом случае будет определяться классом точности люксметра, стабильностью источников освещения (СКО результатов измерений) и составляющей погрешности, связанной с правильным определением плоскости измерений и размещением в ней ФГ.
10. 2. Методики выполнения измерений и обработки их результатов с оценками неопределенности
Рассмотрим два примера выполнения измерений в фотометрии, но оценивать будем не погрешность, а неопределенность получаемых результатов с учетом сведений, приведенных в первой части книги [4а, 16].
Пример №■ 1. Измерение прибором непосредственной оценки
Иллюстрируется вклад поправочного множителя, разрешающей способности и возможного дрейфа параметров измерительного прибора в суммарную неопределенность, соответствующую измеряемой величине при определении напряжения на зажимах светоизмерительной лампы.
|
|
|
Методика. Через светоизмерительную лампу протекает постоянный ток JL, и режим ее работы контролируется путем измерения напряжения на контактах лампы VL- Производится 10 повторных отсчетов напряжения VR1 на контактах двухполюсного разъема цифровым вольтметром. После выключения тока по результатам следующих 10 показаний определяется смещающее напряжение VR2- Цифровой вольтметр работает в фиксированном диапазоне измерений с разрешением δ = 0, 0001 В. Результаты измерений представлены в табл. 10. 1.
Первый столбец в таблице, озаглавленный «№», содержит номера 10 измерений. Другие столбцы, озаглавленные VR1 и VR2, соответственно, содержат по 10 результатов измерений двух напряжений и их средние значения, а также стандартные отклонения от среднего, рассчитанные согласно уравнению (1. 1) и зафиксированные в двух нижних строках таблицы.
Принцип измерения. Напряжение лампы VL после измерения на зажимах двухполюсного разъема не является истинным значением, его необходимо скорректировать (1) на значение падения напряжения 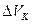 на контактном сопротивлении и (2) на значение термоЭДС
на контактном сопротивлении и (2) на значение термоЭДС 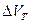 , порожденной градиентом температуры в электрической цепи. Последняя измеряется в отсутствие тока через лампу. В показания цифрового вольтметра вносится поправка, учитывающая напряжение смещения
, порожденной градиентом температуры в электрической цепи. Последняя измеряется в отсутствие тока через лампу. В показания цифрового вольтметра вносится поправка, учитывающая напряжение смещения 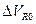 и поправочный множитель cR. Ограниченное разрешение цифрового вольтметра оценивается в отдельности для каждого среднего значения и соответствующего стандартного отклонения:
и поправочный множитель cR. Ограниченное разрешение цифрового вольтметра оценивается в отдельности для каждого среднего значения и соответствующего стандартного отклонения:
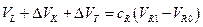 , при
, при 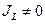 ;
;
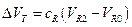 , при
, при 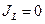 . (10. 1)
. (10. 1)
Модель для определения значения и соответствующей неопределенности выходной величины получена в результате комбинации этих двух уравнений:
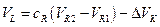 (10. 2)
(10. 2)
Таблица 10. 1. Результаты измерений
| № | Vm | VR2 |
| 25, 0004 | 0, 0022 | |
| 25, 0239 | 0, 0021 | |
| 25, 0063 | 0, 0021 | |
| 25, 0201 | 0, 0021 | |
| 25, 0177 | 0, 0020 | |
| 25, 0185 | 0, 0020 | |
| 25, 0106 | 0, 0021 | |
| 25, 0231 | 0, 0021 | |
| 25, 0067 | 0, 0020 | |
| 25, 0134 | 0, 0021 | |
| Среднее значение | 25, 0141 | 0, 0021 |
| Стандартное отклонение | 0, 00250 | 0, 00001 |
|
|
|
Принятые обозначения:
VL — напряжение на зажимах лампы представляет собой выходную величину, значение которой нужно определить;
 — среднее значение, полученное в результате усреднения n = 10 показаний (см. табл. 10. 1),
— среднее значение, полученное в результате усреднения n = 10 показаний (см. табл. 10. 1), 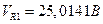 ; стандартное отклонение
; стандартное отклонение  принято равным неопределенности
принято равным неопределенности 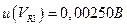 , поскольку оно значительно больше разрешения цифрового вольтметра (δ — 0, 0001 В). Отсюда следует, что в данном случае применима оценка типа А с ограниченным числом степеней свободы
, поскольку оно значительно больше разрешения цифрового вольтметра (δ — 0, 0001 В). Отсюда следует, что в данном случае применима оценка типа А с ограниченным числом степеней свободы 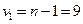 ;
;
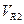 - среднее значение, полученное в результате усреднения n = 10 показаний (см. табл. 10. 1),
- среднее значение, полученное в результате усреднения n = 10 показаний (см. табл. 10. 1), 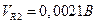 ; разрешение δ = 0, 0001 В (задано с прямоугольным распределением вероятностей) существенно по сравнению со стандартным отклонением
; разрешение δ = 0, 0001 В (задано с прямоугольным распределением вероятностей) существенно по сравнению со стандартным отклонением 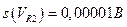 и принято равным неопределенности
и принято равным неопределенности 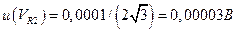 (см. уравнение (1. 6)). Распределение вероятностей при оценке типа В отличается неограниченным числом степеней свободы;
(см. уравнение (1. 6)). Распределение вероятностей при оценке типа В отличается неограниченным числом степеней свободы;
 — поправочный множитель. В сертификате на цифровой вольтметр указан cR = 1, 0000 с соответствующей расширенной неопределенностью, установленной на уровне ± 0, 00050 В ± 6 · 10-5 В от измеренного значения при коэффициенте охвата к = 2. Таким образом, напряжение 25 В определяется с относительной стандартной неопределенностью
— поправочный множитель. В сертификате на цифровой вольтметр указан cR = 1, 0000 с соответствующей расширенной неопределенностью, установленной на уровне ± 0, 00050 В ± 6 · 10-5 В от измеренного значения при коэффициенте охвата к = 2. Таким образом, напряжение 25 В определяется с относительной стандартной неопределенностью  , что тождественно стандартной неопределенности поправочного множителя с распределением вероятностей в соответствии с оценкой типа В и неограниченным числом степеней свободы;
, что тождественно стандартной неопределенности поправочного множителя с распределением вероятностей в соответствии с оценкой типа В и неограниченным числом степеней свободы;
Δ Vk — коррекция падения напряжения на контактном сопротивлении в разъеме, вызванного протеканием тока через лампу; значение и интервал с прямоугольным распределением вероятностей известны из предыдущих экспериментов: 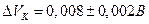 ; неопределенность
; неопределенность 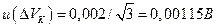 . Распределение вероятностей принятов соответствии с оценкой типа В при неограниченном числе степеней свободы.
. Распределение вероятностей принятов соответствии с оценкой типа В при неограниченном числе степеней свободы.
Коэффициенты чувствительности. Трактовка понятия коэффициентов чувствительности q приведена при рассмотрении уравнения (1. 12). Они рассчитываются согласно модели (10. 2) как частные производные оцениваемой величины. Коэффициенты должны иметь надлежащие знаки даже при том условии, что знак важен только в случае корреляции величин на входе:
|
|
|
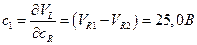 ;
; 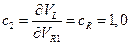 ;
;
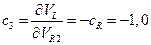 ;
; 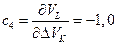 . (10. 3)
. (10. 3)
Суммарная неопределенность выходной величины рассчитывается с учетом вклада входных величин (см. уравнение (1. 12)), которые представляют собой произведения неопределенностей и коэффициентов чувствительности. Эти значения тоже должны иметь надлежащие знаки. В данном случае входные величины некоррелированы, так что суммарная неопределенность выходной величины равна квадратному корню из суммы квадратов отдельных составляющих неопределенности (см. уравнение (1. 13)).
Степени свободы. Состав неопределенностей (табл. 10. 2) показывает, что оценка одной составляющей происходила по типу А с ограниченным числом степеней свободы. В этом случае выражение суммы в формуле Уэлча-Саттертвейта согласно уравнению (1. 19) упрощается и имеет вид
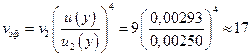 . (10. 4)
. (10. 4)
Расширенная неопределенность: С учетом фактического числа степеней свободы, 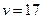 , коэффициент охвата к для вероятности 95, 45 % равен 2, 16, а расширенная неопределенность определяется следующим образом:
, коэффициент охвата к для вероятности 95, 45 % равен 2, 16, а расширенная неопределенность определяется следующим образом: 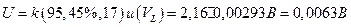 (10. 5)
(10. 5)
Окончательный результат. Напряжение на зажимах лампы VL, равно (25, 0040 ± 0, 0063) В.
Расширенная неопределенность измерения принята равной стандартной
(неопределенности, умноженной на коэффициент охвата к = 2, 16, который для t-распределения с 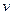 = 17 (число эффективных степеней свободы) соответствует вероятности охвата, приблизительно равной 95 %. Стандартная неопределенность вычисляется согласно «Руководству по выражению неопределенностей измерений» [15].
= 17 (число эффективных степеней свободы) соответствует вероятности охвата, приблизительно равной 95 %. Стандартная неопределенность вычисляется согласно «Руководству по выражению неопределенностей измерений» [15].
Пример № 2. Измерение освещенности фотометром Измерение освещенности на приемной площадке измерительного преобразователя фотометра.
Методика. Источник света с известной температурой распределения равномерно освещает приемную площадку термостатированного И Π фотометра в направлении нормального падения луча с достаточно большого расстояния, так что по сравнению с этим расстоянием размерами лампы и ИП можно пренебречь. В запрограммированном режиме фотометр регистрирует среднее Tab лица 1U. 2. Составляющие неопределенности значение фототока и соответствующее стандартное отклонение, вычисленные по 30 показаниям. Перед измерением сдвиг нуля прибора был устранен.
| № | Входное воздействие Хг | Символ | Значение Xj | Стандартная неопределенность и | Тип оценки | Число степеней свободы V | Коэффициент чувствительности Cj | Вклад в неопределенность Щ{у)М |
| Калибровка | CR | 1, 0000 | 0, 00004 | В | оо | 25, 0 В | 0, 00100 | |
| Напряжение | Vm | 25, 0141 В | 0, 00250 В | А | 1, 0 | 0, 00250 | ||
| Терм, сдвиг | VR2 | 0, 00210 В | 0, 00003 В | В | оо | -1, 0 | -0, 00003 | |
| Поправка | 0, 00800 В | 0, 00115 В | В | оо | -1, 0 | -0, 00115 | ||
| Напряжение лампы | Vl | 25, 0040 В | 0, 00293 |
|
|
|
Результаты измерений. Аналогично предыдущим примерам, определяются по 30 показаниям среднее значение V = 20, 546 нА и соответствующее стандартное отклонение s(V) = 0, 056 нА. Источником излучения служит лампа с температурой распределения Тд = 2800 К, известной в пределах интервала ± 30 К с прямоугольным распределением вероятностей. Разрешение измерителя (0, 001 нА) пренебрежимо мало по сравнению со стандартным отклонением сигнала.
Принцип измерения. Излучение точечного источника перезаполняет приемную площадку ИП, а его поток центрирован по отношению к ней и падает под углом ε к нормали. При этом генерируется фототок V. Эффективная поверхность представляет собой проекцию приемной площадки, изменяющуюся по косинусоидальному закону в зависимости от ε. Световая чувствительность sv соответствует источнику света А (температура распределения ТD = = 2856 К), а ее значение и неопределенность известны из сертификата фотометра. Это позволяет рассчитать освещенность Ε (ТD)- Фотометрическая головка скорректирована по  , и есть возможность внести поправку на рассогласование со спектральной характеристикой ИП с помощью отношения температур распределения ТD и ТA с показателем степени рассогласования m. На уровень фототока оказывает влияние рассеянное световое излучение. Его относительный вклад обозначается как cstray. Изменение окружающей температуры Δ Τ не влияет на спектральную характеристику благодаря температурной стабилизация фотометрической головки, но показания прибора меняются в соответствии с коэффициентом са:
, и есть возможность внести поправку на рассогласование со спектральной характеристикой ИП с помощью отношения температур распределения ТD и ТA с показателем степени рассогласования m. На уровень фототока оказывает влияние рассеянное световое излучение. Его относительный вклад обозначается как cstray. Изменение окружающей температуры Δ Τ не влияет на спектральную характеристику благодаря температурной стабилизация фотометрической головки, но показания прибора меняются в соответствии с коэффициентом са:
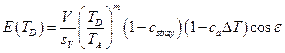 (10. 6)
(10. 6)
Поскольку все поправки незначительны, в качестве модели оценки можно использовать упрощенное уравнение:
Модель. (10. 7)
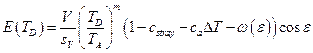 (10. 7)
(10. 7)
Принятые обозначения: 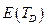 — выходная величина, освещенность приемной площадки;
— выходная величина, освещенность приемной площадки;
V — среднее значение, полученное в результате усреднения 30 показаний; V = 20, 546 нА; стандартное отклонение s(V) принято равным стандартной неопределенности u(V) = 0, 056 нА;
sV — световая чувствительность фотометра, указанная в сертификате на уровне значимости к = 2, sV = 2, 673 нА/лк. Относительная расширенная неопределенность равна 0, 0062, а стандартная неопределенность 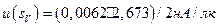 ;
;
m — показатель степени рассогласования m = 0, 02. Определяется с помощью эталонного фотометра, оценивается в интервале ±0, 01 с прямоугольным распределением вероятностей. Стандартная неопределенность 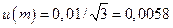 ;
;
 — температура распределения
— температура распределения 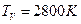 в интервале ± 30 К с прямоугольным распределением вероятностей. Стандартная неопределенность
в интервале ± 30 К с прямоугольным распределением вероятностей. Стандартная неопределенность 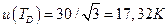 ;
;
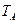 — эталонная температура распределения
— эталонная температура распределения 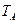 = 2856K, неопределенность не задается;
= 2856K, неопределенность не задается;
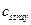 - относительная поправка на рассеянное световое излучение;
- относительная поправка на рассеянное световое излучение; 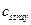 = 0, 0004 определяется по результатам предыдущих измерений и оценивается в интервале ±0, 0002 с прямоугольным распределением вероятностей. Стандартная неопределенность
= 0, 0004 определяется по результатам предыдущих измерений и оценивается в интервале ±0, 0002 с прямоугольным распределением вероятностей. Стандартная неопределенность 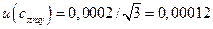 ;
; 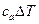 — относительная поправка, учитывающая влияние изменения окружающей температуры. Стабилизация с помощью системы кондиционирования воздуха сводит к нулю это произведение в интервале ± 0, 0007 с прямоугольным распределением вероятностей. Стандартная неопределенность
— относительная поправка, учитывающая влияние изменения окружающей температуры. Стабилизация с помощью системы кондиционирования воздуха сводит к нулю это произведение в интервале ± 0, 0007 с прямоугольным распределением вероятностей. Стандартная неопределенность 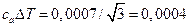 ;
;
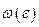 — угловое рассогласование в интервале
— угловое рассогласование в интервале 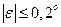 с прямоугольным распределением вероятностей. Поправка не вводится. Неопределенность рассчитывается по уравнению (1. 10): (0, 2 · π /180) 2/л/З = 0, 00002. Коэффициенты чувствительности. Они рассчитываются, исходя из модели, соответствующей уравнению (10. 2), как частные производные оцениваемой величины. Эти коэффициенты должны быть представлены с надлежащим знаком, что особенно важно при наличии корреляции входных величин:
с прямоугольным распределением вероятностей. Поправка не вводится. Неопределенность рассчитывается по уравнению (1. 10): (0, 2 · π /180) 2/л/З = 0, 00002. Коэффициенты чувствительности. Они рассчитываются, исходя из модели, соответствующей уравнению (10. 2), как частные производные оцениваемой величины. Эти коэффициенты должны быть представлены с надлежащим знаком, что особенно важно при наличии корреляции входных величин:
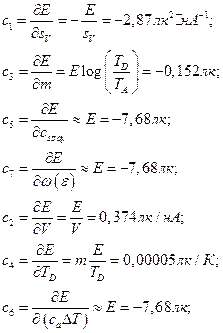 (10. 8)
(10. 8)
Суммарная неопределенность выходной величины рассчитывается аналогично примеру 1.
Составляющие неопределенности приведены в табл. 10. 3.
 Таблица 10. 3. Составляющие неопределенности
Таблица 10. 3. Составляющие неопределенности
| Входное воздействие Xt | Обозначение | Значение Xi | Стандартная неопределенность u{xi) | Тип оценки | Число степеней свободы υ. | Коэффициент чувствительности d | Вклад в неопределенность щ(у)/лк |
| Чувствительность | sv | 2, 673 нА/лк | 0, 00829 нА/лк | В | оо | -2, 87 лк2/нА | -0, 02382 |
| Показание | V | 20, 546 нА | 0, 056 нА | А | 0, 374 лк/нА | +0, 02093 | |
| Рассогласование | т | 0, 02 | 0, 0058 | В | оо | -0, 152 лк | -0, 00088 |
| Температурное распределение | TD | 2800 К | 17, 32 К | В | оо | 0, 00005 лк/К | 0, 00095 |
| Поправка на рассеянное излучение | Cstray | 0, 0004 | 0, 00012 | В | . ОО | -7, 68 лк | -0, 00092 |
| Поправка на окружающую температуру | 0, 0 | 0, 0004 | В | оо | -7, 68 лк | -0, 00307 | |
| Угловое рассо-глосование | w{e) | 0, 0 | 0, 00002 | В | -7, 68 лк | -0, 00015 | |
| Освещенность | Е(То) | 7, 68041 лк | > 100 | 0, 03190 |
Модель. 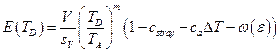 .
.
Степени свободы. Среди составляющих неопределенности есть лишь одна с оценкой по типу А с 9 степенями свободы, что позволяет упростить выражение суммы в формуле Уэлча-Саттертвейта в уравнении (1. 19):
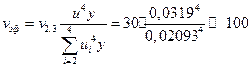 (10. 9)
(10. 9)
Расширенная неопределенность. Коэффициент охвата, для вероятности 95, 45 %, к = 2. Расширенная неопределенность вычисляется из выражения
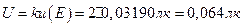 (10. 10)
(10. 10)
Окончательный результат. Измеренная фотометром освещенность составляет (7, 680 ± 0, 064) лк.
Расширенная неопределенность измерения принята равной стандартной неопределенности, умноженной на коэффициент охвата к = 2, который соответствует вероятности охвата, приблизительно равной 95 %. Стандартная неопределенность вычисляется согласно «Руководству по выражению неопределенности измерений» [15].
|
|
|


