17.5. Методика и пример выполнения эталонных измерений и обработки их результатов с оценкой неопределенности

В двух предыдущих параграфах точность эталонных измерений оценива­лась значением суммарной погрешности каждого из двух РЭ. Покажем на примере, как выглядят методика и результаты калибровки разрядного эта­лона единицы мощности лазерного излучения (именуемого кали5руемым из­мерителем мощности) по более точному эталону с оценкой неопределенности измерения [4 а, 16]. Влияние внешних факторов (окружающей температуры, рассеянного светового излучения и т. д. ) не учитывается.

 

Таблица 17. 11. Определение Sn

№№ точек спектральн. и динамич. диапазона	λ, мкм	Q, мДж	σ ι, %	σ ι, %	Sn, %
	1, 06	153, 97	0, 341	0, 194	0, 3923
	1, 06	62, 68	0, 338	0, 283	0, 4408
	1, 06	6, 82	0, 279	0, 396	0, 4844
	0, 53	41, 42	0, 164	0, 178	0, 2420
	0, 53	2, 90	0, 134	0, 145	0, 1974
	1, 54	106, 2	0, 115	0, 231	0, 4034
	1, 54	54, 95	0, 186	0, 358	0, 2580
	1, 54		0, 064	0, 314	0, 3205

Методика. Лазерный луч является источником излучения при опреде­лении поправочного множителя при калибровке измерителя мощности по аналогичному прибору, использованному в качестве эталона. Два первичных измерительных преобразователя этих приборов облучаются поочередно лучом стабилизированного (по длине волны и мощности) лазера. Луч полностью вписывается во входные апертуры, съюстированые в плоскости нормального угла падения пучка. При облучении одного ИП другой экранируется, и при этом измеряются сигнал и сдвиг нулевого уровня соответственно. После того, как ИП меняются местами, снимаются еще два показания. Эта процедура по­вторяется 10 раз и результаты измерений сводятся в таблицу. Оба измерителя мощности работают в фиксированных диапазонах измерений. Результаты измерений представлены в табл. 17. 12.

Первый столбец табл. 17. 12 содержит номера 10 измерений. Значения фо­тотока сигнала и сдвига нуля калибруемого измерителя приведены в столбцах V1 и Vo соответственно, а разности V1 — V0 — в столбце V10. В столбцах  и  представлены соответствующие значения фототока и сдвига нуля эта­лонного измерителя. В нижние графы табл. 17. 12 сведены средние значения и соответствующие стандартные отклонения от среднего (см. уравнение (1. 1)), а в последнюю графу — коэффициенты корреляции согласно уравнению (1. 3) для сигнала и сдвига нуля обоих измерителей.

Принцип измерения. Лазер, работающий на фиксированной длине вол­ны, например, , с мощностью выходного излучения 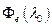, равной 1 мВт, используется для передачи значения поправочного множителя c_R от эталонного измерителя калибруемому прибору. Поскольку оба И Π не могут облучаться одновременно, любой дрейф или шум лазера или измерительных приборов приводит к увеличению стандартной неопределенности поправочно­го множителя. Приведенные в таблице значения выходного сигнала и сдвига нуля эталонного измерителя стабильны и имеют очень малый коэффициент корреляции, что свидетельствует о высокой стабильности источника излуче­ния. Показания калибруемого прибора демонстрируют значительный дрейф сдвига нуля (вероятно, из-за влияния температуры) и сильно коррелируют со значениями выходного сигнала. Влияние корреляции компенсируется, ес­ли различия сигнала и сдвига нуля в столбце V10 усреднить. Поправочный множитель с калибруемого измерителя рассчитывается исходя из показаний обоих приборов с учетом поправочного множителя  эталонного измерителя при условии использования некоррелированных входных величин:

                                 (17. 46)

Таблица 17. 12. Результаты измерений

№	Vi	Vo		Vm	Vro
	мка	мка	мка	мка	мка
	25, 057	0, 002	25, 055	17, 9681	0, 0058
	25, 100	0, 034	25, 066	18, 0155	0, 0124
	25, 117	0, 066	25, 051	17, 9707	0, 0122
	25, 066	0, 070	24, 996	18, 0369	0, 0094
	25, 078	0, 112	24, 966	17, 9542	0, 0102
	25, 097	0, 096	25, 001	17, 9721	0, 0144
	25, 163	0, 142	25, 021	17, 9463	0, 0060
	25, 196	0, 175	25, 021	17, 9521	0, 0148
	25, 112	0, 191	24, 921	17, 9921	0, 0081
	25, 254	0, 210	25, 044	17, 9661	0, 0138
Среднее знач.	25, 1240	0, 1098	25, 0142	17, 9774	0, 0107
Станд. откл.	0, 01974	0, 02185	0, 01422	0, 00921	0, 00105
Коэффициент корреляции	0, 77084			-0, 01816

 

Поправочный множитель калибруемого измерителя можно найти с по­мощью модели для определения измеряемого значения и соответствую­щей неопределенности. Разрешающие способности обоих измерителей (δ = = 0, 001 мкА у калибруемого и 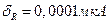— у эталонного измерителя) крайне незначительны и не влияют на стандартные отклонения измеренных значений.

Модель:

                                          (17. 47)

Принятые обозначения: с — выходная величина, поправочный мно­житель для калибруемого измерителя мощности; c_R — поправочный множи­тель эталонного измерителя мощности, приведенный в сертификате, c_R = = 12, 543 мкА/Вт. Соответствующая расширенная неопределенность равна 0, 0043 при коэффициенте охвата к = 2. Эти данные преобразуются в стандарт­ную неопределенность согласно оценке типа В, = (0, 0043 · 12, 543/2 = = 0, 0270) мкА/Вт, с известным распределением вероятностей при неограни­ченном числе степеней свободы;

— среднее значение, полученное путем усреднения n = 10 отсчетов в табл. 17. 12,  = 17, 9774 мкА; стандартное отклонение  принято равным стандартной неопределенности = 0, 00921 мкА, поскольку оно значительно больше разрешения. Отсюда следует, что в данном случае умест­на оценка типа А с числом степеней свободы ν = 9; — среднее значение, полученное путем усреднения n = 10 отсчетов в табл. 17. 12, Vrq = 0, 0107 мкА; стандартное отклонение  принято равным стандартной неопределенно­сти  = 0, 00105 мкА, поскольку оно значительно больше разрешения. Отсюда следует, что в данном случае применима оценка типа А с числом степеней свободы v = 9;

— среднее значение, полученное путем усреднения n = 10 разностей показаний, = 25, 0142 мкА; стандартное отклонение  принято рав­ным стандартной неопределенности 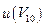 = 0, 01422 мкА, а корреляция не учитывается. Эти значения соответствует оценке типа А с числом степеней свободы ν = 9.

Коэффициенты чувствительности. Суть коэффициентов чувстви­тельности c_i понятна из уравнения (1. 12). Они рассчитываются, исходя из модели, соответствующей уравнению (10. 5), как частные производные оцени­ваемой величины. Эти коэффициенты должны быть представлены с надлежа­щим знаком, что особенно важно при наличии корреляции входных величин:

                                   (17. 48)

Суммарная неопределенность выходной величины рассчитывается' соглас­но примерам в параграфе 10. 4. Составляющие неопределенности приведены в табл. 17. 13.

 

Таблица 17. 13. Составляющие неопределенности

	Входное воз­действие Xi	Обоз­наче­ние	Значе­ние Xi	Стандарт­ная неопре­делен­ность u( Xi)	Тип оцен­ки	Число степеней свободы Щ	Коэффици­ент чув­ствитель­ности с, -	Вклад неопре­деленность щ{у)1 [мкА/Вт]
	Калибровка	CR	12, 543 мкА/Вт	0, 0270 мкА/Вт	В	со	0, 718	0, 0194
	Фототек	VRX	17, 9774 мкА	0, 00921 мкА	А		0, 501 Вт" 1	0, 0046
	Сдвиг нуля	Vro	0, 0107 мкА	0, 00105 мкА	А		-0, 501 Вт" 1	-0, 0005
	Разность токов		25, 0142 мкА	0, 01422 мкА	А		-0, 360 Вт-1	-0, 0051
	Поправоч­ный множитель	С	9, 0091 мкА/Вт			> 100		0, 0206

Модель:

Степени свободы. Состав неопределенностей показывает, что имеются 3 составляющих (оценка типа А), все с 9 степенями свободы. Это позволяяет упростить выражение суммы в формуле Уэлча-Саттертвейта в уравне­нии (1. 19):

                      (17. 49)

Расширенная неопределенность. Благодаря большому числу степе­ней свободы, коэффициент охвата для вероятности 95, 45 % к = 2. Поэтому расширенная неопределенность определяется из выражения

(17. 50)

Окончательный результат. Поправочный множитель для калибруемо­го измерителя мощности, определенный для мощности излучения, приблизи­тельно равной 1 мВт при длине волны 633 нм, составил (9, 009 ± 0, 041) мкА/Вт.

Расширенная неопределенность измерения принята равной стандартной неопределенности, умноженной на коэффициент охвата А; = 2, который со­ответствует вероятности охвата, приблизительно равной 95%. Стандартная неопределенность вычисляется согласно «Руководству по выражению неопре­деленности измерений» [15].

⇐ Предыдущая59606162636465666768Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: