 |
Глава 18 измерения пространственно-энергетических параметров и характеристик лазерного излучения
|
|
|
|
Глава 18 ИЗМЕРЕНИЯ ПРОСТРАНСТВЕННО-ЭНЕРГЕТИЧЕСКИХ ПАРАМЕТРОВ И ХАРАКТЕРИСТИК ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
В последнее десятилетие значительно усилились тенденции разработчиков и изготовителей лазеров· и лазерных устройств, направленные на обеспечение по возможности равномерного распределения плотности мощности (энергии) в поперечном сечении пучка лазерного излучения. Наряду со стремлением к получению пучка с сечением в виде однородной плоской вершины («шляпы») наблюдается желание максимально приблизить распределение плотности к гауссову. Ученые, инженеры, технологи обнаружили, что во многих применениях лазерной техники требуется весьма высокая однородность распределения интенсивности в сечении пучка. Особенно актуализировались эти требования по мере совершенствования измерительной аппаратуры, позволявшей определять ранее не доступные для измерения пространственно-энергетические параметры и характеристики лазерного излучения.
Однако проблема улучшения качества лазерного пучка продолжает существовать, особенно для многомодовых лазеров. Поэтому наличие доступной, автоматизированной, несложной в эксплуатации измерительной аппаратуры полезно не только пользователю, но и изготовителю лазера, ибо помогает в настройке и сертификации излучателя.
Современная электроника и вычислительная техника открыли возможности и создали предпосылки для создания многопараметровых, в реальном масштабе времени, с наглядным отображением достаточно точных результатов измерений, устройств на базе серийных камер, микропроцессоров, дисплеев и др. атрибутов оптико-электронного приборостроения.
Подобные измерительные устройства особенно полезны в ситуациях, когда необходим непрерывный или периодический контроль стабильности параметров и характеристик распространения пучка лазерного излучения, поскольку имеется достаточное количество дестабилизирующих факторов: тепловой дрейф, старение и нестабильность компонентов активного элемента, вибрация и удары по резонатору, помутнение оптических элементов и оседающая на их поверхностях пыль и грязь, а также царапины, разъюстировка оптического тракта, ухудшение качества, нелинейность и неоднородность активной среды и пр. Поэтому далее остановимся на основных стандартизованных терминах и определениях, алгоритмах измерений, наиболее современных РСИ пространственно-энергетических параметров и характеристик лазерного излучения, а также на метрологических аспектах этого подвида измерений.
|
|
|
18. 1. Основы измерений
18. 1. 1. Основные термины, определения и соотношения. Основополагающим для этого направления измерений документом служит Международный Стандарт ИСО 11146 [88].
Во введении к стандарту пучки лазерного излучения делятся на три вида: радиально-симметричные, радиально-несимметричные, астигматичные (скрученные или изогнутые). Стандарт [88] не распространяется на пучки третьего вида.
Любой радиально-симметричный пучок лазерного излучения описывается тремя параметрами:
· местоположением перетяжки пучка z0;
· диаметром пучка в перетяжке 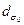 ,
,
· углом расходимости пучка 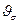 дальней зоне.
дальней зоне.
Примечание. Перетяжкой пучка именуется его сечение с минимальными поперечными размерами.
Зная эти три параметра, можно для углов расходимости менее 0, 8 рад записать в первом приближении уравнение распространения пучка вдоль его оси z
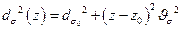 (18. 1)
(18. 1)
где z0— расстояние, на которое удалено от начала оси zместоположение перетяжки; обычно начало оси zрасположено в опорной плоскости х-у, совпадающей, например, с передней торцевой поверхностью корпуса лазера.
|
|
|
Уравнение (18. 1) справедливо при условии, что для определения поперечного размера (ширины) и расходимости пучка используются моменты второго порядка функции распределения плотности мощности (энергии) в его поперечном сечении.
Качество пучка в процессе его распространения отныне предложено характеризовать показателем (коэффициентом) К распространения пучка или обратной ему величиной М2, являющейся мерой близости произведения параметров измеряемого пучка к аналогичному произведению для идеального гауссова пучка.
В результате появилось расхожее выражение «критерий М2», причем у гауссова пучка с одной модой ТЕМ00 значение М2 = 1.
Величины К (или Μ 2), 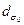
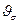 связывает выражение
связывает выражение
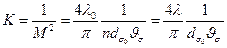 (18. 2)
(18. 2)
где λ ο — длина волны излучения в вакууме; 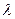 — длина волны излучения в среде с показателем преломления п.
— длина волны излучения в среде с показателем преломления п.
При этом считается, что К достаточно измерять с погрешностью порядка 10%, хотя при 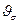 > 0, 8 рад погрешности могут оказаться существенно большими.
> 0, 8 рад погрешности могут оказаться существенно большими.
Произведение
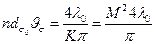 (18. 3)
(18. 3)
является инвариантом распространения пучка лазерного излучения в безаберрационной среде в отсутствие ограничивающих его диафрагм.
Для описания радиально-несимметричных пучков необходимы семь параметров:
· местоположения перетяжек пучка 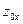 и
и 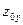 .
.
· поперечные размеры (ширины) пучка 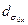 и
и 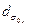 ;
;
· углы расходимости пучка в дальней зоне 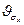 и
и 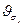 ;
;
· азимутальный угол  между осью xпучка и осью х1 лабораторной системы координат.
между осью xпучка и осью х1 лабораторной системы координат.
По аналогии с уравнением (18. 3) инвариант распространения радиально-несимметричного пучка записывается в виде двух независимых выражений для каждой из ортогональных осей χ и у с использованием либо Кх и Ку, либо  и
и 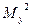 -
-
В стандарте [88] для определения поперечного размера (ширины) пучка необходимо измерить распределение плотности мощности (энергии) в его поперечном сечении и вычислить моменты второго порядка полученной функции. Поскольку далеко не всегда такое распределение может быть аппроксимировано аналитической функцией, или же затруднено использование прямого измерения распределения плотности, стандартом предусмотрены три альтернативных метода измерений поперечных размеров пучков:
|
|
|
· варьируемой диафрагмы;
· движущегося острого края (лезвия ножа);
· изменяющейся по ширине щели.
Как следует из вышеизложенного, для дальнейшего рассмотрения необходимо привести ряд стандартизованных терминов и определений [88].
Плотностью энергии Н(х, у) считается часть энергии в поперечном сечении пучка, приходящаяся на элементарную площадку δ А с координатами х, у и отнесенная к δ А.
Плотностью мощности Е(х, у) считается часть мощности в поперечном сечении пучка, приходящаяся на элементарную площадку δ А с координатами ж, у и отнесенная к δ А.
Местоположения перетяжек пучка z0(радиально-симметричного), zox, zoy (радиально-несимметричного) — точки на оси zраспространения пучка, где его ширина (поперечный размер) минимальна.
Примечание. См. формулу (18. 1).
Диаметр пучка 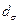 определен для радиально-симметричного пучка, причем
определен для радиально-симметричного пучка, причем
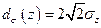 (18. 4)
(18. 4)
где момент второго порядка функции распределения плотности мощности Е(х, у, z)в сечении пучка с координатой zописывается выражением
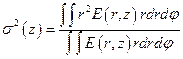 (18. 5)
(18. 5)
где г — расстояние до центра тяжести сечения 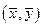 , а координаты
, а координаты 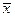 и
и 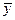 , являющиеся моментами первого порядка, вычисляются по формулам
, являющиеся моментами первого порядка, вычисляются по формулам
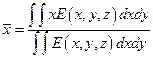 (18. 6)
(18. 6)
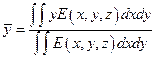 (18. 7)
(18. 7)
Ширины пучков 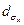 и
и 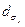 определены для радиальнонесимметричных пучков, причем
определены для радиальнонесимметричных пучков, причем
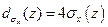 (18. 8)
(18. 8)
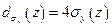 (18. 9)
(18. 9)
где моменты второго порядка функции распределения плотности мощности Е(х, у, z) в сечении пучка с координатой z описываются следующими выражениями:
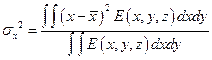 (18. 10)
(18. 10)
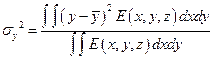 (18. 11)
(18. 11)
где 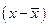 и
и 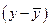 — расстояния до центра тяжести (
— расстояния до центра тяжести ( 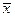 ,
, 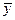 ). Координаты
). Координаты 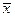 н
н 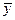 , являющиеся моментами первого порядка, вычисляются по формулам (18. 6) и (18. 7).
, являющиеся моментами первого порядка, вычисляются по формулам (18. 6) и (18. 7).
Примечание. Все приведенные выше соотношения справедливы при замене Е(х, у, z) на Н(х, у, z).
|
|
|
Коэффициент превышения дифракционного предела, присущего идеальному гауссову пучку,
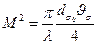 (18. 12)
(18. 12)
Именно этот «критерий М2» принято считать характеристикой «ухудшения» качества реального пучка лазерного излучения по сравнению с идеальным, обладающим чисто дифракционной расходимостью, у которого, как упоминалось ранее, М2 = 1.
Поясним это более наглядно [89], обратившись к рис. 18. 1 и формуле (18. 1).
Отметим, что формула (18. 1) справедлива для любого параксиального пучка и не базируется ни на Лагерра-Гаусса, ни на Эрмита-Гаусса аппроксимациях распределения поля излучения. Она сводится к уравнению распространения, вытекающему из теории гауссовых пучков. Реальный пучок, даже если он представляется предельно «гауссоподобным», принципиально не может достичь идеала с М2 = 1, так как выходное отверстие лазера ограничено и неизбежно отсекаются моды высших порядков, излучаемые по периферии сечения пучка. Есть и ряд других факторов, подавляющих излучение более высоких дифракционных порядков и тем самым искажающих теоретически идеальную сферическую форму волнового фронта. (Стремление к достижению М2 = 1 аналогично попытке приблизиться к нулевой температуре по шкале Кельвина). Для гауссова пучка (М2 = 1) справедлив фундаментальный
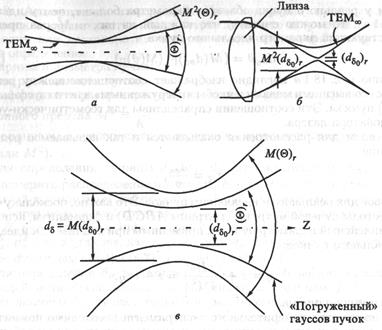
Рис. 18. 1. Иллюстрация соотношений между идеальным и реальным пучками ■ предел:
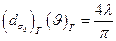 (18. 13)
(18. 13)
где 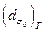 и
и 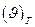 — диаметр в перетяжке и угол расходимости гауссова пучка, соответственно; λ — длина волны лазерного излучения.
— диаметр в перетяжке и угол расходимости гауссова пучка, соответственно; λ — длина волны лазерного излучения.
У реальных пучков произведение диаметра (или ширины) пучка в перетяжке и угла расходимости больше фундаментального предела в М2 раз, т. е.
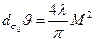 (18. 14 а)
(18. 14 а)
Различные варианты выражения (18. 14 a) отображены на рис. 18. 1, что позволяет лучше уяснить смысл критерия М2.
Если идеальный (гауссов) и реальный пучки имеют одинаковые диаметры 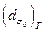 перетяжки, но разные расходимости (рис. 18. 1 a), то у реального пучка угол расходимости в М2 раз больше, чем у идеального, т. е.
перетяжки, но разные расходимости (рис. 18. 1 a), то у реального пучка угол расходимости в М2 раз больше, чем у идеального, т. е.
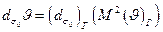 (18. 14 6)
(18. 14 6)
Если оба пучка имеют одинаковые углы расходимости 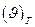 , но разные диаметры перетяжки (рис. 18. 1 5), то у реального пучка этот диаметр будет в М2 раз больше, чем у идеального, т. е.
, но разные диаметры перетяжки (рис. 18. 1 5), то у реального пучка этот диаметр будет в М2 раз больше, чем у идеального, т. е.
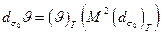 (18. 14 в)
(18. 14 в)
Если у реального пучка оба этих параметра больше, чем у идеального (рис. 18. 1 в), то можно считать, что каждый из них в Μ раз превышает соответствующий параметр идеального пучка, т. е.
|
|
|
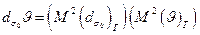 (18. 14 г)
(18. 14 г)
Именно рис. 18. 1 в наглядно изображает соотношение между реальным пучком с его высшими модами и якобы «погруженным» в него гауссовым (идеальным) пучком. Эти соотношения справедливы для геометрически-устойчивого резонатора лазера.
Полезным для рассмотрения оказывается и так называемое рэлеевское расстояние
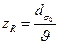 (18. 15)
(18. 15)
одинаковое для реального и идеального пучков. Это важно, поскольку означает, что методы лучевой матрицы (матрицы ABCD) и формализм, использующий комплексный параметр пучка q, применимы при анализе как идеального, так и реального пучков:
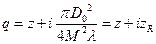 (18. 16)
(18. 16)
где i — мнимая единица.
При постановке измерительного эксперимента необходимо помнить о системе координат, поскольку между системами координат пучка и лаборатории может существовать различие. Координаты х, у и z определяют взаимно ортогональные оси декартовой системы координат пучка. Оси χ и у расположены в плоскости, перпендикулярной пучку, распространяющемуся в направлении оси z. Начало координат этой системы находится в опорной плоскости, сертифицируемой изготовителем лазера (например, в плоскости переднего торца корпуса лазерного устройства). Для пучков с сечением в форме эллипса главные плоскости распространения, обозначаемые как χ -z и y-z, содержат соответственно большую и малую оси эллипса.
В принципе главные плоскости распространения излучения не совпадают с плоскостями x'-z, y'-z лабораторной системы координат x't yr, z, поэтому приходится выбирать одну из двух эквивалентных методик:
· если азимутальный угол φ системы координат пучка относительно системы х', у', z известен, то параметры пучка могут быть измерены непосредственно в системе х, у, z, а угол φ при этом зарегистрирован в процессе измерений;
· если направленности главных осей пучка не известны, они могут быть определены путем измерений двух моментов второго порядка 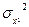 ,
, 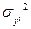 и смешанного момента
и смешанного момента 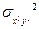 функции распределения плотности мощности или энергии в лабораторной системе координат; это позволит вычислить
функции распределения плотности мощности или энергии в лабораторной системе координат; это позволит вычислить 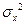 ,
, 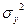 и угол
и угол  между двумя системами, причем
между двумя системами, причем
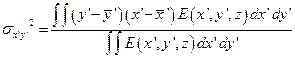 (18. 17)
(18. 17)
18. 1. 2. Алгоритмы измерений. При измерении пространственно-энергетических характеристик и параметров лазерного излучения приходится решать одну или несколько из четырех типичных измерительных задач, а именно определения:
1) ширины и диаметра пучка;
2) угла расходимости пучка;
3) коэффициента распространения К или коэффициента превышения дифракционного предела 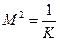 ;
;
4) координаты z0 расположения перетяжки пучка в сочетании с 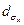 ,
, 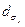 ,
,
1. 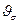 , Κ (или М2).
, Κ (или М2).
1. Для определения ширины 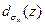 ,
, 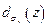 или диаметра
или диаметра 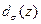 пучка следует измерить распределение плотности Ε или Η в сечении пучка x', у' с координатой z и при этом найти угол φ. После аппроксимации полученного распределения подходящей функцией, следует вычислить моменты первого порядка
пучка следует измерить распределение плотности Ε или Η в сечении пучка x', у' с координатой z и при этом найти угол φ. После аппроксимации полученного распределения подходящей функцией, следует вычислить моменты первого порядка 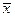 ,
, 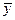 , содержащие информацию о системе координат х, у, z, а затем найти
, содержащие информацию о системе координат х, у, z, а затем найти 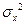 ,
, 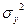 или σ 2 так же, как
или σ 2 так же, как 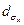 , day или
, day или 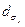 . Вычисления следует производить по формулам (18. 4)—(18. 7), а также (18. 8)—(18. 11).
. Вычисления следует производить по формулам (18. 4)—(18. 7), а также (18. 8)—(18. 11).
2. Для определения 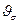 необходимо использовать безаберрационный фокусирующий оптический элемент с фокусным расстоянием f. Измерению подлежит диаметр
необходимо использовать безаберрационный фокусирующий оптический элемент с фокусным расстоянием f. Измерению подлежит диаметр 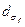 ; пучка в точке оси, расположенной на расстоянии f от задней главной плоскости фокусирующего элемента. Тогда угол расходимости лазерного пучка до его вхождения в оптический элемент рассчитывается по формуле
; пучка в точке оси, расположенной на расстоянии f от задней главной плоскости фокусирующего элемента. Тогда угол расходимости лазерного пучка до его вхождения в оптический элемент рассчитывается по формуле
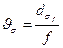 (18. 18)
(18. 18)
Для радиально-несимметричных пучков углы расходимости 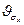 или
или 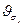 в плоскостях x-y или y-z определяются не по диаметру, а по ширинам пучков.
в плоскостях x-y или y-z определяются не по диаметру, а по ширинам пучков.
3. Для определения Кх, Ку или К и, соответственно,  ,
, 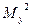 или М2 необходимо найти ширины перетяжек
или М2 необходимо найти ширины перетяжек 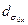 ,
, 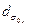 или диаметр перетяжки
или диаметр перетяжки 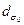 и углы расходимости
и углы расходимости 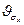 ,
, 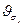 или
или 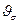 .
.
4. Для определения координаты z расположения перетяжки пучка, а также измерения ширин пучка вдоль осей x и у в том же сечении, необходимо учитывать параметры распространения излучения по трассе пучка (вдоль оси z) и использовать аппроксимирующие формулы, зависящие от степени его радиальной симметрии.
18. 1. 3. Подготовка к измерениям и выбор элементов измерительной аппаратуры. Измерения всех перечисленных параметров базируются на определении функции распределения плотности мощности (энергии) в поперечном сечении пучка выходного лазерного излучения (т. е. вне резонатора лазера).
Подготовка к измерениям начинается с юстировки измерительной установки, ось которой должна быть коаксиальна измеряемому пучку. Для юстировки обычно пользуются вспомогательными лазерами (чаще всего гелий-неоновыми с длиной волны 0, 6328 мкм) и отклоняющими зеркалами. Апертура оптической системы должна вмещать (охватывать) сечение пучка таким образом, чтобы его непопадание (т. е. отсекаемая часть) по мощности (энергии) не превосходило 1 % от суммарного измеряемого значения. Ослабители и формирующие оптические элементы должны быть смонтированы таким образом, чтобы оптическая ось проходила через их центры. Во избежание появления систематических погрешностей необходимо предельно минимизировать влияние отражений, интерференционных эффектов, внешних засветок, тепловых и конвективных воздушных потоков.
После завершения всех перечисленных приготовлений необходимо убедиться в том, что измеряемый пучок достигает приемной площадки ОЭИП. С этой целью перед каждым элементом оптической трассы измерительной установки в пучок вводятся поочередно диафрагмы разных диаметров. Диафрагма, уменьшающая выходной сигнал на 5 %, должна иметь диаметр мень-: ший, чем 0, 8 апертуры оптического элемента.
Для уменьшения возможных дополнительных погрешностей необходимо принять меры по вибро- и акустической защите установки, ее экранированию от электромагнитных излучений, термостабилизации лаборатории, выбору малошумящих усилителей и пр. В случае измерения пространственно-энергетических параметров и характеристик высокоэнергетического лазерного излучения необходимо предусмотреть отсутствие по трассе его распространения газов и паров, которые могут поглощать излучение и приводить к термическим искажениям структуры пучка.
Используемый в измерительной аппаратуре ОЭИП должен обладать высокими разрешающей способностью и отношением сигнал/шум (С/Ш), от которых зависит точность получаемых результатов. Отношение С/Ш играет особую роль при измерениях малых плотностей мощности или энергии (например, в пучках слабоинтенсивного лазерного излучения или же в дифрагировавших частях широкоапертурных пучков). Опыт показывает, что шум в «крыльях» функции распределения E(x, y, z) или H(x, y, z) может заметно доминировать при вычислении моментов второго порядка. Поэтому приходится перекрывать («блокировать») измеряемый пучок, регистрировать распределение плотности мощности (энергии) фонового излучения, а затем вычитать полученные данные из измеренного распределения с «разблокированным» пучком.
Основные требования, предъявляемые к ОЭИП, сводятся к следующему:
· сам ОЭИП и электронная измерительная аппаратура, воспринимающая и преобразующая его выходной сигнал, должны быть линейными; нелинейность, селективность и ЗХ ОЭИП должны быть скорректированы при калибровке аппаратуры;
· ОЭИП должен быть подобран по лучевой стойкости;
· при работе со сканирующим по сечению пучка устройством необходимо обеспечить пространственную и временную стабильность пучка в течение периода сканирования;
· при измерениях пространственно-энергетических параметров и характеристик импульсного лазерного излучения важно согласовать временные параметры импульса с моментом запуска и частотой выборки аппаратуры.
Формирующие, фокусирующие оптические элементы и ослабители не должны искажать распределение интенсивности анализируемого пучка.
Суммарная погрешность, вносимая фокусирующим элементом при измерении расходимости, не должна превышать 1 % от ширины пучка.
18. 1. 4. Измерения ширины и диаметра пучка. Перед началом измерений лазерное устройство должно быть прогрето в течение по крайней мере одного часа (если сертификат изготовителя не содержит других указаний). Далее следует повторить по крайней мере 5 раз измерения функции распределения мощности (энергии) в каждом сечении пучка с координатой z, где определяется его ширина.
Затем с использованием формул (18. 4)—(18. 7) и (18. 17) выполняются соответствующие вычисления. Сначала для каждого измерения определяются моменты первого порядка, затем 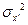 ,
, 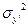 , и
, и  , после чего вычисляются по следующим формулам азимутальный угол φ и ширины пучков
, после чего вычисляются по следующим формулам азимутальный угол φ и ширины пучков 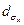 и
и 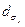 :
:
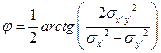 (18. 19)
(18. 19)
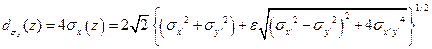 (18. 20)
(18. 20)
где
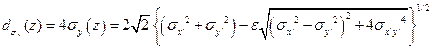 (18. 21)
(18. 21)
 (18. 22)
(18. 22)
Полученные результаты усредняются по количеству выполненных измерений, находятся средние значения и стандартные (средние квадратические) отклонения для ширин пучка и угла φ. Если отношение 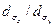 менее, чем 1, 15: 1, то пучок можно считать радиально-симметричным в данном сечении и использовать уравнения (18. 4)—(18. 7) для вычисления не ширины, а диаметра пучка.
менее, чем 1, 15: 1, то пучок можно считать радиально-симметричным в данном сечении и использовать уравнения (18. 4)—(18. 7) для вычисления не ширины, а диаметра пучка.
18. 1. 5. Измерения угла расходимости. Фокусирующий элемент следует расположить таким образом, чтобы его оптическая ось была коаксиаль-на измеряемому лазерному пучку. Затем измерительную плоскость ОЭИП (приемную площадку его чувствительного элемента) разместить на фокусном расстоянии f от задней главной плоскости фокусирующего элемента, после чего выполнить по крайней мере по пяти измерений 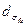 ,
, 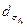 , или
, или 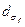 , в этом сечении пучка.
, в этом сечении пучка.
Если пучок радиально-симметричен, то угол расходимости несфокусированного пучка в дальней зоне вычисляется по формуле
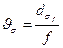 (8. 23)
(8. 23)
где 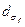 — диаметр пучка в сечении, удаленном на расстояние f от фокусирующего элемента.
— диаметр пучка в сечении, удаленном на расстояние f от фокусирующего элемента.
Затем результаты нескольких измерений усредняются, определяется среднее значение и стандартное (среднее квадратическое) отклонение угла расходимости.
18. 1. 6. Определение совокупности параметров распространения пучка лазерного излучения. Как упоминалось ранее, определение местоположения на оси z перетяжки пучка и ее поперечных размеров требует учета параметров распространения пучка по оптической трассе. Здесь возможны два случая: местоположение перетяжки доступно или нет для прямого измерения. Рассмотрим оба случая.
Если перетяжка пучка доступна для прямого измерения, то ее местоположение и стандартное отклонение определяются путем гиперболической аппроксимации совокупности значений ширины пучка, измеренных в различных его сечениях вдоль оси z. С этой целью измерения производятся по меньшей мере в 10 сечениях вдоль пучка, причем примерно одна половина из них выполняется в пределах рэлеевской длины по любую сторону от перетяжки, а другая — за пределами двойной zR (см. 18. 17).
Для радиально-симметричных пучков используется гиперболическая аппроксимация измеренных значений диаметров:
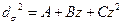 (18. 24)
(18. 24)
После определения коэффициентов Л, В, С гиперболы, путем численной или статистической аппроксимации подходящей кривой (например, путем «взвешивания» результатов отсчета диаметров обратно пропорционально их ] дисперсиям) находятся значения z0 и 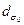 по следующим формулам:
по следующим формулам:
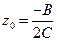 (18. 25)
(18. 25)
 (18. 26)
(18. 26)
Примечание. Для радиально-несимметричных пучков методика измерений и обработки результатов аналогична, но производится по более сложным формулам, приводимым в приложении В к [88].
Если перетяжка пучка не доступна для прямого измерения, то та же методика применима для искусственно формируемой (с помощью безаберрационного фокусирующего элемента) перетяжки. Процедура измерений поясняется рис. 18. 2. Как следует из рис. 18. 2, определению подлежат: расстояние I от фокусирующего элемента до опорной плоскости; расстояние s2 (или s2x и s2y) от искусственно формируемой перетяжки до задней главной плоскости фокусирующего элемента; 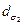 (или
(или 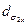 и
и 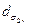 ) в месте расположения искусственно формируемой перетяжки.
) в месте расположения искусственно формируемой перетяжки.
Тогда
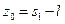 (18. 27)
(18. 27)
где s1 (или же s1x и s1y, согласно приложению В к [88]) определяется как
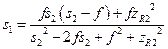 (18. 28)
(18. 28)
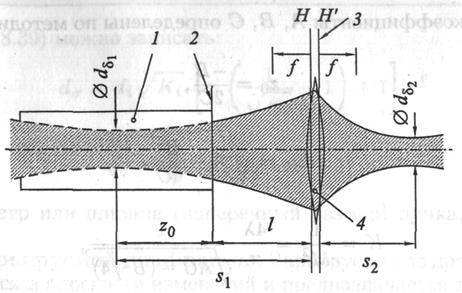
Рис. 18. 2. Вычисление местоположения перетяжки пучка лазерного излучения: 1 — лазер; 2 — опорная (референтная) плоскость; 3 — задняя главная плоскость; 4 — фокусирующий элемент
где f — фокусное расстояние линзы на рис. 18. 2; zR2 — рэлеевская длина для искусственно формируемой перетяжки. Тогда диаметр перетяжки 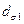 равен
равен
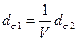 (18. 29)
(18. 29)
где V — увеличение системы.
Если s1 ( 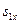 или
или 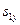 ) равно f, то
) равно f, то
 (18. 30)
(18. 30)
в противном случае
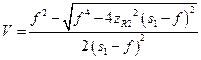 (18. 31)
(18. 31)
18. 1. 7. Определение К или М2. Как упоминалось ранее, для определения К или Μ 2 необходимо измерить диаметр перетяжки и угол расходимости. При этом важно, чтобы измерения угла расходимости выполнялись в той же части пучка, где и ширины перетяжки. Если перетяжка не доступна для прямого измерения, то ее следует искусственно сформировать, и измерения 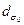 и
и 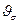 выполнить в одной и той же части пучка.
выполнить в одной и той же части пучка.
По результатам измерений вычисляется
 (18. 32)
(18. 32)
а по стандартным отклонениям результатов измерений 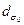 и
и 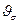 вычисляется стандартное отклонение К(1/М2).
вычисляется стандартное отклонение К(1/М2).
Как и ранее, гиперболическая формула аппроксимации имеет вид
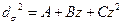 (18. 33)
(18. 33)
Коль скоро коэффициенты А, В, С определены по методике, изложенной в 18. 1. 6, имеем:
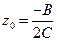 (18. 34)
(18. 34)
 (18. 35)
(18. 35)
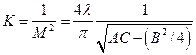 (18. 36)
(18. 36)
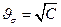 (18. 37)
(18. 37)
 (18. 38)
(18. 38)
18. 1. 8. Альтернативные способы измерений поперечных размеров пучка лазерного излучения. К числу основных причин, по которым не представляется возможным следовать вышеописанным предписаниям и рекомендациям, относятся: трудность или невозможность аппроксимации измеренного распределения плотности мощности (энергии) аналитической функцией; недостаточная разрешающая способность и невысокое отношение С/Ш ОЭИП. С учетом этого в [88] предусмотрены три альтернативных способа измерения ширины пучка и коэффициента К(1/М2). Эти способы основаны на использовании более простой измерительной аппаратуры для определения ширины (поперечных размеров) или диаметра пучка с приемлемой для многих практических случаев точностью.
При этом оказывается справедливым соотношение
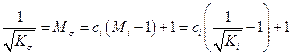 (18. 39)
(18. 39)
где Кi — коэффициент распространения, значение которого найдено i-м альтернативным способом; 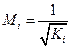 ; Ci — коэффициент корреляции между i-м альтернативным и описанным ранее стандартизованным способом. В [88] рекомендованы следующие альтернативные способы:
; Ci — коэффициент корреляции между i-м альтернативным и описанным ранее стандартизованным способом. В [88] рекомендованы следующие альтернативные способы:
· варьируемой диафрагмы, ci = 1, 14;
· движущегося острого края, сi = 0, 81;
· движущейся щели, Ci = 0, 95.
Следует, однако, учитывать, что приводимые значения Ci проверены и справедливы при выполнении ряда условий, а именно:
· — пучки газовых лазеров с устойчивой геометрией резонаторов и мощностью излучения до 10 Вт; мощность СОг лазеров может достигать 100 Вт; пучки радиально-симметричны; 1  Μ 2
Μ 2  4.
4.
Для лазеров других типов и при М2 > 4 значения Сi должны быть проверены и подтверждены.
С учетом (18. 39) можно записать:
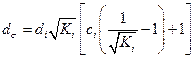 (18. 40)
(18. 40)
или
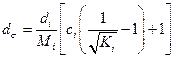 (18. 41)
(18. 41)
где di — диаметр или ширина (поперечный размер) пучка, найденный i-м способом.
Способ варьируемой диафрагмы. Варьируемая по диаметру диафрагма располагается в плоскости измерений и предназначается для определения прошедшей сквозь нее доли мощности (энергии) в функции от ее диаметра. (Нескорректированное значение 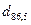 ширины (диаметра) пучка определяется по минимальному диаметру отверстия диафрагмы, сквозь которое проходит 86, 5 % суммарной мощности (энергии) пучка. Способ пригоден лишь для ра-диально-симметричных пучков).
ширины (диаметра) пучка определяется по минимальному диаметру отверстия диафрагмы, сквозь которое проходит 86, 5 % суммарной мощности (энергии) пучка. Способ пригоден лишь для ра-диально-симметричных пучков).
Структурная схема способа поясняется рис. 18. 3.
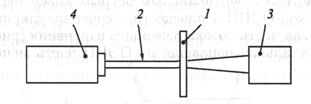
Рис·. 18. 3. Структурная схема способа варьируемой диафрагмы: 1 — варьируемая диафрагма; 2 — пучок лазерного излучения; 3 — ОЭИП; 4 — лазер
К ОЭИП предъявляются те же требования, что описаны в 18. 1. 3. Дополнительным требованием служит «перехват» приемной площадкой чувствительного элемента ОЭИП не менее 99 % суммарной мощности (энергии) излучения.
Диафрагмы следует выбирать по диаметрам таким образом, чтобы при переходе от одной к другой уменьшение мощности (энергии) не превышало 5 %. Допускается также использование калиброванных по диаметру диафрагм.
Сначала ОЭИП устанавливается таким образом, чтобы его главная плоскость была перпендикулярной оси распространения излучения, а центр приемной площадки не был бы смещен относительно оси пучка на расстояние, превышающее 0, 1 ширины пучка. Для центрирования ОЭИП рекомендуется уменьшить диаметр отверстия диафрагмы, чтобы сквозь него проходило около 80% мощности (энергии), после чего перемещать диафрагму в плоскости, перпендикулярной пучку, добиваясь максимального значения выходного сигнала ОЭИП. Далее следует убедиться в том, что на приемную площадку ОЭИП падает вся мощность (энергия) пучка. С этой целью в пучок вблизи приемной поверхности ОЭИП, коаксиально оптической оси, нужно ввести диафрагму таким образом, чтобы она перекрывала порядка 30% периферийной активной площади чувствительного элемента. При этом не должно наблюдаться изменений регистрируемого выходного сигнала ОЭИП, пропорционального суммарной мощности P0 или энергии Q0 лазерного излучения,
Затем следует ступенчато уменьшать диаметр отверстия диафрагмы, но каждый «скачок» должен приводить к сокращению мощности (энергии) пучка, не превышающему 5 %. При этом последовательно регистрируются значения диаметров d1 и d2, причем d1 больше, a d2 меньше диаметра 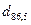 отверстия, сквозь которое проходит 86, 5 % P0 или Q0. Помимо значений d1 и d2 регистрируются и соответствующие значения Р1, P2 или Q1, Q2. Диаметр
отверстия, сквозь которое проходит 86, 5 % P0 или Q0. Помимо значений d1 и d2 регистрируются и соответствующие значения Р1, P2 или Q1, Q2. Диаметр


