 |
Составление дифференциального уравнения движения механизма с помощью теоремы об изменении кинетической энергии
|
|
|
|
Для составления дифференциального уравнения движения механической системы с одной степенью свободы применим теорему об изменении кинетической энергии в дифференциальной форме
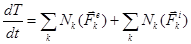 (12)
(12)
где Т - кинетическая энергия системы; 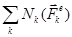 - сумма мощностей внешних сил; -
- сумма мощностей внешних сил; - 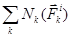 сумма мощностей внутренних сил.
сумма мощностей внутренних сил.
Вычислим кинетическую энергию системы как сумму кинетических энергий тел, образующих механическую систему
Т = Т0+Т1+Т2+Т3+Т4,
где 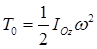 - кинетическая энергия кривошипа ОА, совершающего вращательное движение вокруг оси Oz;
- кинетическая энергия кривошипа ОА, совершающего вращательное движение вокруг оси Oz;
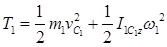 - кинетическая энергия шатуна АB, совершающего плоское движение;
- кинетическая энергия шатуна АB, совершающего плоское движение;
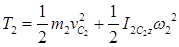 - кинетическая энергия шатуна KD, совершающего плоское движение;
- кинетическая энергия шатуна KD, совершающего плоское движение;
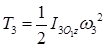 - кинетическая энергия кривошипа О1D, совершающего вращательное движение вокруг оси O1z;
- кинетическая энергия кривошипа О1D, совершающего вращательное движение вокруг оси O1z;
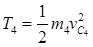 - кинетическая энергия ползуна B, который движется поступательно.
- кинетическая энергия ползуна B, который движется поступательно.
Моменты инерции сплошных однородных стержней, составляющих механизм, относительно осей проходящих через их центры масс равны
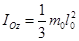
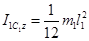
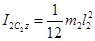
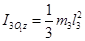
Подставляя всё в выражение кинетической энергии системы, окончательно получаем:
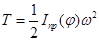 (13)
(13)
где 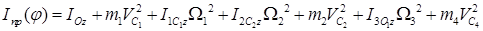 (14)
(14)
- приведенный момент инерции механизма, а величины 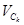 , (k = 1,4) - скорости точек механизма, отнесенные к угловой скорости ведущего звена
, (k = 1,4) - скорости точек механизма, отнесенные к угловой скорости ведущего звена 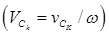
Для рассматриваемой механической системы, состоящей из абсолютно твердых тел, соединенных идеальными шарнирами сумма мощностей внутренних сил равна нулю 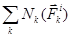 .
.
Сумма мощностей внешних сил будет равна
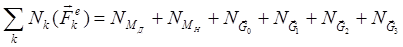
где 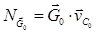 ,
, 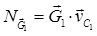 ,
, 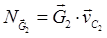 ,
, 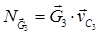 мощности сил тяжести звеньев;
мощности сил тяжести звеньев; 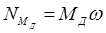 - мощность момента приводящего механизм в движение;
- мощность момента приводящего механизм в движение; 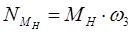 - мощность полезной нагрузки.
- мощность полезной нагрузки.
Мощности сил 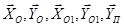 ,
, 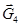 равны нулю, т.к. реакция опорной плоскости YП и сила тяжести
равны нулю, т.к. реакция опорной плоскости YП и сила тяжести 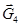 перпендикулярна скорости точки B, а остальные силы приложены к неподвижным точкам.
перпендикулярна скорости точки B, а остальные силы приложены к неподвижным точкам.
|
|
|
Учитывая выражения для движущего момента МД и полезной нагрузки 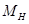 , окончательно получим
, окончательно получим
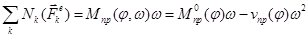 (15)
(15)
где 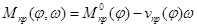 (16)
(16)
- приведенный момент внешних сил, а величины 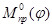 и
и 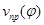 равны
равны
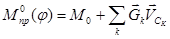

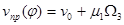
Подставляя найденные выражение кинетической энергии (13) и мощности внешних сил (15) в теорему об изменении кинетической энергии (12), получим дифференциальное уравнение движения механизма
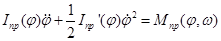 (17)
(17)
где 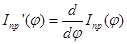 - производная момента инерции механизма по углу поворота ведущего звена.
- производная момента инерции механизма по углу поворота ведущего звена.
Решив данное дифференциальное уравнение второго порядка с указанными в задаче начальными условиями, найдем закон движения ведущего звена 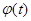 , его угловую скорость
, его угловую скорость 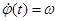 и угловое ускорение
и угловое ускорение 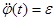 .
.
Нахождение реакций внешних и внутренних связей
Для определения реакций внешних и внутренних связей расчленим плоский шарнирный механизм на отдельные звенья и изобразим реакции внешних и внутренних связей каждого звена (рис. 3).
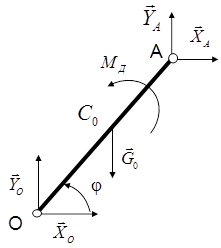
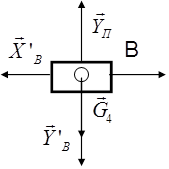
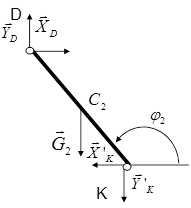
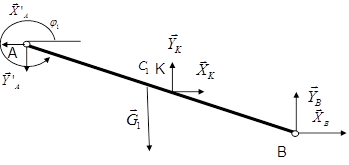
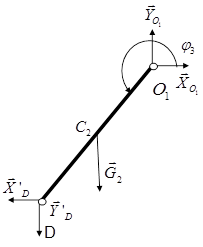
Рис.3 Расчётные схемы звеньев плоского механизма.
Применив к каждому телу, изображенному на расчетной схеме, теорему о движении центра масс (в проекциях на оси координат) и теорему об изменении кинетического момента (для кривошипов относительно осей вращения, для шатунов относительно осей проходящих через центр масс) получим следующую систему уравнений:
Кривошип ОА:
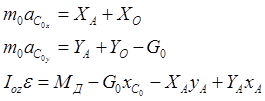 (18)
(18)
Шатун АB:
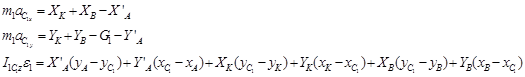 (19)
(19)
Шатун KD:
 (20)
(20)
Кривошип О1D:
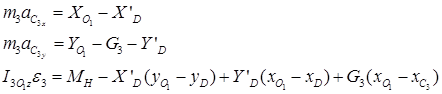 (21)
(21)
Ползун B:
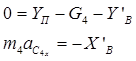 (22)
(22)
Первое уравнение системы (22) позволяет определить реакцию опорной плоскости YП, а третье из системы (18), после подстановки найденных величин, дифференциальное уравнение движения механизма (17).
Оставшиеся двенадцать соотношений представляют собой систему линейных алгебраических уравнений относительно неизвестных реакций.
Результаты расчетов
Решение поставленной задачи сводится к численному интегрированию дифференциального уравнения движения механизма (17) и решению системы двенадцати линейных алгебраических уравнений (18) - (21) относительно неизвестных динамических реакций внешних и внутренних связей.
|
|
|
Задача интегрирования дифференциального уравнения (17) связана с большим количеством предварительных вычислений и может быть условно разбита на пять блоков:
о решение системы уравнений геометрических связей (1) или вычисление геометрических соотношений (2);
о вычисление кинематических соотношений по формулам (3) - (11);
о вычисление приведенного момента инерции механизма и приведенного момента внешних сил.
о вычисление производной от приведенного момента инерции по углу поворота ведущего звена.
о численное интегрирование дифференциального уравнения.
Все это может быть проведено в Mathcad несколькими способами использующими различные встроенные процедуры-функции. Отличие этих способов и методов заключается во времени вычислений, которое требуется для нахождения: решения системы уравнений геометрических связей, приведенного момента инерции механизма и его производной, приведенного момента внешних сил, а также решения дифференциального уравнения движения (17). Ниже рассмотрен алгоритм и приведен документ Mathcad, в котором обеспечивается минимальное время вычислений.
Алгоритм вычислений
Угловые координаты звеньев 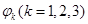 и положение ползуна B
и положение ползуна B 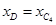 вычисляются в явном виде по формулам (2).
вычисляются в явном виде по формулам (2).
Угловые скорости звеньев 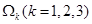 , отнесенных к угловой скорости кривошипа, вычисляются в явном виде по формулам (3).
, отнесенных к угловой скорости кривошипа, вычисляются в явном виде по формулам (3).
Скорости центров масс звеньев 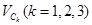 отнесенных к угловой скорости кривошипа, вычисляются в явном виде по формулам (4) - (6), которые примут следующий вид
отнесенных к угловой скорости кривошипа, вычисляются в явном виде по формулам (4) - (6), которые примут следующий вид
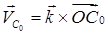
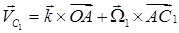
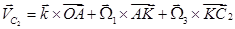
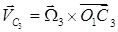 (23)
(23)
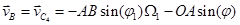
Далее, по формулам (14) и (16) вычисляется приведенный момент инерции 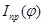 и коэффициенты в приведенном моменте внешних сил
и коэффициенты в приведенном моменте внешних сил 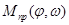 .
.
Для вычисления производной 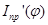 от приведенного момента инерции по углу поворота ведущего звена воспользуемся явным представлением этой производной
от приведенного момента инерции по углу поворота ведущего звена воспользуемся явным представлением этой производной
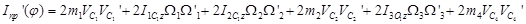 Производные
Производные 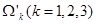 можно найти, продифференцировав по φ систему уравнений
можно найти, продифференцировав по φ систему уравнений 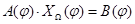 . Получим
. Получим
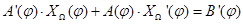
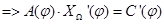
Откуда 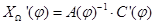 ,
,
где вектор 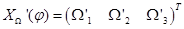 , а матрица
, а матрица 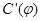 определена соотношением (8).
определена соотношением (8).
Производные 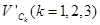 находятся дифференцированием по углу поворота кривошипа ОА выражений (23)
находятся дифференцированием по углу поворота кривошипа ОА выражений (23)
|
|
|
Для численного интегрирования дифференциального уравнения второго порядка (17) представим его в виде системы двух дифференциальных уравнений первого порядка. Введя новые переменные 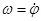 и
и 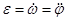 , получим
, получим
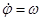
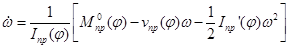 (24)
(24)
Эти соотношения позволяет вычислять угловое ускорение кривошипа, если известны его угол поворота и угловая скорость; в частности, можно вычислить угловое ускорение в начальный момент по заданным начальным значениям угла поворота и угловой скорости кривошипа.
Для интегрирования системы уравнений (24) при заданных начальных условиях используем встроенную в пакет Mathcad процедуру-функцию Radau..
Матрица, получаемая в результате решения, содержит три столбца; первый - для значений времени t, второй - для значений угла поворота 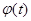 , третий - для значений угловой скорости
, третий - для значений угловой скорости 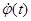
Решение системы линейных алгебраических уравнений (18) - (21), для нахождения динамических реакций внешних и внутренних связей реализуем матричным способом
Ниже приведен документ Mathcad, в котором реализована процедура интегрирования дифференциального уравнения движения механизма и вычисления реакций внешних и внутренних связей.
|
|
|


