Примерный перечень вопросов для подготовки к зачету

 

1. Критерии оценки эффективности инвестиционно-финансовых решений.

2. Формирование инвестиционного портфеля при заданном объёме капиталовложений и наличии производственной программы.

3. Статическая модель синхронизации системы инвестиционного и финансового планирования.

4. Одноступенчатая динамическая модель синхронизации системы инвестиционного и финансового планирования.

5. Многоступенчатая динамическая модель синхронизации системы инвестиционного и финансового планирования.

6. Обоснование целесообразности многокритериального подхода к решению инвестиционных задач.

7. Методы анализа экспертных оценок.

8. Методы определения коэффициентов важности.

9. Многокритериальная модель оптимизации портфеля инвестиций.

10. Обобщённая многокритериальная модель выбора оптимального решения.

11. Аналитическое определение иерархии целей.

12. Планирование на основе метода анализа иерархий.

13. Биномиальные модели ценообразования опционов.

14. Опцион на выход.

15. Опцион на расширение.

16. Опцион на сокращение.

17. Опцион на гибкость.

18. Сложный опцион.

19. Модель Блэка – Шоулза.

20. Дерево решений.

21. Моделирование оптимальных решений в условиях неопределённости.

22. Моделирование оптимальных решений в условиях риска.

23. Комбинированные критерии принятия решений.

24. Модели поведения в условиях конкуренции.

25. Оптимальная схема стимулирования менеджера.

26. Модель устойчивых соглашений.

27. Многокритериальная игра двух лиц.

28. Структура позиционной игры.

29. Нормализация позиционной игры.

30. Позиционные игры с полной информацией.

31. Алгоритм проверки адекватности множественной регрессионной модели (сущность этапов проверки, расчетные формулы, формулировка вывода).

32. Гетероскедастичность случайного возмущения (определение). Алгоритм теста Голдфелда-Квандта на наличие или отсутствие гетероскедастичности случайных возмущений в парной регрессионной модели.

33. Коэффициент детерминации как индикатор качества спецификации эконометрической модели.

34. Модели с бинарными фиктивными переменными.

35. Алгоритм проверки значимости коэффициентов парной регрессионной модели в Excel (с помощью функции «ЛИНЕЙН» или пакета «Анализ данных»). Доверительные интервалы параметров парной регрессионной модели (формулы расчета).

36. Интервальная оценка индивидуального значения зависимой переменной в парной регрессионной модели.

37. Использование фиктивных переменных для определения структурных изменений в экономике.

38. Коэффициент детерминации в множественной регрессионной модели (смысл, расчетная формула). Проверка значимости коэффициента детерминации. Формула расчета и назначение скорректированного коэффициента детерминации в множественной регрессионной модели.

39. Линейная модель множественной регрессии. Порядок её оценивания методом наименьших квадратов в Excel. Смысл выходной статистической информации в Анализе данных.

40. Оценка параметров парной регрессионной модели методом наименьших квадратов с помощью матричных функций в Excel.

41. Понятие о мультиколлинеарности. Методы устранения мультиколлинеарности (перечислить методы, описать любой метод).

42. Фиктивная переменная сдвига: спецификация регрессионной модели с фиктивной переменной сдвига; экономический смысл параметра при фиктивной переменной; смысл названия.

43. Алгоритм теста Дарбина-Уотсона на наличие (отсутствие) автокорреляции случайных возмущений.

44. Измерение тесноты связи между показателями. Анализ матрицы коэффициентов парной корреляции.

45. Использование фиктивных переменных для определения структурных изменений в экономике.

46. Модели нестационарных временных рядов с трендом и сезонной составляющей и их идентификация.

47. Модели уровней временного ряда: мультипликативная, аддитивная, смешанная.

48. Оценивание линейной модели множественной регрессии методом наименьших квадратов (МНК) в Excel с использованием сервиса Поиск решения.

49. Проблема мультиколлинеарности в моделях множественной регрессии. Признаки мультиколлинеарности. Устранение мультиколлинеарности.

50. Спецификация и оценивание МНК эконометрических моделей нелинейных по параметрам.

51. Способы корректировки автокорреляции (авторегрессионные модели первого порядка).

52. Способы корректировки гетероскедастичности. Взвешенный метод наименьших квадратов.

53. Тест Чоу на наличие структурных изменений в регрессионной модели

54. Фиктивная переменная наклона: назначение; спецификация регрессионной модели с фиктивной переменной наклона; значение параметра при фиктивной переменной.

55. Фиктивные переменные: определение, назначение, типы.

 

Примеры задач на зачете

 

Пример 1

Небольшая фирма (игрок A) намерена сбыть партию товара на одном из двух рынков, контролируемых другой, более крупной фирмой (игрок B). Для этого фирма A готова сделать на одном из рынков соответствующие приготовления (например, развернуть рекламную кампанию). Господствующая на рынках фирма B может попытаться воспрепятствовать этому, приняв на одном из рынков предупредительные меры. Не встречая противодействия на рынке, фирма A захватывает его; при наличии препятствий – терпит поражение.

Будем считать для определённости, что проникновение фирмы A на первый рынок более выгодно для неё, нежели на второй. Естественно также считать, что и борьба за первый рынок потребует вложения больших средств. Например, победа фирмы A на первом рынке принесёт ей вдвое больший выигрыш (равный 2), чем победа на втором, но зато и поражение при попытке освоиться на первом рынке полностью её разорит (выигрыш -10), а фирму B избавит от конкурента. Поражение фирмы A на втором рынке принесёт ей проигрыш -1.

При захвате первого или второго рынка фирмой A проигрыши фирмы B по абсолютной величине равны выигрышам фирмы A. Если фирме B удастся отстоять первый рынок, её выигрыш будет равен 5, если второй 1.

У фирмы A две стратегии:

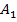– выбор первого рынка;

– выбор второго рынка.

Стратегии фирмы B:

– защита первого рынка;

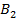– защита второго рынка.

Требуется построить теоретико-игровую модель и найти оптимальные стратегии фирм.

Пример 2

 

Физическое лицо, игрок A, планирует взять кредит в банке, 100 д. е., на срок 1 год под 13%. Для погашения кредита заёмщик рассматривает два варианта действий:

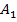– работать на двух работах и отдать весь долг самостоятельно;

– работать на одной работе, успеть отдать в срок самостоятельно только 70 ден. ед. с процентами, оставшуюся сумму занять у «друга» с намерением вернуть ему деньги с дополнительными 14%.

Банк, игрок B, рассматривает варианты поведения:

– за вовремя возвращённый долг вернуть заёмщику 2% выплаченной суммы;

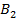– с 80% суммы займа взять 13%, с остальной части долга – только 9%.

Требуется построить теоретико-игровую модель и найти оптимальные стратегии заемщика и банка.

 

Пример 3

Инвестору необходимо принять оптимальное решение, связанное с участием в инвестиционном проекте. Рассматриваются следующие альтернативы финансирования инвестиционного проекта:

− 100%-е финансирование;

− 75%-е финансирование,

− 50%-е финансирование,

− 30%-е финансирование;

− 10%-е финансирование;

− 0%-е финансирование.

Каждая альтернатива предполагает определённую долю участия в проекте. Для упрощения допустим, что доля финансирования соответствует доле чистого дохода, получаемого в результате реализации проекта. Будем предполагать, что средства, соответствующие доле неучастия в проекте, инвестор размещает в банке.

Решение инвестора относительно участия в проекте будет принято с учётом возможных вариантов развития экономической ситуации. Для простоты будем предполагать, что условия реализации проекта будут определяться тремя независимыми факторами:

− объём спроса;

− менеджмент;

− трансакционные издержки.

Обозначим первый фактор символом , второй фактор – , третий – 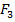. Для количественной оценки влияния каждого фактора на условия реализации проекта будем рассматривать их как переменные бинарного типа. Случаю положительного проявления фактора , i=1,2,3, соответствует некоторая вероятность (, , ).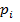

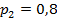Инвестиционный проект требует 100 тыс. условных единиц инвестиций. Известно, что доход проекта при наиболее благоприятных условиях его реализации составит 130 тыс. условных единиц, при наименее благоприятных доход будет равен 80 тыс. Банковская ставка процента равна 8%.

Определить оптимальный вариант участия в проекте с помощью метода утопической точки.

 

Пример 4 4

 

Пусть предприятие имеет пять реальных инвестиционных объектов, характеризующимися приведенными в таблице нетто-платежными рядами. Заданный капитал составляет 340 д.е., расчетная процентная ставка – 10%.

Требуется построить модель синхронного планирования и определить оптимальную инвестиционную программу при заданных ограничениях.

Таблица. Платежные нетто-ряды для пяти инвестиционных объектов и стоимость капитала

Таблица 12

Инвестиционный объект	Нетто-платежы в моменты времени, д.е.	Стоимость капитала, д.е.
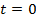
	-90				14,019
					13,858
	-80				10,796
	-170				28,159
	-100				15,251

Пример 5

 

Исследовать динамику экономического показателя на основе анализа одномерного временного ряда.

В течение девяти последовательных недель фиксировался спрос Y(t) (млн. р.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя (повариантно) приведен ниже в таблице

Таблица 13

Номер наблюдения (t = 1,2,…,9)

 

Требуется:

1) Проверить наличие тренда.

2) Построить линейную модель , параметры которой оценить МНК Y (t) - расчетные, смоделированные значения временного ряда:

a) использованием Поиска решений;

b) использованием матричных функций;

c) использованием Анализа данных;

d) использованием Мастера диаграмм.

3) Проверить выполнение свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S-критерия взять табулированные границы 2,7—3,7) и точность модели с помощью средней относительной ошибки аппроксимации.

4) Осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности р = 80%).

5) Построить нелинейные трендовые модели: степенную, гиперболическую и показательную. Привести графики. Выбрать лучшую модель, обосновав выбор.

Пример 6

 

Имеются следующие сведения о количестве пучков салата продаваемого ежедневно в розницу и цене:

Таблица 14

Количество, шт/день
Цена, руб. за единицу

 

Торговцу нужно выяснить, как изменяется количество продаваемого салата при изменении цены.

Требуется:

 

1) построить модель линейной регрессии; дать интерпретацию построенной модели и отдельных ее коэффициентов, оценить точность модели с помощью средней относительной ошибки аппроксимации;

2) если бы цена равнялась 35 руб. за каждый пучок, то, сколько было бы продано салата, (доверительные интервалы прогнозов; рассчитать при уровне значимости, а = 0,2), определить при какой цене продавец не продаст ни одного пучка салата, отобразить на графике фактические данные, результаты моделирования и прогнозирования;

3) построить степенную, гиперболическую и показательную модели; привести их графики, оценить качество.

Пример 7

 

По торговой фирме исследуется влияние стажа работы, уровня образования и пола менеджера по продаже на размер дохода от реализации товаров, принесенного фирме за последний год. Имеются сведения по 10 менеджерам:

 

 

Таблица 15

Менеджер	Доход (млн. руб.)	Стаж (лет)	Образование	Пол
1. Иванова			высшее	женский
2. Петров			среднее	мужской
3. Кузнецов			высшее	мужской
4. Светлова			среднее	женский
5. Сидоренко			высшее	женский
6. Калинин			высшее	мужской
7. Крымова			высшее	Женский
8. Жуков			высшее	мужской
9. Баранова			среднее	женский
10. Семенов			высшее	мужской

Требуется:

 

1. Построить линейную регрессионную модель дохода с полным набором факторов. Оценить параметры модели.

2. Пригодно ли уравнение регрессии для целей анализа и прогнозирования?

3. Существенна ли разница в размере дохода, принесенного менеджерами с высшим и средним образованием?

4. Существенна ли разница в размере дохода, принесенного мужчинами и женщинами?

5. Построить линейную регрессионную модель только со статистически значимыми факторами. Оценить параметры модели. Дать экономическую интерпретацию коэффициентам уравнения регрессии.

6. Оценить точность построенной модели.

7. Спрогнозировать средний доход менеджера с высшим образованием со стажем работы 7 лет.

 

Примечание. Там, где это необходимо, уровень значимости принять равным .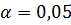

Пример 8

 

Исследуется зависимость цены квартиры от размера ее общей площади, типа дома (кирпичный или панельный) и этажа, на котором расположена квартира (средний или крайний). Имеются данные по 16 квартирам в домах, расположенных в одном и том же районе города:

Таблица 16

№ квартиры	Цена квартиры (долл. США)	Общая площадь ( 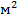)	Тип дома	Этаж
			панельный	крайний
			кирпичный	крайний
			кирпичный	крайний
			панельный	крайний
			кирпичный	средний
			кирпичный	крайний
			кирпичный	крайний
			панельный	средний
			кирпичный	крайний
			кирпичный	средний
			кирпичный	крайний
			панельный	крайний
			кирпичный	средний
			кирпичный	средний
			кирпичный	средний
			панельный	крайний

 

Требуется:

1. Построить линейную регрессионную модель цены квартиры, не содержащую коллинеарных факторов на уровне значимости 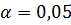. Оценить параметры модели. Значимо ли уравнение регрессии и его коэффициенты на уровне значимости ?

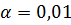2. Какая доля вариации цены квартиры объясняется вариацией факторов, включенных в модель?

3. Приемлема ли точность модели?

4. Что в большей степени влияет на цену квартиры — тип дома или этаж, на котором она расположена? Оценить вклад каждого из факторов в вариацию цены квартиры с помощью дельта – коэффициентов.

5. Спрогнозировать среднюю цену квартиры общей площадью 80 ,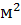

расположенной в панельном доме на одном из крайних этажей.

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: